Representation of data in computer systems Understanding Binary

Representation of data in computer systems Understanding Binary Mr Conti Year 10 Computing 2 nd May 2014

Curriculum Links understand use binary digits, such as to be able to convert between binary and decimal and perform simple binary addition

Learning Objectives By the end of this lesson pupils will have learned: What To the binary number system is. convert between binary and decimal.

Representing data in a computer A computer is an electrical device, so data within a computer can only be represented by electrical signals. These signals have only two states: ON or OFF. Humans use 10 different characters to represent numbers (the decimal system) and 26 characters to represent English words. With just two states, a computer cannot process data in the same way humans would. Computers have to count using the binary system.

Number bases To understand how to count in binary, it is useful to remind ourselves how we count in decimal. The decimal number system counts in groups of 10, or base 10, using the digits 0– 9. Once all the digits have been used, a new column is started that allows higher numbers to be shown with the same digits, for example 10 and 11. Each column has a different weighting, or place value, that represents a different number of tens. For example, the number 1, 234 stands for ‘ 1 thousand, 2 hundreds, 3 tens and 4 units’. Thousands 1 Hundreds 2 Tens 3 Units 4

Base 2 Binary works the same way, but it uses a base of 2 representing electrical ON and OFF signals with the digits 0 and 1. When these two digits have been used up, a new column begins. Decimal 0 1 2 Binary 0 1 10

Base 2 Decimal 0 1 2 3 4 5 Binary 0 1 10 11 0 0 0 1 Number 2 • Can 128 fit into 2 – No • Can 64 fit into 2 – No • Can 32 fit into 2 – No • Can 16 fit into 2 – No • Can 8 fit into 2 – No 6 • Can 4 fit into 2 – No • Can 2 fit into 2 – Yes so it’s a one 7 • Can 0 fit into 1 – No so it’s a zero 8 2 = 10 0

Base 2 Decimal 0 1 2 3 4 5 Binary 0 1 10 11 0 0 0 1 Number 3 • Can 128 fit into 3 – No • Can 64 fit into 3 – No • Can 32 fit into 3 – No • Can 16 fit into 3 – No • Can 8 fit into 3 – No 6 • Can 4 fit into 3– No • Can 2 fit into 3 – Yes so it’s a one 7 • Can 1 fit into 1 – Yes so it’s a one 8 3 = 11 1

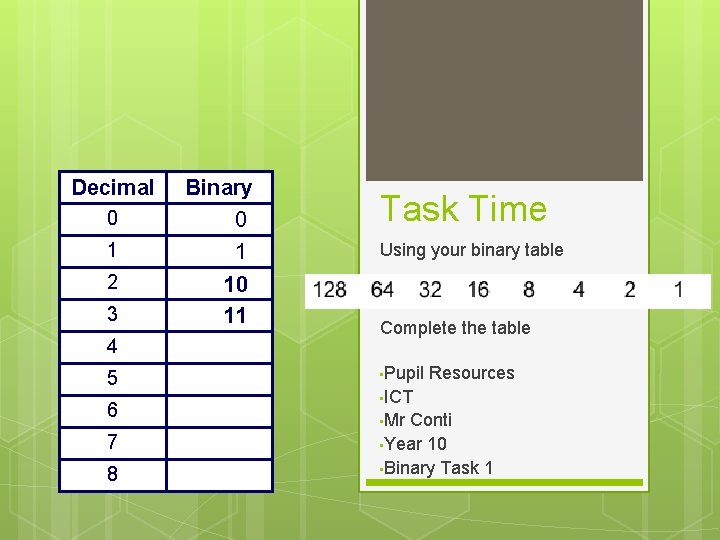
Decimal 0 1 2 3 4 5 6 7 8 Binary 0 1 10 11 Task Time Using your binary table Complete the table • Pupil Resources • ICT • Mr Conti • Year 10 • Binary Task 1

Binary weighting Binary numbers are read in the same way as decimal numbers, but with different values. Each column has a different weighting, just like base 10, but instead of being worth 10 times as much as the previous column, each column in binary is twice as large as the one before. What is the decimal equivalent of the binary number 1011? 8 1 4 0 2 1 Units 1 1 eight + 1 two + 1 unit = 11.

Task Time • Pupil Resources • ICT • Mr Conti • Year 10 • Image Representation Task JUST COMPLETE THE TASKS!!!