Representation and compression of strings Strings sequences of

Representation and compression of strings • Strings - sequences of symbols drawn from a character set, 1) can be the set of alphanumeric characters, punctuators and spaces, and strings are text files 2) can be the quantized intensity levels of pixels in an image, and strings could be digital representation of images (row major order, for example)

Basic problems in string processing • Representing strings • Storage and communication efficiency – how do we assign bit strings to elements of the alphabet to obtain compact, encoded strings? • Exact versus approximate representations • For text data, we probably want representations that decode exactly. • But for data like images or sound files, it might be sufficient to have representations that decode only approximately. • Distinction made between lossless and lossy compression.

String problems • String matching – given a long text string and a pattern, determine if the pattern occurs in the string • Might want all occurrences.

String encodings • The bit sequence representing a symbol from a character set is called its encoding • • ASCII is a common encoding for alphanumeric strings General problem: Given a string t (called the text) over , store it using as few bits as possible.

Huffman encoding • Can use a straightforward encoding of symbols 1) suppose size of is n 2) then represent each symbol in using a b = roof[logn] bit string 3) Then a string of length n will require bn bits to encode

Huffman encoding • Suppose that we use bit sequences of different lengths to represent different symbols 1) symbols that appear frequently will be represented using short sequences 2) symbols that appear rarely will be encoded using long sequences

Huffman encoding Sequences have to be defined so that they cannot be confused! • Example of poorly designed sequences: • 1) E = 101 2) T = 110 3) Q = 101110 • How could we distinguish between the encoding of ET and Q?

Huffman encoding • Solution: No bit sequence used to encode a symbol may be the prefix of the encoding of another symbol • so if the next k bits of the input matches the encoding for a given symbol, then that symbol must be the next symbol

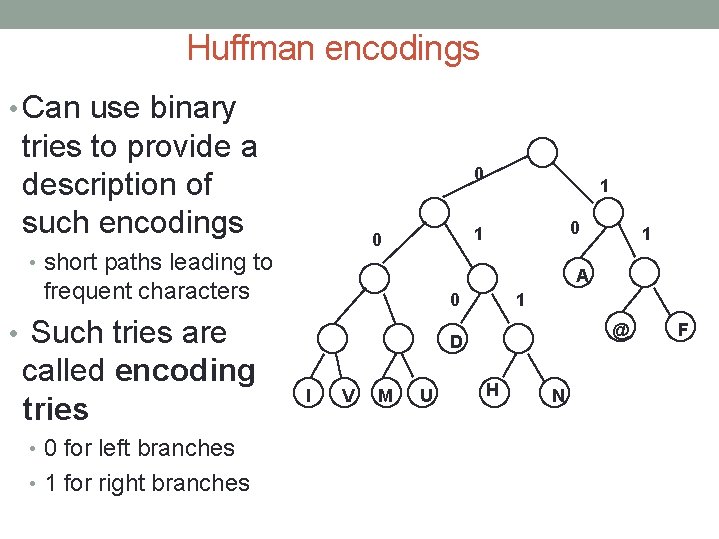
Huffman encodings • Can use binary tries to provide a description of such encodings 0 0 • Such tries are • 0 for left branches • 1 for right branches 1 A frequent characters called encoding tries 0 1 0 • short paths leading to 1 1 @ D I V M U H N F

Huffman encodings • Encoding a string, t, is easy - just concatenate the bit sequence that encodes each symbol. • I FIV = 0000001011100000001 • Decoding is also easy 1) start at the root and move down the trie using the bits from t', the encoding of t, to determine path 2) When a leaf is reached, output the character and return to the root. • Big question - how should the trie be constructed to provide the most efficient encoding?

Huffman encodings • Suppose we want to develop the best encoding (build the encoding trie) for a fixed string t • t might be the string corresponding to the text of the Encyclopedia Britannica • Let fi be the number of times that symbol ci occurs in t • fi is related to the probability that a random symbol chosen from t will be ci.

Huffman encoding • We start by assigning one node to each symbol in . Each of these nodes will be a leaf of the encoding trie, T. • each node has a field to store its weight. Initially, the weight of the node for ci is fi.

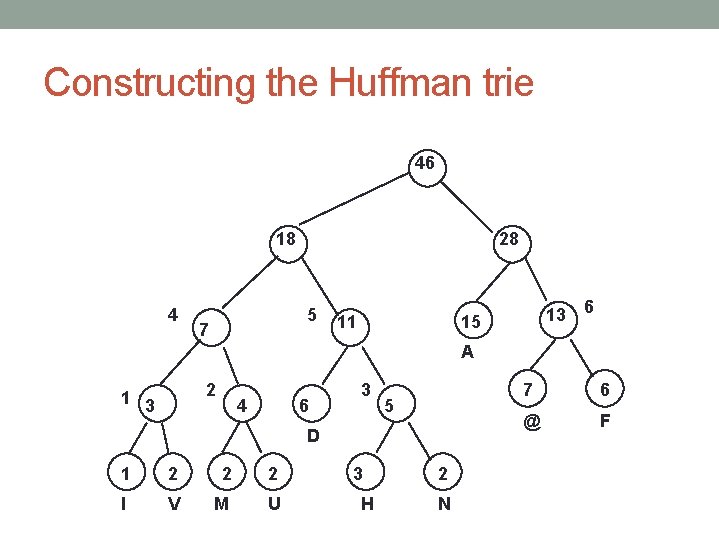
The magic of Huffman encodings • Repeatedly perform the following step: • Pick two nodes, n 1 and n 2, having smallest weights (it doesn't matter how ties are broken) • Make a new node corresponding to the father of n 1 and n 2. The weight of this new node is the sum of the weights of n 1 and n 2. • Nodes n 1 and n 2 are marked as used, and will not participate in further merging - so we reduce the number of active nodes at each step by 1. • Eventually only a single node is left - it is the root of the encoding tree. • The trie constructed is called the Huffman encoding trie.

Constructing the Huffman trie 46 18 4 28 5 7 11 13 15 6 A 2 1 3 4 6 3 5 D 1 2 2 2 I V M U 3 H 2 N 7 6 @ F

Extensions • Biggest problem with Huffman algorithm is that all character frequencies must be known in advance - must read t twice - once to build T and second time to encode it - not always feasible to do this • Static Huffman encoding - fix a single encoding trie, and use it for many texts • Many English texts have similar symbol frequencies

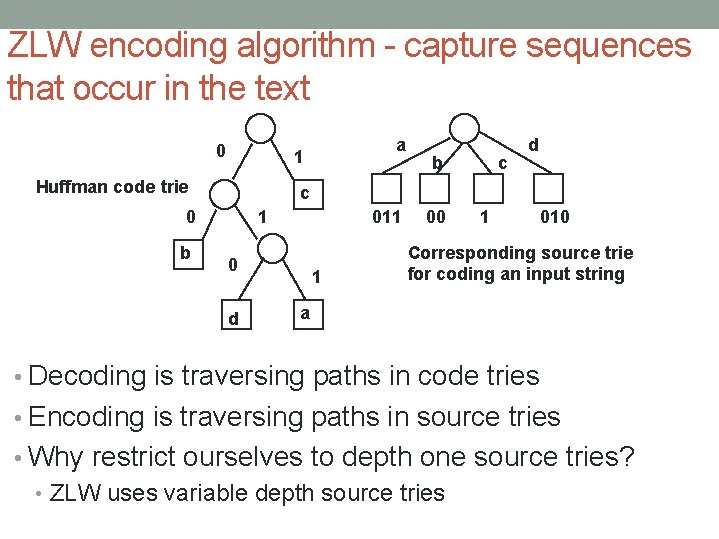
ZLW encoding algorithm - capture sequences that occur in the text 0 Huffman code trie b c d c 0 b a 1 1 011 0 d 1 00 1 010 Corresponding source trie for coding an input string a • Decoding is traversing paths in code tries • Encoding is traversing paths in source tries • Why restrict ourselves to depth one source tries? • ZLW uses variable depth source tries

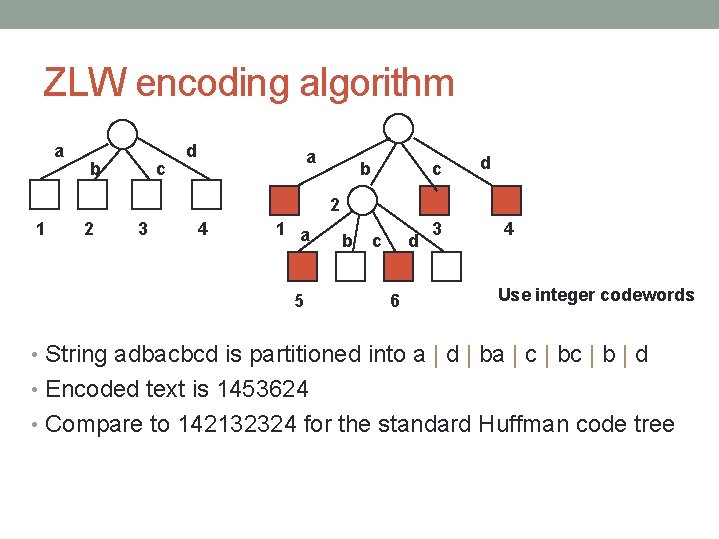
ZLW encoding algorithm a b c d 2 1 2 3 4 1 a 5 b c d 6 3 4 Use integer codewords • String adbacbcd is partitioned into a | d | ba | c | b | d • Encoded text is 1453624 • Compare to 142132324 for the standard Huffman code tree

ZLW encoding • Source tries do not satisfy the prefix property • But we can use them as long as we employ a Greedy partitioning strategy • continue extending a root to frontier path as long as we can • that is why we treat ba as ba rather than a b followed by an a • For ZLW both the source tokens and codewords are variable length • tokenizing - partitioning of the source text into tokens before encoding them • In our examples the codes will be integers - but they can in turn be represented by variable length bit strings

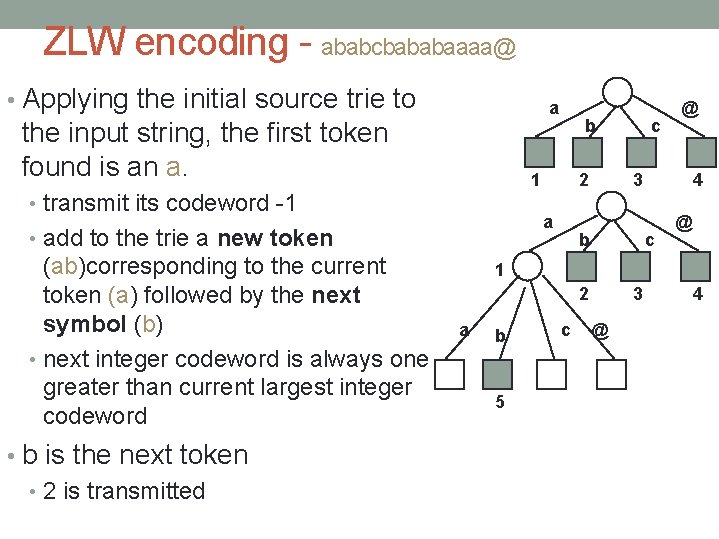
ZLW encoding • With prefix codes we assume that encoder and decoder know the code before the source text is encoded • ZLW - encoder and decoder know the source alphabet and its encoding as integers • Source trie is initialized by both encoder and decoder as a height one trie with one leaf for each alphabet symbol • Example string - ababcbababaaaa@ • source alphabet is {a, b, c, @} • Trie will be grown by extending each 1 matched path (token) by one symbol a b 2 c 3 @ 4

ZLW encoding - ababcbababaaaa@ • Applying the initial source trie to a the input string, the first token found is an a. 1 • transmit its codeword -1 • b is the next token • 2 is transmitted 2 a • add to the trie a new token (ab)corresponding to the current token (a) followed by the next symbol (b) • next integer codeword is always one greater than current largest integer codeword b c @ 3 b 4 c @ 1 2 a b 5 c 3 @ 4

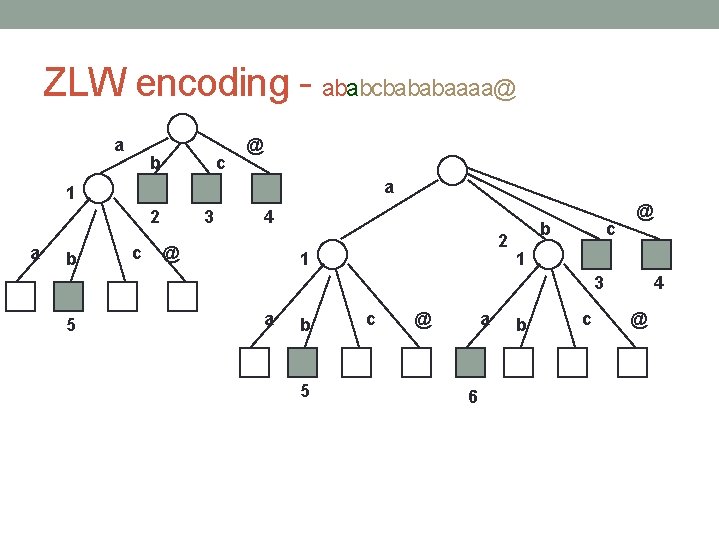
ZLW encoding - ababcbababaaaa@ a b c @ a 1 2 a b c 3 4 @ 2 1 b c @ 1 3 5 a b 5 c @ a 6 b c 4 @

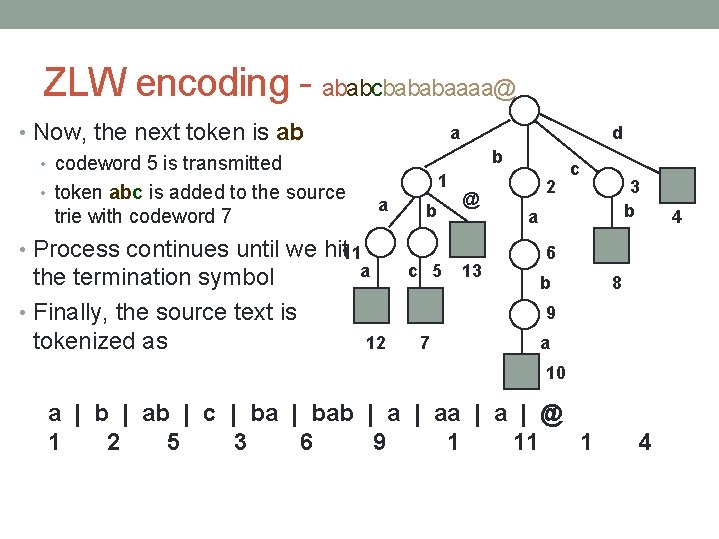
ZLW encoding - ababcbababaaaa@ • Now, the next token is ab • codeword 5 is transmitted • token abc is added to the source trie with codeword 7 a b 1 a • Process continues until we hit 11 the termination symbol • Finally, the source text is tokenized as d a b c 5 @ 13 2 c 3 b a 4 6 b 8 9 12 7 a 10 a | b | ab | c | bab | aa | @ 1 2 5 3 6 9 1 11 1 4

ZLW decoding algorithm • Can the receiver build the source trie as codes are received and decode the text? • Decoder begins with the same initial source trie defined over only the alphabet of individual symbols • It then reconstructs the same sequence of source tries that the encoder produces. • Assume that decoder has accomplished this for a nonempty prefix of the encoded text that ends with the code integer, i, and that the next integer received is j. Two cases: • j is already in the source trie • j is not already in the source trie

• Let the token corresponding to i be x, which by assumption is in the source trie • Suppose j is in the source trie • Let its corresponding token be ay for some symbol a and string y. • Then the encoder would have processed xay and would have added the token xa to its source trie with the next integer as its codeword • So, decoder also adds xa to its source trie

ZLW decoding algorithm a • source trie after encoding abab. . . • decoder has seen 1|2 and has created same source trie • encoder them emits 5 • decoder knows that ab is next matching token; this begins with a • so, decoder adds ba to source trie - previous token followed by first b c @ 1 2 b 5 3 4

ZLW decoding algorithm • But what if j is not in the source trie? • This can only occur if j is a token of the form dx’d where x = dx’. • j must begin and end with the same symbol as the previous token • So, decoder adds the token dx’d to the source trie with integer codeword j.

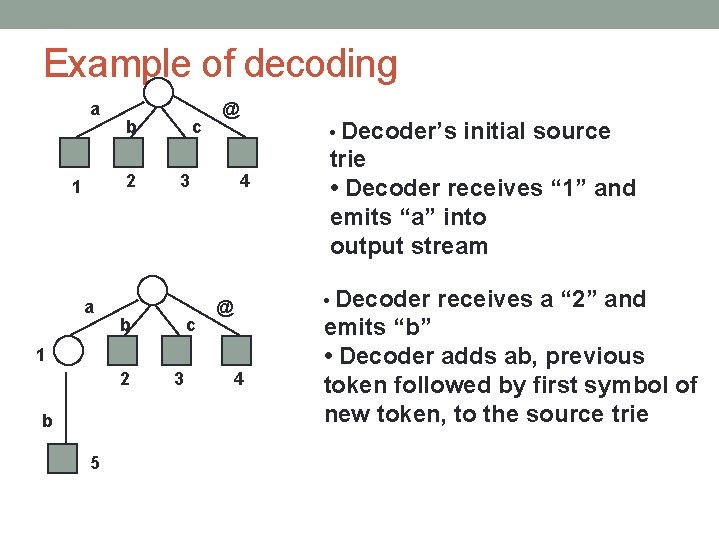
Example of decoding a b 2 1 a c @ 3 b c • Decoder’s 4 1 2 b 5 3 trie • Decoder receives “ 1” and emits “a” into output stream • Decoder @ 4 initial source receives a “ 2” and emits “b” • Decoder adds ab, previous token followed by first symbol of new token, to the source trie

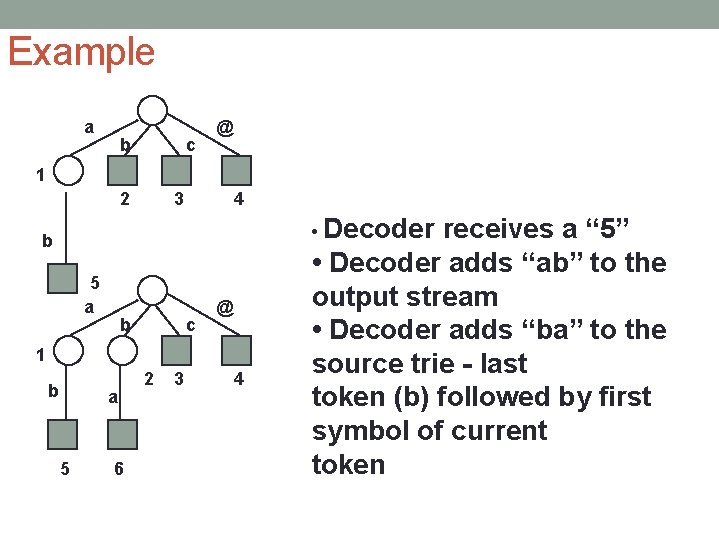
Example a b c @ 1 2 3 4 • Decoder b 5 a b c @ 1 b a 5 6 2 3 4 receives a “ 5” • Decoder adds “ab” to the output stream • Decoder adds “ba” to the source trie - last token (b) followed by first symbol of current token

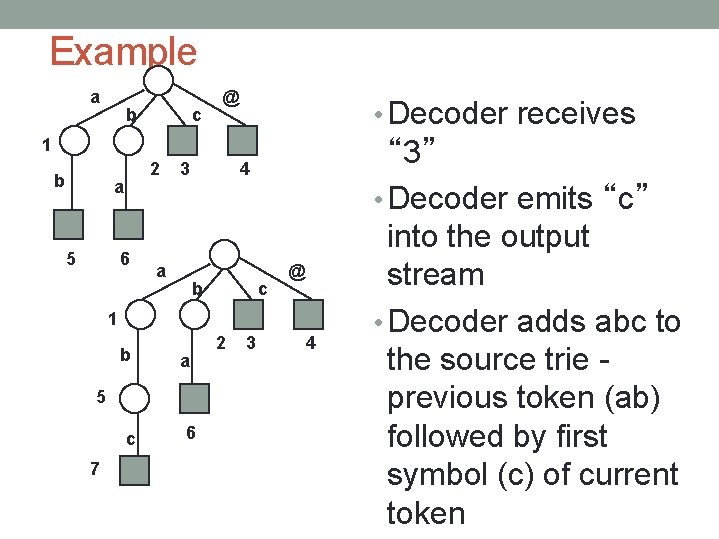
Example a b c @ • Decoder receives 1 b 2 a 5 6 3 a 4 b c @ 1 b a 5 c 7 6 2 3 4 “ 3” • Decoder emits “c” into the output stream • Decoder adds abc to the source trie previous token (ab) followed by first symbol (c) of current token

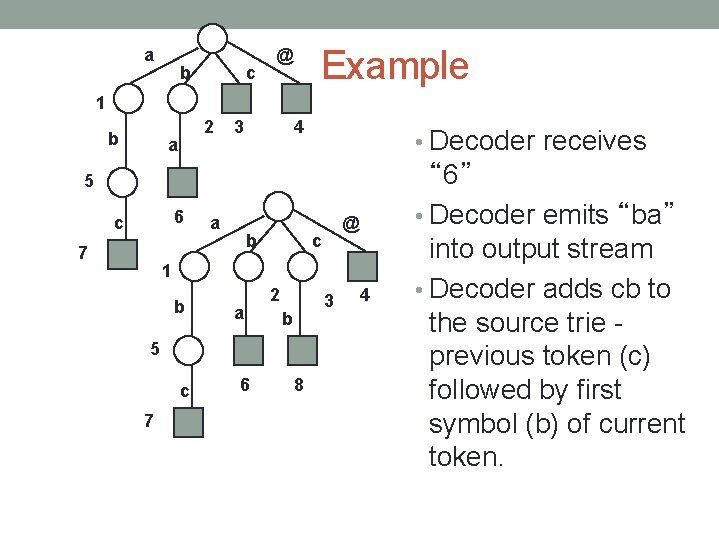
a b c Example @ 1 b 2 a 3 4 • Decoder receives 5 6 c 7 a b @ c 1 b a 2 3 b 5 c 7 6 8 4 “ 6” • Decoder emits “ba” into output stream • Decoder adds cb to the source trie previous token (c) followed by first symbol (b) of current token.

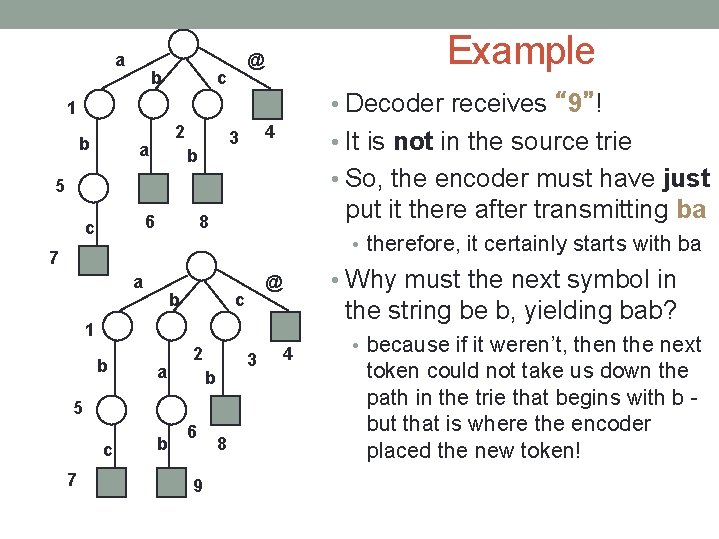
a b Example @ c • Decoder receives “ 9”! 1 b 2 a 4 3 b • It is not in the source trie • So, the encoder must have just 5 6 c put it there after transmitting ba 8 • therefore, it certainly starts with ba 7 a b • Why must the next symbol in @ c the string be b, yielding bab? 1 b a c b 2 3 b 5 7 6 9 8 4 • because if it weren’t, then the next token could not take us down the path in the trie that begins with b but that is where the encoder placed the new token!

Implementation of the source trie at the decoder • Don’t need to use a tree structure to represent the trie at the decoder • Sufficient to have a table indexed by codeword • Each table entry could contain the token corresponding to that codeword. • But then we would need to allocate large amounts of storage to each entry in the table, since the tokens can get long • Instead, can store the last symbol and the codeword for the prefix of the token • this prefix must be in the table since we have a trie.