Representation and Compression of MultiDimensional Piecewise Functions Dror

Representation and Compression of Multi-Dimensional Piecewise Functions Dror Baron Signal Processing and Systems (SP&S) Seminar June 2009 Joint work with: Venkat Chandrasekaran Michael Wakin Richard Baraniuk

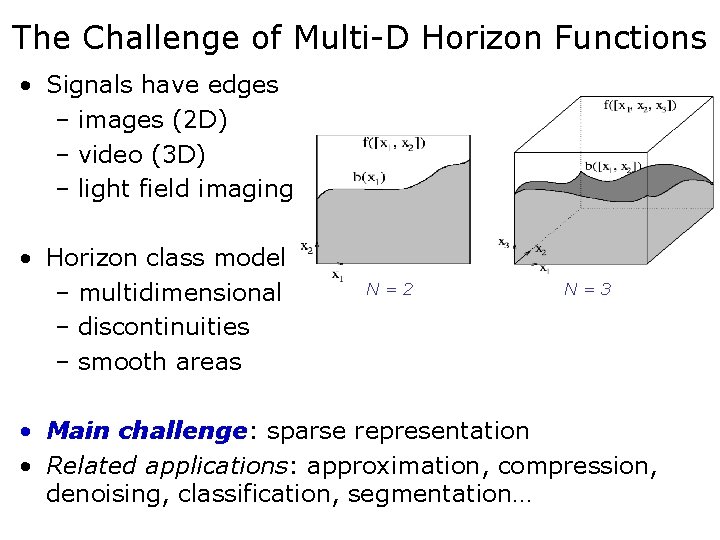
The Challenge of Multi-D Horizon Functions • Signals have edges – images (2 D) – video (3 D) – light field imaging (4 D, 5 D) • Horizon class model – multidimensional – discontinuities – smooth areas N=2 N=3 • Main challenge: sparse representation • Related applications: approximation, compression, denoising, classification, segmentation…

Existing tool: 1 D Wavelets • Advantages for 1 D signals: – efficient filter bank implementation – multiresolution framework – sparse representation for smooth signals • Success motivates application to 2 D, but…

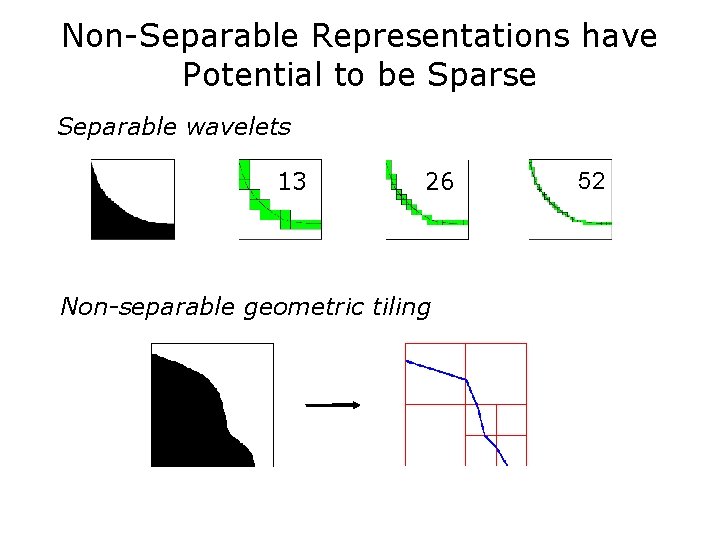
2 D Signal Representations • Challenge: geometry - discontinuities along 1 D contours – separable 2 D wavelets (squares) fail to capture geometric structure 13 26 52 • Response: – tight frames: curvelets [Candés & Donoho], contourlets [Do & Vetterli], bandelets [Mallat] – geometric tilings: wedgelets [Donoho], wedgeprints [Wakin et al. ]

Wedgelet Dictionary [Donoho] • Piecewise linear, multiscale representation – supported over a square dyadic block wedgelet decomposition • Tree-structured approximation • Intended for C 2 discontinuities

Non-Separable Representations have Potential to be Sparse Separable wavelets 13 26 Non-separable geometric tiling 52

Signal Representations in Higher Dimensions • Failure of separable wavelets more pronounced in N>2 dimensions • Similar problems exist – smooth regions separated by discontinuities – discontinuities often smooth functions in N-1 dimensions • Shortcomings of existing work – not yet extended to higher dimensions – intended for efficient (sparse) representations for C 2 discontinuities

Goals • Develop representation for higher-dimensional data containing discontinuities – smooth N-dimensional function – (N-1)-dimensional smooth discontinuity • Optimal rate-distortion (RD) performance – metric entropy – order of RD function • Flow of research: – From N=2 dimensions, C 2 -smooth discontinuities – To N¸ 2 dimensions, arbitrary smoothness

Piecewise Constant Horizon Functions [Donoho] • f: binary function in N dimensions • b: CK smooth (N-1)-dimensional horizon/boundary discontinuity • Let x 2 [0, 1]N and y = {x 1, …, x. N-1} 2 [0, 1](N-1)

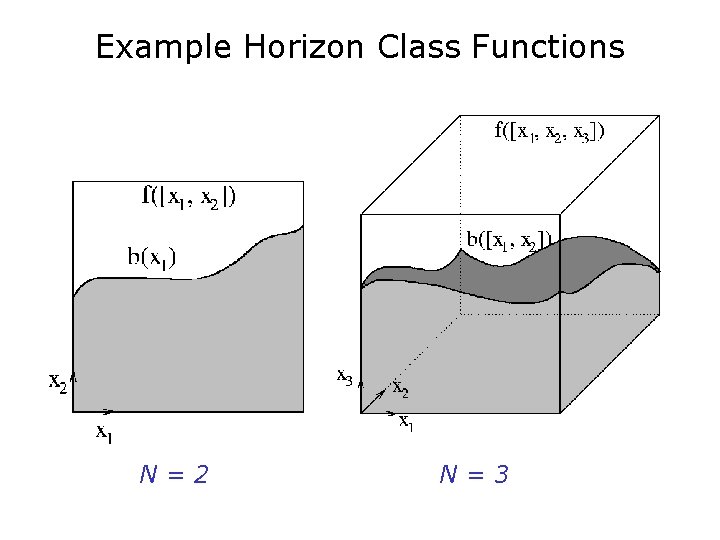
Example Horizon Class Functions N=2 N=3

Compression Problem • Approximate f with R bits ! • Squared L 2 error metric (energy) • Need optimal tradeoff between rate and L 2 distortion

Compression via Implicit Approximation • Edge detection: – estimate horizon discontinuity b – encode using (N-1)-dimensional wavelets [Cohen et al. ] • Implicitly approximate f from b • Theorem [Kolmogorov & Tihomirov; Clements]: Metric entropy for CK smooth (N-1)-D function: L 1 distortion O(¢) lower bound

Metric Entropy for Horizon Functions • Problems with edge detection: – edge detection often impractical – want to approximate f (not b) require solution that provides estimate in Ndimensions, without explicit knowledge of b • Theorem: Metric entropy for N-D horizon function f with CK smooth (N-1)-D discontinuity: • Converse result – our algorithms achieve this RD performance

Motivation for Solution: Taylor’s Theorem • For a CK function b in (N-1) dimensions, derivatives • Key idea: order (K-1) polynomial approximation on small regions • Challenge: organize tractable discrete dictionary for piecewise polynomial approximation

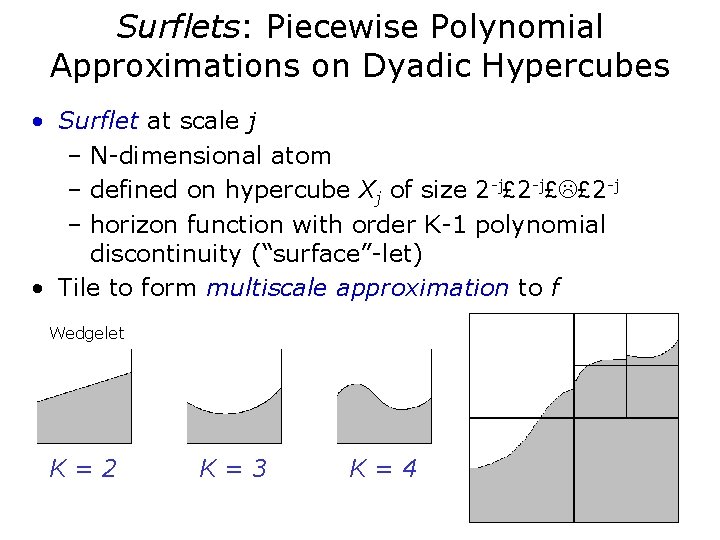
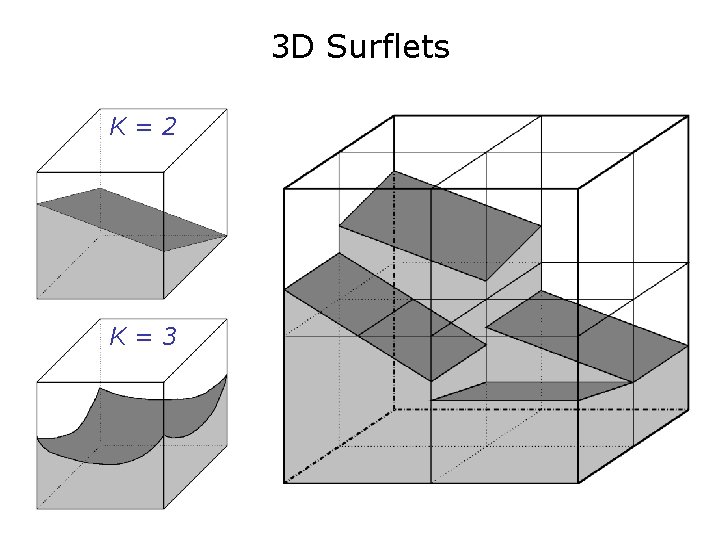
Surflets: Piecewise Polynomial Approximations on Dyadic Hypercubes • Surflet at scale j – N-dimensional atom – defined on hypercube Xj of size 2 -j£L£ 2 -j – horizon function with order K-1 polynomial discontinuity (“surface”-let) • Tile to form multiscale approximation to f Wedgelet K=2 K=3 K=4

3 D Surflets K=2 K=3

Discrete Surflet Dictionary • Describe surflet using polynomial coefficients Wedgelet K=2 K=3 K=4 K=2 K=3

Quantization • Challenge: with naïve quantization of coefficients, dictionary size blows up with K and N • Surflet coefficients approximate Taylor coefficients ~ O(2 -(K-2)j) ~ O(2 -Kj) ~ O(2 -2 j) ~ O(2 -Kj) • Higher-order coefficients quantized with lesser precision same order error for all coefficients • Response: for order-l coefficient, use step-size

Approximation without Edge Detection • “Taylor surflets” – obtained by quantizing derivatives of b – requires knowledge/estimation of b • “L 2 -best surflets” – obtained by searching dictionary for best fit – requires no explicit knowledge of b – fast search algorithm via manifolds • Theorem: Taylor or L 2–best surflets have same asymptotic performance

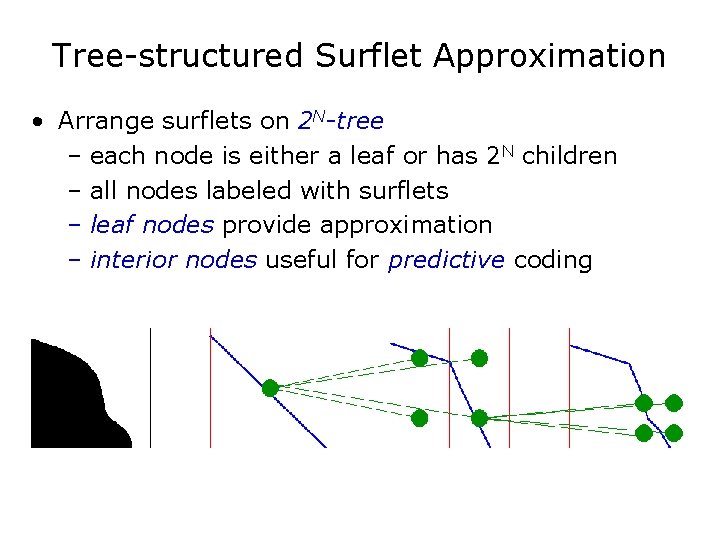
Tree-structured Surflet Approximation • Arrange surflets on 2 N-tree – each node is either a leaf or has 2 N children – all nodes labeled with surflets – leaf nodes provide approximation – interior nodes useful for predictive coding

Tree-structured Surflet Encoder • Surflet leaf encoder achieves near-optimal RD performance • Top-down predictive encoder – code all nodes in surflet tree – use parent surflets to predict children – constant # bits per surflet regardless of scale – layered coarse-scale approximation in early bits • Theorem: Top-down predictive encoder achieves

Discretization • Signals often acquired discretely (pixels/voxels) Pixelization artifacts at fine scales • Approach to discrete data – discretize continuous surflet dictionary – coarse scales: use regular dictionary – smaller dictionary at fine scales • Theorem: Predictive encoder achieves same RD performance at low rate with discretized dictionary

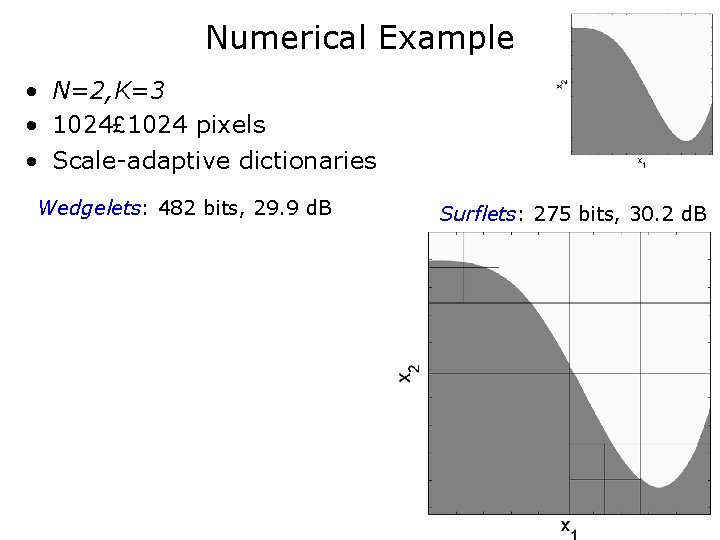
Numerical Example • N=2, K=3 • 1024£ 1024 pixels • Scale-adaptive dictionaries Wedgelets: 482 bits, 29. 9 d. B Surflets: 275 bits, 30. 2 d. B

RD Results • Dictionary 1: fixed-scale wedgelets • Dictionary 2: wedgelets + scale-adaptive • Dictionary 3: surflets + scale-adaptive

Piecewise Smooth Horizon Functions g 1([x 1, x 2]) • g 1, g 2: real-valued smooth functions – N dimensional – CKs smooth • b: CKd smooth (N-1)-dimensional horizon/boundary discontinuity b(x 1) g 2([x 1, x 2]) • Theorem: Metric entropy for CKs smooth N-D horizon function f with CKd smooth discontinuity:

Surfprints • Challenge: – wavelets good in smooth regions – wavelets wasteful near discontinuity 13 26 52 • Surflets good near edges • Response: surfprints project surflets to wavelet subspace

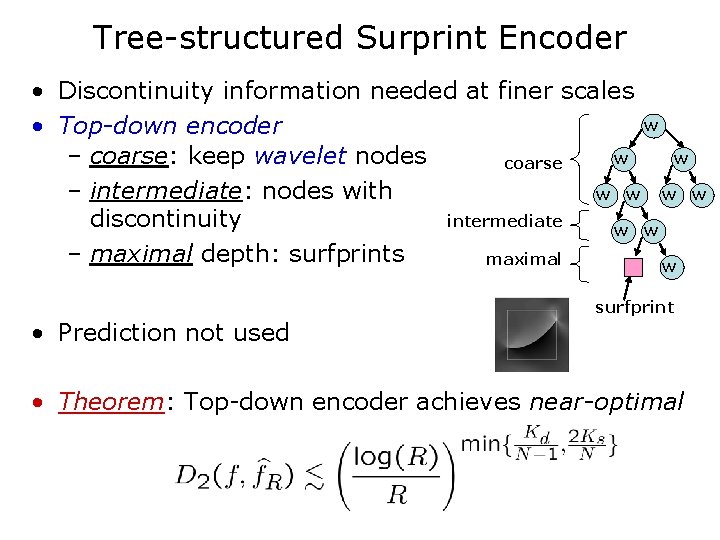
Tree-structured Surprint Encoder • Discontinuity information needed at finer scales w • Top-down encoder – coarse: keep wavelet nodes w w coarse – intermediate: nodes with w w intermediate discontinuity w w – maximal depth: surfprints maximal w • Prediction not used surfprint • Theorem: Top-down encoder achieves near-optimal

Conclusions and Future Work • Metric entropy (converse) – piecewise constant/smooth horizon functions – arbitrary dimension & arbitrary smoothness • Multiresolution compression framework (achievable) – quantization scheme tractable dictionary size – predictive top-down coding optimal performance – scale-adaptive approach to discretization – surfprints at maximal depth near-optimal • Future research: algorithms

THE END