Representacin de sistemas lineales en forma matricial Axb

Representación de sistemas lineales en forma matricial Ax=b

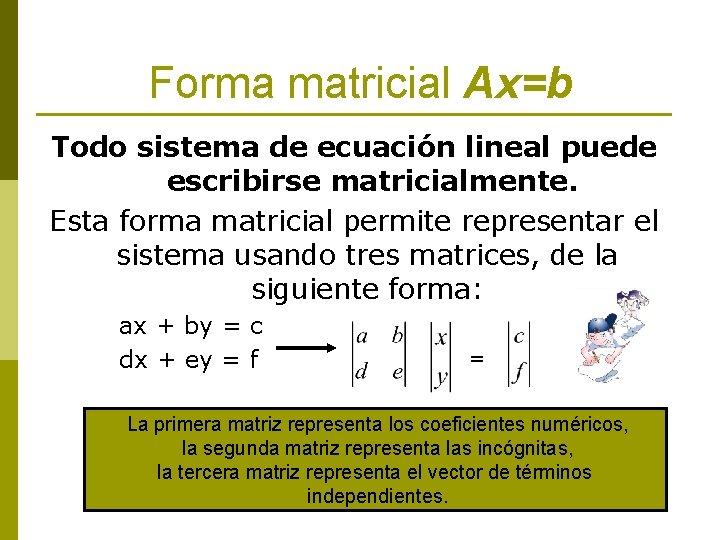
Forma matricial Ax=b Todo sistema de ecuación lineal puede escribirse matricialmente. Esta forma matricial permite representar el sistema usando tres matrices, de la siguiente forma: ax + by = c dx + ey = f = La primera matriz representa los coeficientes numéricos, la segunda matriz representa las incógnitas, la tercera matriz representa el vector de términos independientes.

Representa un sistema de ecuaciones en ecuación matricial (Ax=b) La suma de los dígitos de un numero de dos cifras es 10 y el número que se obtiene al intercambiar los dígitos es 18 menos que el número original. x + y = 10 La suma de los dígitos 10 x + y = 10 y + x – 18 El numero que se obtiene al intercambiar dígitos es 18 menos que el original El sistema se transforma en: x + y = 10 9 x – 9 y = -18 Representación matricial Ax=b =

Representación de ejemplos lección 1 La suma de dos números es 35. Cuatro veces el primero es tres veces el segundo. x + y = 35 4 x = 3 y (la igualamos a cero) El sistema se transforma: x + y = 35 4 x – 3 y = 0 Representación matricial Ax=b = 4 x – 3 y = 0

Representación de ejemplos lección 1 Kary compró 20 sellos, algunos a $. 30 y otros a $. 20. En total pagó $5. 50 Sistema de ecuación lineal: x + y = 22 20 x + 30 y= 550 Representación matricial Ax=b =