Replicated Latin Squares n Three types of replication

Replicated Latin Squares n Three types of replication in traditional (1 treatment, 2 blocks) latin squares – Case study (s=square, n=# of trt levels) n Crossover designs – Subject is one block, Period is another – Yandell introduces crossovers as a special case of the split plot design

Replicated Latin Squares-Case 1 n Column=Operator, Row=Batch n Case 1: Same Operator, Same Batch Source Treatment Batch Operator Rep Error Total df n-1 n-1 s-1 By subtraction sn 2 -1

Replicated Latin Squares-Case 2 n Case 2: Different Operator, Same Batch Source Treatment Batch Operator O(S) Square Error Total df n-1 sn-1 s(n-1) s-1 By subtraction sn 2 -1

Replicated Latin Squares-Case 3 a n Case 3: Different Operator, Different Batch Source Treatment Batch Operator Error Total df n-1 sn-1 By subtraction sn 2 -1

Replicated Latin Squares-Case 3 b n Case 3: Different Operator, Different Batch n Montgomery’s approach Source Treatment Batch(Square) Operator(Square) Square Error Total df n-1 s(n-1) s-1 By subtraction sn 2 -1

Crossover Design n Two blocking factors: subject and period n Used in clinical trials 1 Period 1 A Period 2 B 2 A B Subject 3 4 B A A B 5 B A 6 B A

Crossover Design as Replicated Latin Square n Rearrange as a replicated Latin Square 1 Period 1 A Period 2 B 3 B A Subject 2 5 A B B A 4 A B 6 B A

Crossover Designs n Yandell uses a different approach, in which – Sequence is a factor (basically the WP factor) – Subjects are nested in sequence Period 1 Period 2 Period 3 1 A B C 2 B C A 3 C A B 4 C B A 5 A C B 6 B A C

Crossover Designs-Yandell n Yandell uses a different approach, in which – Period is an effect (I’d call it a common SP) – Treatment (which depends on period and sequence) is the Latin letter effect (SP factor) – Carryover is eventually treated the same way we treat it

Crossover Designs Notes n The replicated Latin Square is an artifice, but helps to organize our thoughts n We will assume s Latin Squares with sn subjects n If you don’t have sn subjects, use as much of the last Latin Square as possible

Crossover Designs-Example n Example (n=4, s=2) Period 1 Period 2 Period 3 Period 4 1 A B C D 2 B C D A 3 C D A B 4 D A B C 5 A B C D 6 B C D A 7 C D A B 8 D A B C

Crossover Designs-Case 2 n This is similar to Case 2 n The period x treatment interaction could be separated out as a separate test – Block x treatment interaction n Periods can differ from square to square-- this is similar to Case 3

Carry-over in Crossover Designs n Effects in Crossover Designs are confounded with the carry-over (residual effects) of previous treatments n We will assume that the carry-over only persists for the treatment in the period immediately before the present period

Carry-over in Crossover Designs-Residual Treatment n In this example, we observe the sequence AB, but never observe BA 1 2 3 Period 1 A B C Period 2 B C D Period 3 C D A Period 4 D A B C 5 A B C D 6 B C D A 7 C D A B 8 D A B C

Carry-over in Crossover Designs-Balance n A crossover design is balanced with respect to carry-over if each treatment follows every other treatment the same number of times n We can balance our example (in a single square) by permuting the third and fourth rows

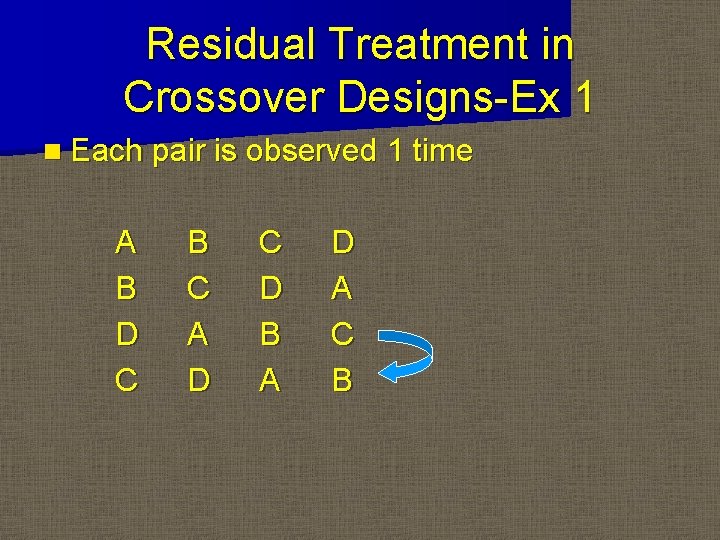
Residual Treatment in Crossover Designs-Ex 1 n Each pair is observed 1 time A B D C B C A D C D B A D A C B

Residual Treatment in Crossover Designs-Ex 2 n For n odd, we will need a replicated design A B C A C A B A C B B A C C B A

Model with Residual Treatment n These designs are not orthogonal since each treatment cannot follow itself. We analyze using Type III SS (i indexes period, j indexes treatment)

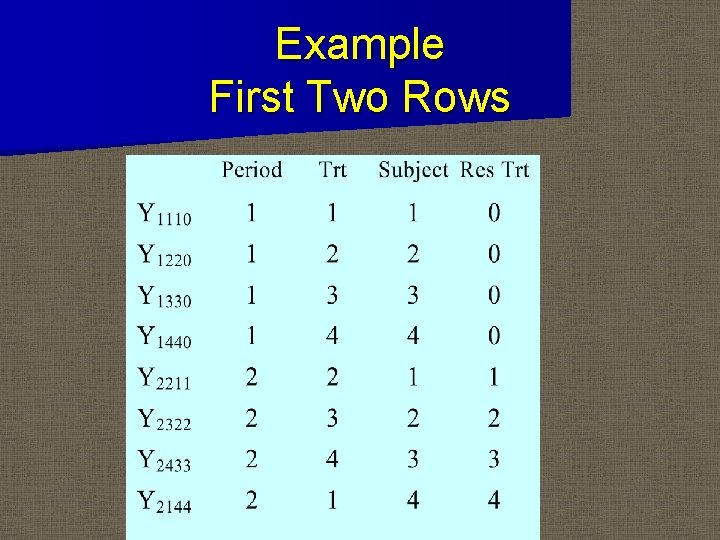
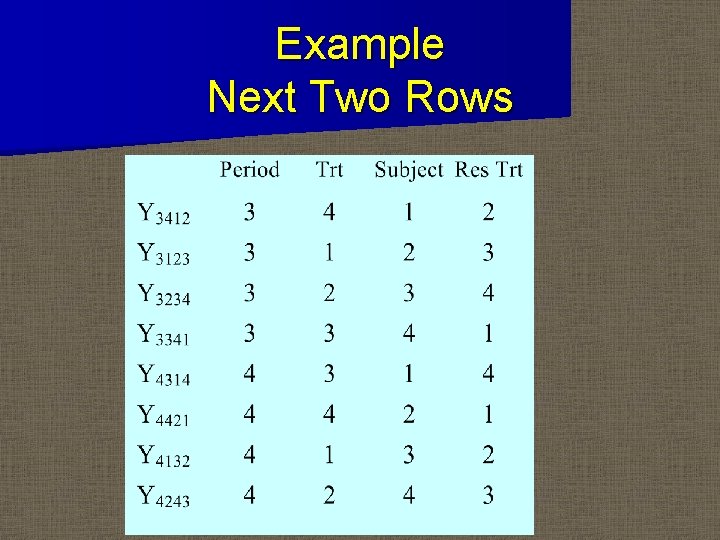
Residual Treatment Example n Example: A B D C B C A D C D B A D A C B

Example First Two Rows

Example Next Two Rows

Residual Treatment Effects n The parameter go is the effect of being in the first row--it is confounded with the period 1 effect and will not be estimated n Each of these factors loses a df as a result

Residua Treatment ANOVA Source Treatment Period Subject Res Trt Error Total Usual df Type III df n-1 n-1 n-2 sn-1 n n-1 By subtraction sn 2 -1