Repeated Measures ANOVA Prof Wei Zhu Department of

Repeated Measures ANOVA Prof. Wei Zhu Department of Applied Mathematics & Statistics Stony Brook University

Review of (the non-repeated measures) ANOVA 2

Review of ANOVA The One-way ANOVA we have just learnt can test the equality of several population means. It is an extension of the pooled variance t-test That is: H 0 (null hypothesis) : µ 1 = µ 2 = µ 3 =……. . = µk Ha (alternative hypothesis): At least one of means differs from the rest. Assumptions: Unknown but equal population variances Normal populations Independent samples 3

The F statistic where xij = the jth observation in the i th sample. 4

The ANOVA table Source S. S d. f, M. S. F Between Within The ANOVA table is a tool for displaying the computations for the F test. It is very important when the Between Sample variability is due to two or more factors. We reject the ANOVA null hypothesis of equal means if F > Fk-1, N-k, α 5

Limitations of the one-way ANOVA: The most distinct disadvantage to the analysis of variance (ANOVA) method is that it requires three assumptions to be made: ☼ The samples must be independent to each other. ☼ All variances from each data group, though unknown, must be equal. The normality assumption. 6

7

☼ A repeated measures design is one in which at least one of the factors consists of repeated measurements on the same subjects or experimental units, under different conditions and/or at different time points. 8

A repeated measures design often involves measuring subjects at different points in time – or subjects measured under different experimental conditions It can be viewed as an extension of the paired-samples t-test (which involved only two related measures) Thus, the measures—unlike in the “regular” ANOVA—are correlated, that is, the observations are not independent 9

Example: Data collected in a sequence of (often) evenly spaced points in time – this is usually referred to as the ‘longitudinal data’ Example: Different treatments are assigned to the each experimental unit 10

By collecting data from the same participants under repeated conditions, the individual differences can be eliminated or reduced as a source of between group differences. Also, the sample size is not divided between conditions or groups and thus inferential testing becomes more powerful. This design also proves to be economical when sample members are difficult to 11 recruit.

12

As with any ANOVA, repeated measures ANOVA tests the equality of means. However, repeated measures ANOVA is used when all members of a random sample are measured under a number of different conditions or at different time points. As the sample is exposed to each condition, the measurement of the dependent variable is repeated. Using a standard ANOVA in this case is not appropriate because it fails to model the correlation between the repeated measures: the data violate the ANOVA assumption of independence. 13

The simplest example of a repeated measures design is a paired samples t-test: Each subject is measured twice, for example, time 1 and time 2, on the same variable; or, each pair of matched participants are assigned to two treatment levels. If we observe participants at more than two time-points, then we need to conduct a repeated measures ANOVA. 14

What we would like to do is to decompose the variability into： (1) A random ‘subject’ effect (2) A fixed ‘treatment’ or ‘time’ effect Treating the subject as a random effect has the added advantage that we can extend our conclusion to the population where these subjects were drawn from. 15

Yij = μj +Si+εij μj = The fixed effect, j=1, ⋯, k Si= The random effect of subject i, i=1, ⋯, n εij = The random error independent of Si Furthermore, we set the total number of observations as: N = n*k 16

17 17

18

We will reject the ANOVA null hypothesis if Fk-1, (k-)(n-1) > α 19

20

Assumptions – summary: For a repeated measures design, we start with the same assumptions as a paired samples t-test : Participants are independent and randomly selected from the population Normality Then, very importantly, there are two approaches to repeated measures ANOVA depends on the assumption of the variance -covariance matrix: ☺ the univariate approach (where compound symmetry is imposed), and ☺ the multivariate approach (where no assumption is imposed) 21

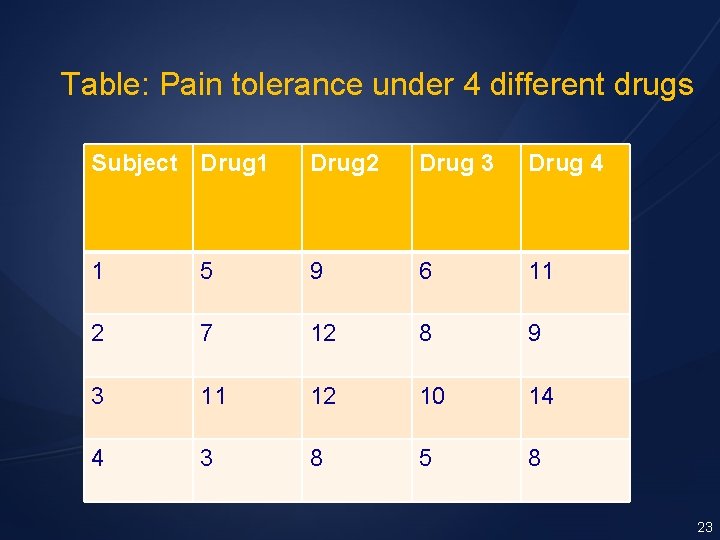
Example: Consider the following experiment: We have four drugs (1, 2, 3 and 4) that relieve pain. Each subject is given each of the four drugs. The subject’s pain tolerance is then measured. Enough time is allowed to pass between successive drug administrations so that we can be sure there is no residual effect from the previous drug. The null hypothesis is: Mean(1)=Mean(2)=Mean(3)=Mean(4) 22

Table: Pain tolerance under 4 different drugs Subject Drug 1 Drug 2 Drug 3 Drug 4 1 5 9 6 11 2 7 12 8 9 3 11 12 10 14 4 3 8 5 8 23

In the one-way analysis of variance without a repeated measure, we would have each subject receive only one of the four drugs. In this design, each subjects is measured under each of the drug conditions. This has several important advantages as enumerated before. 24

Each subject acts as his own control. i. e. : drugs effects are calculated by recording deviations between each drug score and the average drug score for each subject. The normal subject-to-subject variation can thus be removed from the error sum of squares. 25

26

27

SAS code using the REPEATED Statement DATA REPEAT; INPUT SUBJ PAIN 1 -PAIN 4; DATALINES; 1 5 9 6 11 2 7 12 8 9 3 11 12 10 14 43858 ; PROC ANOVA DATA=REPEAT; TITLE 'using repeated statement'; MODEL PAIN 1 -PAIN 4 = / NOUNI; REPEATED DRUG 4 (1 2 3 4) / printe; RUN; ☺ Please see Quiz 3 solutions for detailed explanations of the SAS 28

SAS code using the REPEATED Statement Remark 1 : about the data set We need the data set in the form: SUBJ PAIN 1 PAIN 2 PAIN 3 PAIN 4 NOTICE that it does not have a DRUG variable 29

SAS code using the REPEATED Statement Remark 2 : about the REPEATED Statement The general form: To compute pairwise comparisons REPEATED factor_name CONTRAST(n); • N is a number from 1 to k, with k being # levels of repeated factor; • To get all pairwise contrasts, we need k-1 repeated statements 30

SAS code using the REPEATED Statement Remark 2 : about the REPEATED Statement In our example: Request ANOVA tables for each contrast PROC ANOVA DATA=REPEAT; TITLE 'using repeated statement'; MODEL PAIN 1 -PAIN 4 = / NOUNI; REPEATED DRUG 4 CONTRAST(1) / SUMMARY; REPEATED DRUG 4 CONTRAST(2) / SUMMARY; REPEATED DRUG 4 CONTRAST(3) / SUMMARY; RUN; 31

SAS code using the REPEATED Statement Remark 3 : more explanation of the ANOVA procedure PROC ANOVA DATA=REPEAT; TITLE 'using repeated statement'; MODEL PAIN 1 -PAIN 4 = / NOUNI; REPEATED DRUG 4 (1 2 3 4) / printe; RUN; • No CLASS: our data set does not have an independent variable • NOUNI: not to conduct a separate analysis for each of the four PAIN • 4: the repeated factor “DRUG” has four levels; optional • (1 2 3 4): the labels we want printed for each level of DRUG • printe calls for the Machly’s Sphericity Test for compound symmetry 32

SAS code using the REPEATED Statement Remark 4 : Data conversion: the long form & the broad form DATA PAIN; INPUT SUBJ DRUG PAIN; DATALINES; 115 129 136 1 4 11 217 2 2 12 …… ; DATA PAIN; INPUT SUBJ @; DO DRUG = 1 to 4; INPUT PAIN @; OUTPUT; END; DATALINES; 1 5 9 6 11 2 7 12 8 9 3 11 12 10 14 43858 ; The following is the data format, the broad form, that You should master first. DATA REPEAT; INPUT SUBJ PAIN 1 -PAIN 4; DATALINES; 1 5 9 6 11 2 7 12 8 9 3 11 12 10 14 43858 ; 33

DATA PAIN; The long form! To keep reading from the same line of data INPUT SUBJ @; DO DRUG = 1 to 4; iterative loop INPUT PAIN @; OUTPUT; END; DATALINES; 1 5 9 6 11 2 7 12 8 9 The broad form! 3 11 12 10 14 43858 ; Generate data in long form from the broad form 34

SAS: The DO loop the general form: initial value ending value Do variable = start TO end BY increment; (SAS Statements) Default: 1 END; 35

SAS: The DO loop in our example: initial value: 1 ending value: 4 DO DRUG = 1 to 4; INPUT PAIN @; OUTPUT; to keep reading from the same line of d END; return to “DO” 36

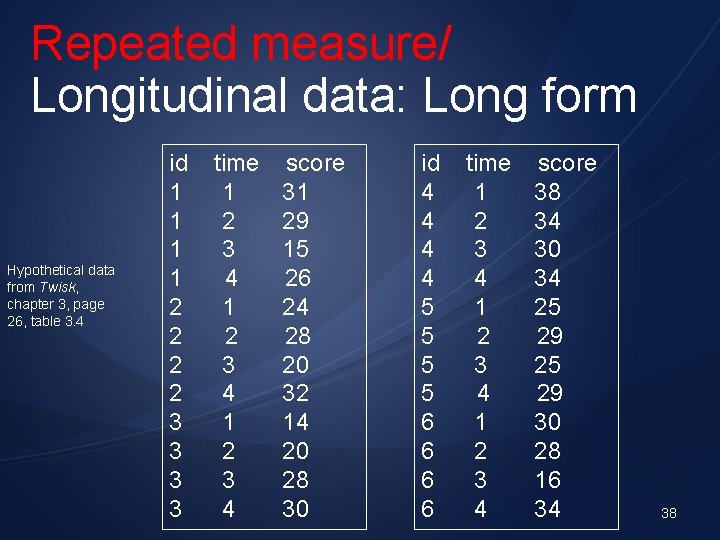
Repeated measure / Longitudinal data: broad form id 1 2 3 4 5 6 time 1 time 2 time 3 time 4 31 24 14 38 25 30 29 28 20 34 29 28 15 20 28 30 25 16 26 32 30 34 29 34 Hypothetical data from Twisk, chapter 3, page 26, table 3. 4 37 Jos W. R. Twisk. Applied Longitudinal Data Analysis for Epidemiology: A Practical Guide. Cambridge University Press, 2003.

Repeated measure/ Longitudinal data: Long form Hypothetical data from Twisk, chapter 3, page 26, table 3. 4 id 1 1 2 2 3 3 time 1 2 3 4 score 31 29 15 26 24 28 20 32 14 20 28 30 id 4 4 5 5 6 6 time 1 2 3 4 score 38 34 30 34 25 29 30 28 16 34 38

Another way to convert data from broad form to long form in SAS: data long; set broad; time=1; score=time 1; time=2; score=time 2; time=3; score=time 3; time=4; score=time 4; run; output; The long form is used to plot the profile plot in the same way as the usual ANOVA 39

40

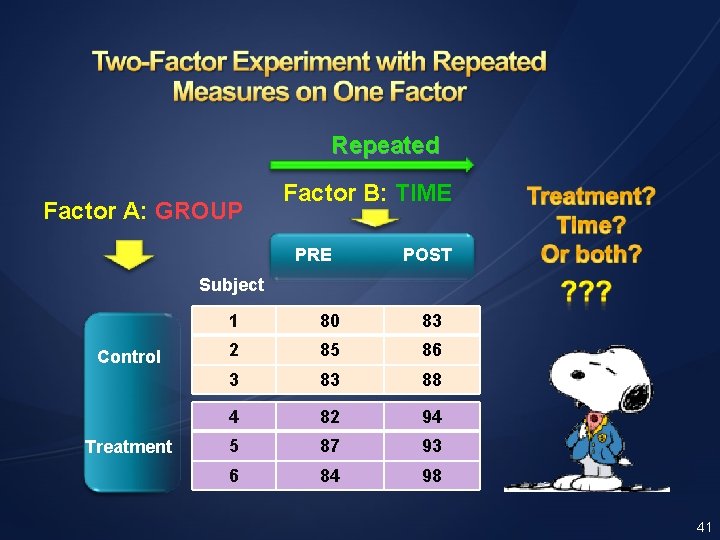
Repeated Factor A: GROUP Factor B: TIME PRE POST Subject Control Treatment 1 80 83 2 85 86 3 83 88 4 82 94 5 87 93 6 84 98 41

42

43

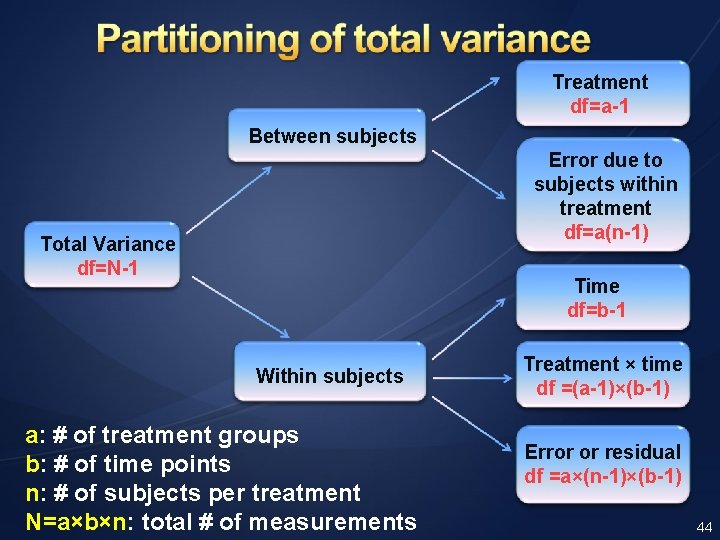
Treatment df=a-1 Between subjects Error due to subjects within treatment df=a(n-1) Total Variance df=N-1 Time df=b-1 Within subjects a: # of treatment groups b: # of time points n: # of subjects per treatment N=a×b×n: total # of measurements Treatment × time df =(a-1)×(b-1) Error or residual df =a×(n-1)×(b-1) 44

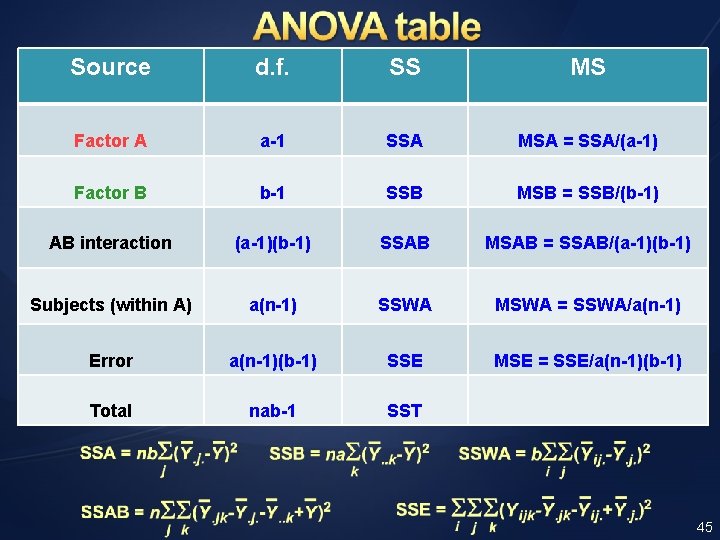
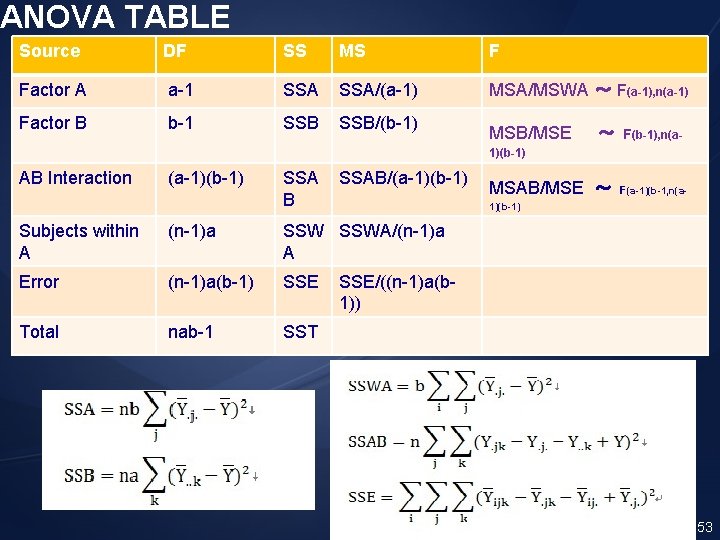
Source d. f. SS MS Factor A a-1 SSA MSA = SSA/(a-1) Factor B b-1 SSB MSB = SSB/(b-1) AB interaction (a-1)(b-1) SSAB MSAB = SSAB/(a-1)(b-1) Subjects (within A) a(n-1) SSWA MSWA = SSWA/a(n-1) Error a(n-1)(b-1) SSE MSE = SSE/a(n-1)(b-1) Total nab-1 SST 45

46

Data prepost; Input subj group $ pretest postest; datalines; 1 c 80 83 2 c 85 86 3 c 83 88 4 t 82 94 5 t 87 93 6 t 84 98 ; run; proc anova data=prepost; title 'Two-way ANOVA with a Repeated Measure on One Factor'; class group; model pretest postest = group/nouni; repeated time 2 (0 1); run; 47

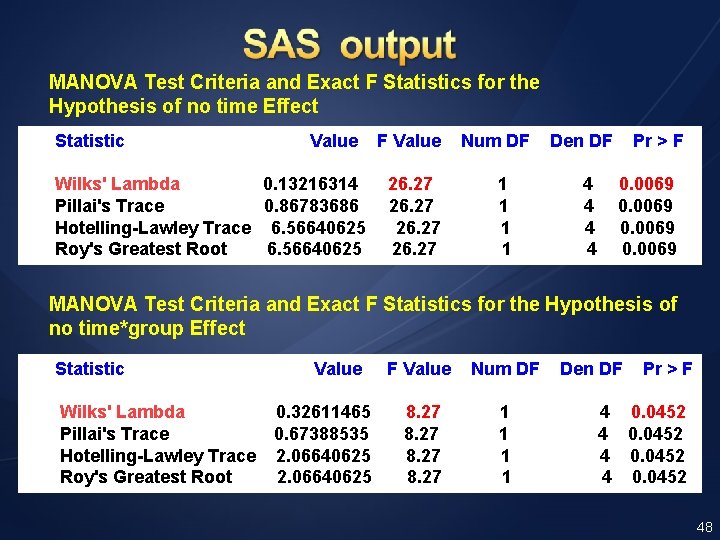
MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no time Effect Statistic Value F Value Num DF Den DF Pr > F Wilks' Lambda 0. 13216314 26. 27 1 4 0. 0069 Pillai's Trace 0. 86783686 26. 27 1 4 0. 0069 Hotelling-Lawley Trace 6. 56640625 26. 27 1 4 0. 0069 Roy's Greatest Root 6. 56640625 26. 27 1 4 0. 0069 MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no time*group Effect Statistic Value F Value Num DF Den DF Pr > F Wilks' Lambda 0. 32611465 8. 27 1 4 0. 0452 Pillai's Trace 0. 67388535 8. 27 1 4 0. 0452 Hotelling-Lawley Trace 2. 06640625 8. 27 1 4 0. 0452 Roy's Greatest Root 2. 06640625 8. 27 1 4 0. 0452 48

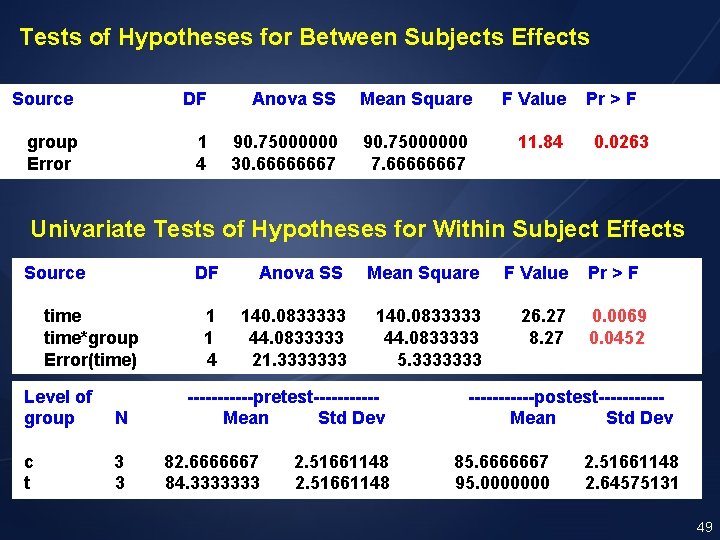
Tests of Hypotheses for Between Subjects Effects Source DF Anova SS Mean Square F Value Pr > F group 1 90. 75000000 11. 84 0. 0263 Error 4 30. 66666667 7. 66666667 Univariate Tests of Hypotheses for Within Subject Effects Source DF Anova SS Mean Square F Value Pr > F time 1 140. 0833333 26. 27 0. 0069 time*group 1 44. 0833333 8. 27 0. 0452 Error(time) 4 21. 3333333 5. 3333333 Level of ------pretest------ ------postest----- group N Mean Std Dev c 3 82. 6666667 2. 51661148 85. 6666667 2. 51661148 t 3 84. 3333333 2. 51661148 95. 0000000 2. 64575131 49

Another Example 50

Two-Factor ANOVA with Repeated Measures on One Factor 51

Hypothesis 52

ANOVA TABLE Source DF SS MS F Factor A a-1 SSA/(a-1) MSA/MSWA ～ F(a-1), n(a-1) Factor B b-1 SSB/(b-1) MSB/MSE ～ F(b-1), n(a- 1)(b-1) AB Interaction (a-1)(b-1) SSA B SSAB/(a-1)(b-1) MSAB/MSE ～ F(a-1)(b-1, n(a 1)(b-1) Subjects within A (n-1)a SSWA/(n-1)a A Error (n-1)a(b-1) SSE Total nab-1 SST SSE/((n-1)a(b 1)) 53

Example Six subjects, equally divided between two calibration method groups (calib), and each with 4 accuracy scores measured over 4 different dial shapes (repeated measures). 54

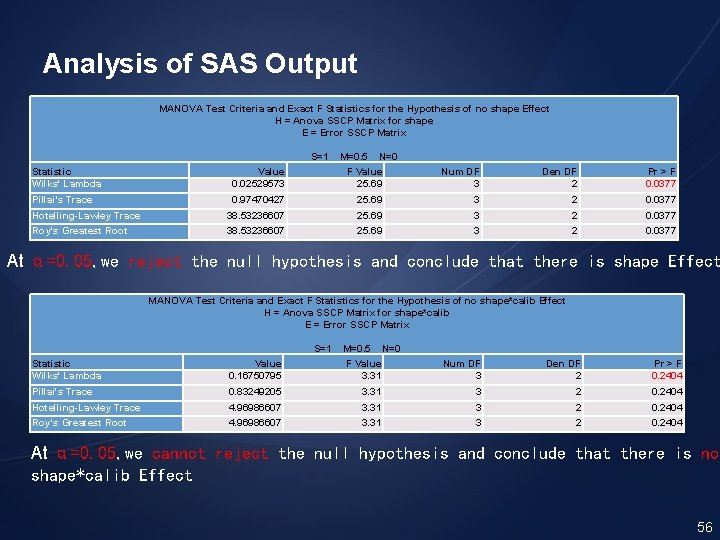
Data dials; Input subj calib shape_1 shape_2 shape_3 shape_4; datalines; 1 1 0 0 5 3 2 1 3 1 5 4 3 1 4 3 6 2 4 2 7 8 5 2 5 4 6 6 6 2 7 5 8 9 ; run; proc anova data=dials; title 'Two-way ANOVA with a Repeated Measure on One Factor'; class calib; model shape_1 shape_2 shape_3 shape_4 = calib/nouni; repeated shape 4; run; 55

Analysis of SAS Output MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no shape Effect H = Anova SSCP Matrix for shape E = Error SSCP Matrix S=1 M=0. 5 N=0 Statistic Wilks' Lambda Value 0. 02529573 F Value 25. 69 Num DF 3 Den DF 2 Pr > F 0. 0377 Pillai's Trace 0. 97470427 25. 69 3 2 0. 0377 Hotelling-Lawley Trace 38. 53236607 25. 69 3 2 0. 0377 Roy's Greatest Root 38. 53236607 25. 69 3 2 0. 0377 At α=0. 05, we reject the null hypothesis and conclude that there is shape Effect MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no shape*calib Effect H = Anova SSCP Matrix for shape*calib E = Error SSCP Matrix S=1 M=0. 5 N=0 Statistic Wilks' Lambda Value 0. 16750795 F Value 3. 31 Num DF 3 Den DF 2 Pr > F 0. 2404 Pillai's Trace 0. 83249205 3. 31 3 2 0. 2404 Hotelling-Lawley Trace 4. 96986607 3. 31 3 2 0. 2404 Roy's Greatest Root 4. 96986607 3. 31 3 2 0. 2404 At α=0. 05, we cannot reject the null hypothesis and conclude that there is no shape*calib Effect 56

Tests of Hypotheses for Between Subjects Effects Source calib Error DF 1 Anova SS 51. 04166667 Mean Square 51. 04166667 4 17. 16666667 4. 29166667 F Value 11. 89 Pr > F 0. 0261 At α=0. 05, we reject the null hypothesis and conclude there is calibration Effect Univariate Tests of Hypotheses for Within Subject Effects Adj Pr > F Source shape DF 3 Anova SS 47. 45833333 Mean Square 15. 81944444 F Value 12. 80 Pr > F 0. 0005 G - G 0. 0099 H - F 0. 0011 shape*calib 3 7. 45833333 2. 48611111 2. 01 0. 1662 0. 2152 0. 1791 Error(shape) 12 14. 83333333 1. 23611111 Greenhouse-Geisser Epsilon 0. 4751 Huynh-Feldt Epsilon 0. 8483 Since the G-G epsilon is rather small, we choose to use the conservative G-G correction. 57

58

Two-Factor ANOVA with Repeated Measures on both Factors 59

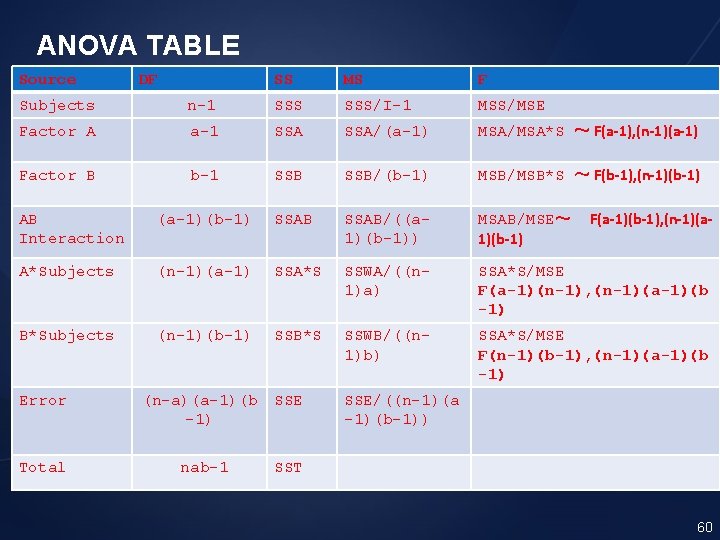
ANOVA TABLE Source DF SS MS F Subjects n-1 SSS/I-1 MSS/MSE Factor A a-1 SSA/(a-1) MSA/MSA*S ～ F(a-1), (n-1)(a-1) Factor B b-1 SSB/(b-1) MSB/MSB*S ～ F(b-1), (n-1)(b-1) F(a-1)(b-1), (n-1)(a- AB Interaction (a-1)(b-1) SSAB/((a 1)(b-1)) MSAB/MSE～ 1)(b-1) A*Subjects (n-1)(a-1) SSA*S SSWA/((n 1)a) SSA*S/MSE F(a-1)(n-1), (n-1)(a-1)(b -1) B*Subjects (n-1)(b-1) SSB*S SSWB/((n 1)b) SSA*S/MSE F(n-1)(b-1), (n-1)(a-1)(b -1) SSE/((n-1)(a -1)(b-1)) Error Total (n-a)(a-1)(b -1) nab-1 SST 60

Example Three subjects, each with nine accuracy scores on all combinations of the three different dials and three different periods. Here subject is a random factor and both dial and period are fixed factors. 61

SAS Code Data Q 2; Input subj Mins 1 -Mins 9; Datalines; 1 45 53 60 40 52 57 28 37 46 2 35 41 50 30 37 47 28 32 41 3 60 65 75 58 54 70 40 47 50 ; ODS RTF STYLE=Barretts. Blue; Proc anova data=Q 2; Model Mins 1 -Mins 9=/nouni; Repeated period 3, dial 3/nom; Run; ods rtf close; 62

Since all epsilons < 0. 75, we Should use the G-G correction. SAS Output Univariate Tests of Hypotheses for Within Subject Effects Source period Error(period) DF 2 4 Anova SS 1072. 666667 148. 444444 Adj Pr > F H - F Mean Square F Value Pr > F G - G 536. 333333 14. 45 0. 0148 0. 0563 0. 0394 37. 111111 Greenhouse-Geisser Epsilon 0. 5364 Huynh-Feldt Epsilon 0. 6569 At α=0. 05, we can not reject the null hypothesis and conclude that the period Effect is marginal. Source dial Error(dail) DF 2 4 Anova SS 978. 6666667 38. 4444444 Mean Square 489. 3333333 9. 6111111 F Value Pr > F 50. 91 0. 0014 Adj Pr > F G - G H - F 0. 0169 0. 0115 Greenhouse-Geisser Epsilon 0. 5227 Huynh-Feldt Epsilon 0. 5952 At α=0. 05, we reject the null hypothesis and conclude that there is dial Effect Adj Pr > F Source period*dial Error(period*dial) DF 4 Anova SS Mean Square F Value Pr > F G - G H - F 8. 66666667 2. 16666667 0. 30 0. 8715 0. 6603 0. 7194 8 58. 2222 Greenhouse-Geisser Epsilon 0. 2827 Huynh-Feldt Epsilon 0. 4006 7. 27777778 At α=0. 05, we cannot reject the null hypothesis and conclude there is no period*dail Effect 63

Another Example 64

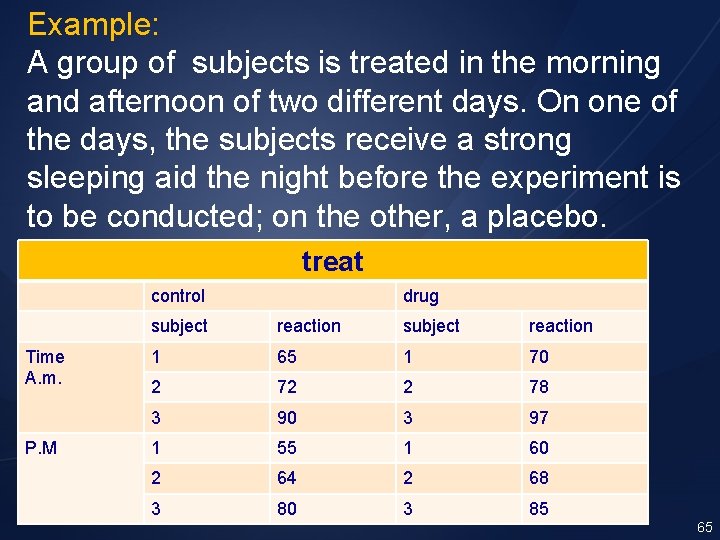
Example: A group of subjects is treated in the morning and afternoon of two different days. On one of the days, the subjects receive a strong sleeping aid the night before the experiment is to be conducted; on the other, a placebo. treat control Time A. m. P. M drug subject reaction 1 65 1 70 2 72 2 78 3 90 3 97 1 55 1 60 2 64 2 68 3 80 3 85 65

SAS Code data repeat; input subj react 1 -react 4; datalines; 1 65 70 55 60 proc anova data=repeat; 2 72 78 64 68 model react 1 -react 4= /nouni; 3 90 97 80 85 repeated time 2, treat 2; ; run; 66

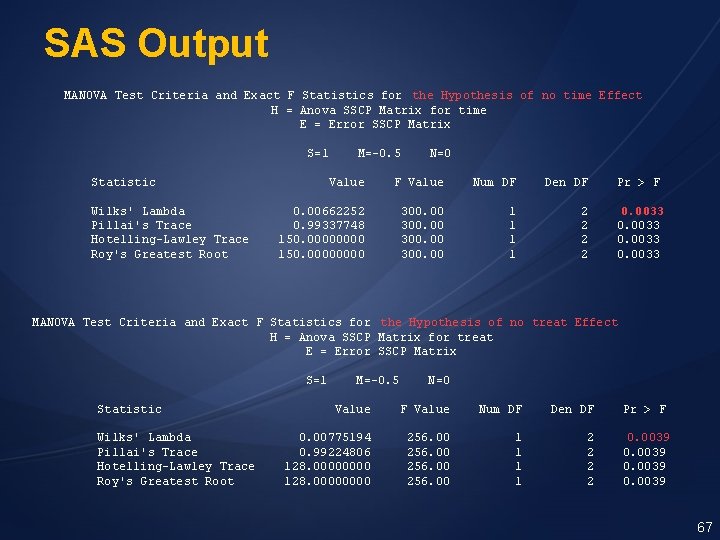
SAS Output MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no time Effect H = Anova SSCP Matrix for time E = Error SSCP Matrix S=1 Statistic Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root M=-0. 5 N=0 Value F Value Num DF Den DF 0. 00662252 0. 99337748 150. 00000000 300. 00 1 1 2 2 Pr > F 0. 0033 MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no treat Effect H = Anova SSCP Matrix for treat E = Error SSCP Matrix S=1 Statistic Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root M=-0. 5 N=0 Value F Value Num DF Den DF 0. 00775194 0. 99224806 128. 00000000 256. 00 1 1 2 2 Pr > F 0. 0039 67

MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no time*treat Effect H = Anova SSCP Matrix for time*treat E = Error SSCP Matrix S=1 Statistic Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root M=-0. 5 N=0 Value F Value Num DF Den DF 0. 3333 0. 66666667 2. 00000000 4. 00 1 1 2 2 Pr > F 0. 1835 Thus we conclude that there are significant main effects, but their interaction is not significant.

Interpretation According to the observed p-values, except for the interactions, we can reject the hypotheses that time and treat are not significantly different. The drug increase reaction time Reaction time is longer in the morning compared to the afternoon The interaction of treat and time is not 69

70

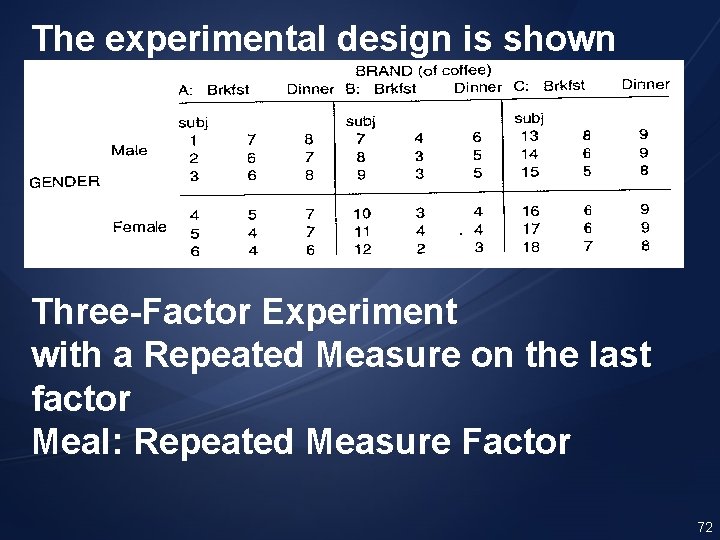
Consider a marketing experiment: Male and female subjects are offered one of three different brands of coffee. Each brand is tasted twice; once after breakfast, the other time after dinner. The preference of each brand is measured on a scale from 1 to 10 (1=lowest, 10=highest). 71

The experimental design is shown below: Three-Factor Experiment with a Repeated Measure on the last factor Meal: Repeated Measure Factor 72

SAS Program: 73

OUTPUT(Part 1/4): 74

OUTPUT(Part 2/4): 75

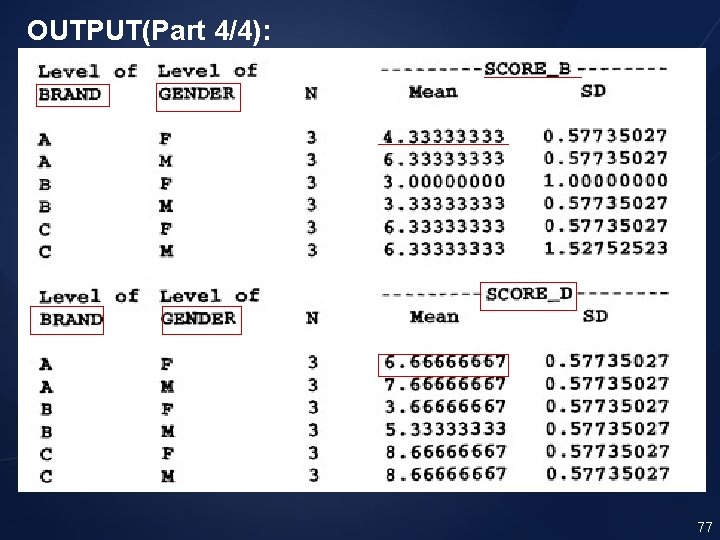
OUTPUT(Part 3/4): 76

OUTPUT(Part 4/4): 77

78

79

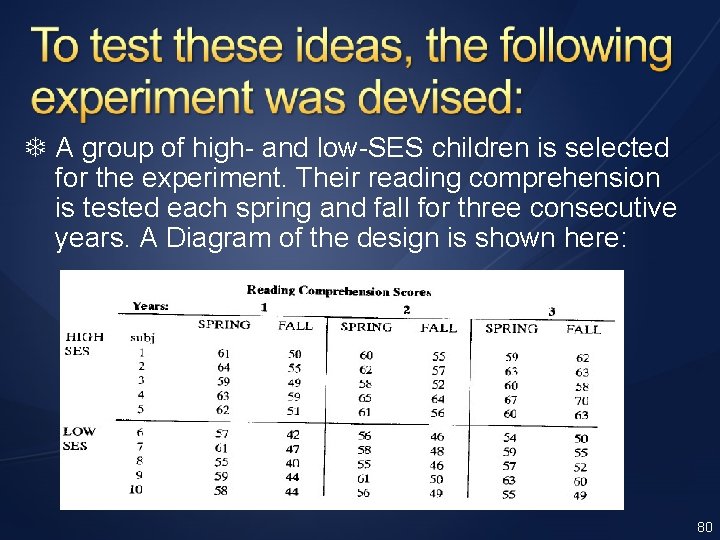
A group of high- and low-SES children is selected for the experiment. Their reading comprehension is tested each spring and fall for three consecutive years. A Diagram of the design is shown here: 80

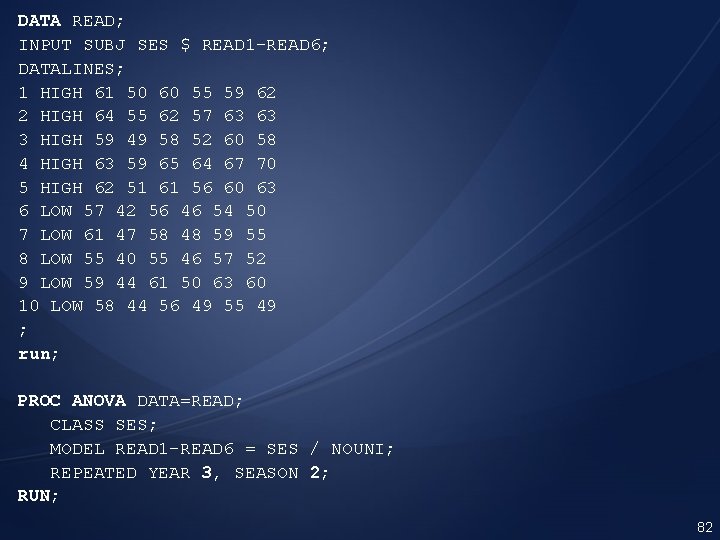
Notice that each subject is measured every spring and fall of each year so that the variables SEASON and YEAR are both repeated measures factors. 81

DATA READ; INPUT SUBJ SES $ READ 1 -READ 6; DATALINES; 1 HIGH 61 50 60 55 59 62 2 HIGH 64 55 62 57 63 63 3 HIGH 59 49 58 52 60 58 4 HIGH 63 59 65 64 67 70 5 HIGH 62 51 61 56 60 63 6 LOW 57 42 56 46 54 50 7 LOW 61 47 58 48 59 55 8 LOW 55 40 55 46 57 52 9 LOW 59 44 61 50 63 60 10 LOW 58 44 56 49 55 49 ; run; PROC ANOVA DATA=READ; CLASS SES; MODEL READ 1 -READ 6 = SES / NOUNI; REPEATED YEAR 3, SEASON 2; RUN; 82

☺ Since the REPEATED statement is confusing when we have more than one repeated factor, it is important for you to know how to determine the order of the factor names. Look at the REPEATED statement in this example: REPEATED YEAR 3, SEASON 2; This statement instructs the ANOVA procedure to choose the first level of YEAR(1), then loop through two levels of SEASON(SPRING FALL), then return to the next level of YEAR(2), followed by two levels of SEASON, etc. 83

SAS Output MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no YEAR Effect H = Anova SSCP Matrix for YEAR E = Error SSCP Matrix S=1 Statistic M=0 Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root N=2. 5 Value F Value Num DF Den DF 0. 19558215 0. 80441785 4. 11294094 14. 40 2 2 7 7 Pr > F 0. 0033 MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no YEAR*SES Effect H = Anova SSCP Matrix for YEAR*SES E = Error SSCP Matrix S=1 Statistic Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root M=0 N=2. 5 Value F Value Num DF Den DF 0. 96176044 0. 03823956 0. 03975996 0. 14 2 2 7 7 Pr > F 0. 8724 84

MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no SEASON Effect H = Anova SSCP Matrix for SEASON E = Error SSCP Matrix S=1 Statistic M=-0. 5 Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root N=3 Value F Value Num DF Den DF 0. 03436198 0. 96563802 28. 10192837 224. 82 1 1 8 8 Pr > F <. 0001 MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no SEASON*SES Effect H = Anova SSCP Matrix for SEASON*SES E = Error SSCP Matrix S=1 Statistic Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root M=-0. 5 N=3 Value F Value Num DF Den DF 0. 17759295 0. 82240705 4. 63085399 37. 05 1 1 8 8 Pr > F 0. 0003

MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no YEAR*SEASON Effect H = Anova SSCP Matrix for YEAR*SEASON E = Error SSCP Matrix S=1 Statistic M=0 Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root N=2. 5 Value F Value Num DF Den DF 0. 03714436 0. 96285564 25. 92198764 90. 73 2 2 7 7 Pr > F <. 0001 MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no YEAR*SEASON*SES Effect H = Anova SSCP Matrix for YEAR*SEASON*SES E = Error SSCP Matrix S=1 Statistic Wilks' Lambda Pillai's Trace Hotelling-Lawley Trace Roy's Greatest Root M=0 N=2. 5 Value F Value Num DF Den DF 0. 91603774 0. 08396226 0. 09165808 0. 32 2 2 7 7 Pr > F 0. 7357

The ANOVA Procedure Repeated Measures Analysis of Variance Tests of Hypotheses for Between Subjects Effects Source SES Error DF Anova SS Mean Square F Value 1 8 680. 0666667 401. 6666667 680. 0666667 50. 2083333 13. 54 Pr > F 0. 0062

In this case, one can use either the G-G or the H-F corrections. The ANOVA Procedure Repeated Measures Analysis of Variance Univariate Tests of Hypotheses for Within Subject Effects Source DF Anova SS Mean Square F Value Pr > F YEAR*SES Error(YEAR) 2 2 16 252. 0333333 1. 0333333 74. 9333333 126. 0166667 0. 5166667 4. 6833333 26. 91 0. 11 <. 0001 0. 8962 Greenhouse-Geisser Epsilon Huynh-Feldt Epsilon Source SEASON*SES Error(SEASON) Adj Pr > F G - G H - F 0. 0002 0. 8186 0. 6757 0. 8658 DF Anova SS Mean Square F Value Pr > F 1 1 8 680. 0666667 112. 0666667 24. 2000000 680. 0666667 112. 0666667 3. 0250000 224. 82 37. 05 <. 0001 0. 0003 Source DF Anova SS Mean Square F Value Pr > F YEAR*SEASON*SES Error(YEAR*SEASON) 2 2 16 265. 4333333 0. 4333333 18. 8000000 132. 7166667 0. 2166667 1. 1750000 112. 95 0. 18 <. 0001 0. 8333 Greenhouse-Geisser Epsilon Huynh-Feldt Epsilon <. 0001 0. 8700 0. 7073 0. 9221 Adj Pr > F G - G H - F <. 0001 0. 7592 <. 0001 0. 8168

Alternative SAS Procedures for Repeated Measures ANOVA We can use other SAS procedures such as: “Proc GLM” “Proc Mixed” 89

Acknowledgement My thanks go to: My students! Cody & Smith & their little SAS book where several examples were selected from. 90