REPASO 6 5 Propiedades del tensor de Inercia

REPASO 6. 5 Propiedades del tensor de Inercia Teorema de Steiner Q El segundo termino del lado de la derecha es el tensor de inercia de una masa puntual M referido al origen Q. Teorema de Steiner para momentos de inercia. a 2

6. 6 Ecuaciones Cardinales para un cuerpo rígido. Recordemos las ecuaciones cardinales para un sistema de partículas 1 era Cardinal: 2 da Cardinal: La primera cardinal para el cuerpo rígido no cambia.

Observación 1:

Sustituyendo en la ecuación obtenemos Que es válida cuando el movimiento es en un plano perpendicular al eje z.

6. 7 Sistemas de fuerzas aplicadas. 6. 7. 1

Antes de continuar, nos será útil introducir para el caso general de un sistema de partículas (no necesariamente un rígido) como se relacionan los torques de las fuerzas externas calculados Respecto a dos puntos diferentes de Q 1 a Q 2. Ejercicio: Probar que para el caso general de un sistema de partículas (no necesariamente un rígido, si cambiamos el punto en que calculamos el torque de Q 1 a Q 2, los torques de las fuerzas externas estarán relacionados así: ‘Formula de cambio de aplicación de torques o momentos de las fuerzas externas’

Par 6. 7. 2

6. 8 Estática de cuerpos rígidos. La situación de reposo de un cuerpo rígido corresponde a : Este estado se mantendrá si Demostraremos que: Para demostrar esto, comencemos recordando las ecuaciones cardinales para el cuerpo rígido: 1 era Cardinal: 2 da Cardinal: , de modo que es inmediato que La segunda cardinal si tomamos Q coincidiendo con el baricentro G se reduce a:

De modo que si Y es inmediato que se mantendrá si =0 Vimos que la formula de cambio del punto en que calculamos el torque de Q 1 a Q 2, nos dice que los torques de las fuerzas externas estarán relacionados así: Si tomamos Q 1 Q y Q 2 G, tendremos que: G =0 =0 Resultando entonces que

En el eje vertical tenemos: En el eje horizontal tenemos:

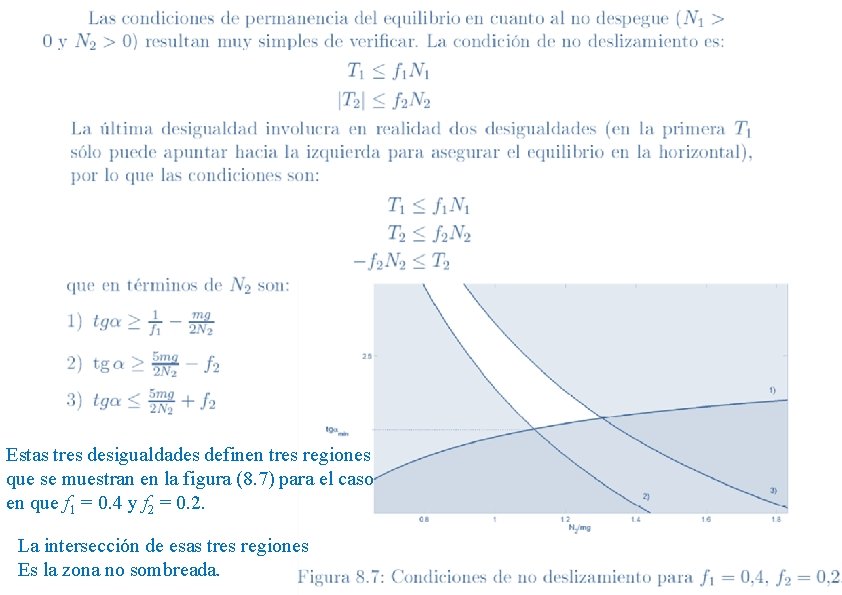
Estas tres desigualdades definen tres regiones que se muestran en la figura (8. 7) para el caso en que f 1 = 0. 4 y f 2 = 0. 2. La intersección de esas tres regiones Es la zona no sombreada.