Rep Invariant and Abstraction Function CS 247 Module

Rep. Invariant and Abstraction Function CS 247 Module 8 Scott Chen

Assigned Readings Ø Barbara Liskov and John Guttag, Program Development in Java: Abstraction, Specification, and Object Oriented Design • Chapter 5. 5 – Aids to Understanding Implementation • Read as needed to support the lecture contents • This lecture benefits from slides by Michael Ernst (Uwash) and Daniel Jackson (MIT)

Agenda for Module 8 Ø Definition of Abstract Data Representation Ø Representation Invariant (RI) • Examples of Rep. Invariant of an ADT • Ensuring Rep. Invariant is Always at Check Ø Abstraction Function (AF) • Idioms for Expressing AF • AF mapping between concrete and abstract operations

Section 1 Definition

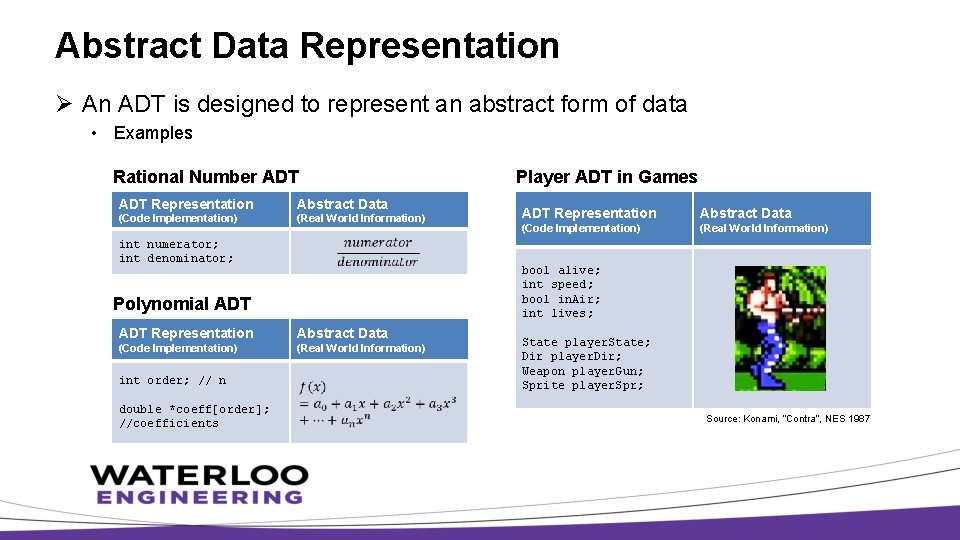
Abstract Data Representation Ø An ADT is designed to represent an abstract form of data • Examples Rational Number ADT Representation Abstract Data (Code Implementation) (Real World Information) int numerator; int denominator; ADT Representation Abstract Data (Code Implementation) (Real World Information) double *coeff[order]; //coefficients ADT Representation Abstract Data (Code Implementation) (Real World Information) bool alive; int speed; bool in. Air; int lives; Polynomial ADT int order; // n Player ADT in Games State player. State; Dir player. Dir; Weapon player. Gun; Sprite player. Spr; Source: Konami, “Contra”, NES 1987

Abstract Data Representation Ø Programmers are limited in using the data types the OOD languages have to offer to “reenact” a real-life object in the computer world Ø Abstract Data • The tangible object / concept in real-life, easily understood by human Ø Data Representation • • The OOD code implementation (data members) that closely models the tangible object / concept in real-life Allowing computers to run the program to reenact the abstract object / concept for clients Ø Abstraction Function • • A mathematical approach to modeling how abstract data is represented by the data representation NOT ALWAYS a math function. Mostly a concept.

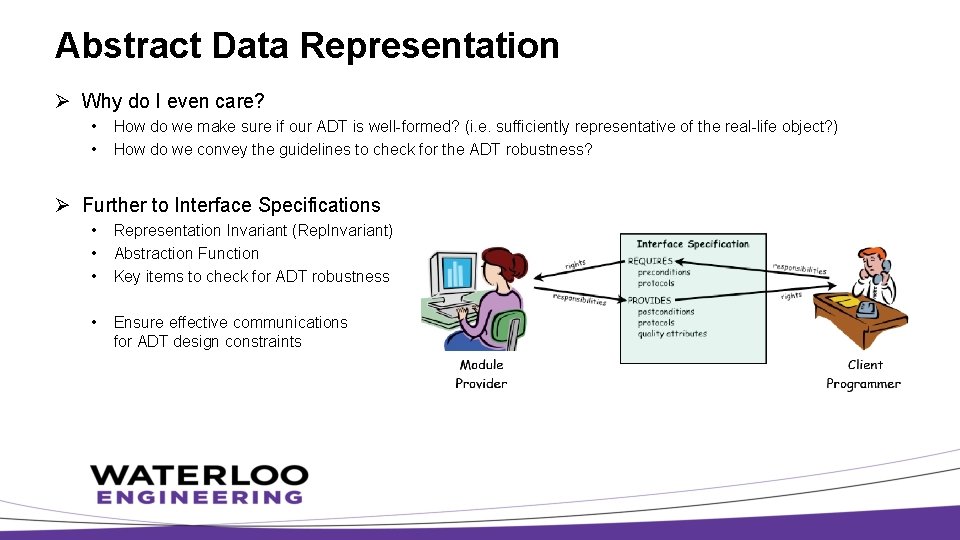
Abstract Data Representation Ø Why do I even care? • • How do we make sure if our ADT is well-formed? (i. e. sufficiently representative of the real-life object? ) How do we convey the guidelines to check for the ADT robustness? Ø Further to Interface Specifications • • • Representation Invariant (Rep. Invariant) Abstraction Function Key items to check for ADT robustness • Ensure effective communications for ADT design constraints

Section 2 Representation Invariant

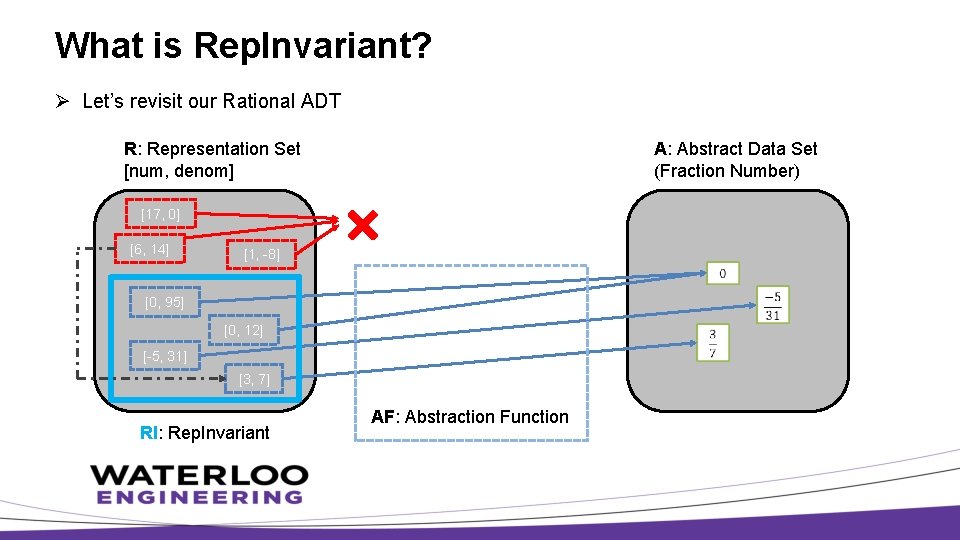
What is Rep. Invariant? Ø Let’s revisit our Rational ADT R: Representation Set [num, denom] A: Abstract Data Set (Fraction Number) [17, 0] [6, 14] [1, -8] [0, 95] [0, 12] [-5, 31] [3, 7] RI: Rep. Invariant AF: Abstraction Function

Rep. Invariant Ø

Rep. Invariant Ø Example – What is the RI of our Rational ADT? • Denominator must be positive and non-zero • Fraction must be in the most reduced form Ø An ADT is said to be well-formed when its RI is guaranteed at all times Ø Is our Rational ADT currently well-formed?

Rep. Invariant – Another Example Ø Consider the following Account ADT that tracks • • The account balance The history of all the transactions on the account class Account { int balance_; //Account Balance vector<Trans> transaction. History_; } class Trans { int amount_; public: int amount(){ return amount_; } … } • Implementation Constraints (Valid Values in R) • • RI for Account ADT • • What would be the RI of Account ADT? transaction. History_ != null The union of constraints in A and R

Rep. Invariant – Many More Examples Ø Structural invariants of the data structure chosen (e. g. Tree Structure) • Threes cannot have cycles § n 1. (left + right)* != n 1 • Two tree nodes cannot share the same descendent node § n 1 != n 2 => n 1. (left + right)* Ո n 2. (left + right)* == 0 • If implemented with doubly-linked list § n 1. next. prev == n 1 Ø Value invariants induced by data structure / algorithm chosen (e. g. Sorted Tree Structure) • No duplicate data elements § for all n 1, n 2: (n 1 != n 2 => n 1. data != n 2. data) • For all nodes n 1 in the tree that have a left subtree: § n 1. left. data < n 1. data

Rep. Invariant – Many More Examples Ø

Rep. Invariant – Robustness Check Ø Generally, an invariant is a property that is true for the entire program Ø An invariant of an object – a property true for the entire lifetime of the object Ø Thus, by structural induction, an ADT (or the RI thereof) is well-formed if 1. RI is established by constructor 2. RI is preserved by mutators 3. No representation exposure occurs

Rep. Invariant – Robustness Check Ø What can cause Representation Exposure? • Non-private data members (bad design practice to begin with…) • Client gains access to object inside the representation through a different path § e. g. external object accessible via external reference is incorporated into the ADT representation through some operations § Recall: Mutable objects present problems (module 3) • Operation outputs an object that is part of the representation § e. g. accessor outputs the reference to the internal collection / iterator that points to members of the internal collection

Rep. Invariant – Robustness Check Ø BDP: Rule of Thumb - Check Rep. Invariant… • • On exit of constructor On entry and on exit of accessors and mutators • Example: Remove an element from a Data Set void remove (Data* d) { This is where assert() is highly effective void check. Rep() { check. Rep(); // First, the set should have no duplicate values for(int i = 0; i < size_; i++) { assert( find. Index( elements_[i] ) == i ); } for(int i = 0; i < size_; i++) { if( elements_[i] == d ) { elements_[i] = elements_[size_ - 1]; size--; break; } } // Next, NULL values should be set for unused // slots in the set for(int i = size_; i < SET_MAX_SIZE; i++) { assert( elements_[i] == NULL ); } check. Rep(); } }

Rep. Invariant – Part of Specification Ø BDP: Documenting Rep. Invariants in ADT interface specification to help collaborators keep the robustness of RI in check Ø Example: Rational ADT class Rational { // Rep Invariant: // denominator_ > 0 // numerator_/denominator_ is in reduced form // // Safety from Rep Exposure // All fields are deployed in Pimpl // (should consider immutable implementation) public: … private: … };

Section 3 Abstraction Function

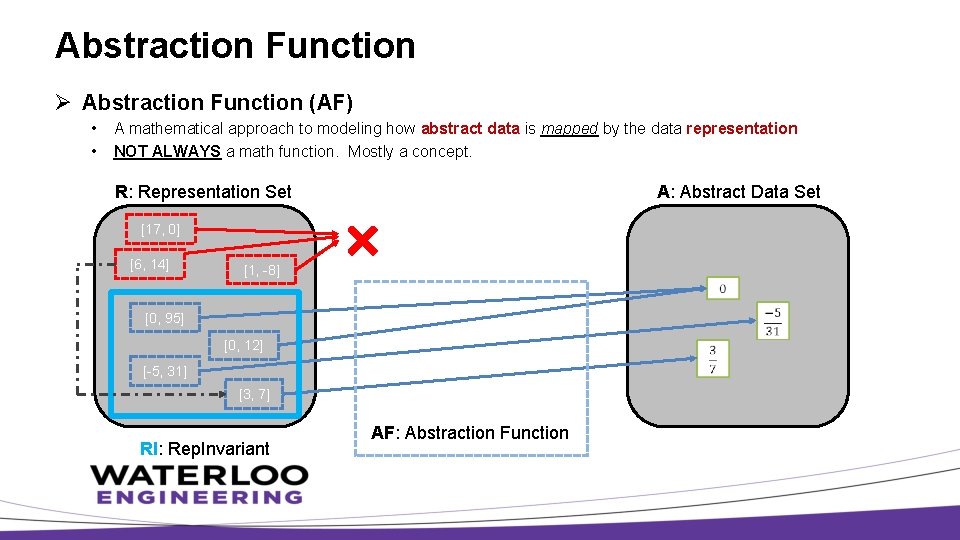
Abstraction Function Ø Abstraction Function (AF) • • A mathematical approach to modeling how abstract data is mapped by the data representation NOT ALWAYS a math function. Mostly a concept. R: Representation Set A: Abstract Data Set [17, 0] [6, 14] [1, -8] [0, 95] [0, 12] [-5, 31] [3, 7] RI: Rep. Invariant AF: Abstraction Function

Abstraction Function – Part of Specification Ø BDP: Documenting Abstraction Function in ADT interface specification to help collaborators keep the AF behaviour in check Ø Example: Rational ADT class Rational { // Rep Invariant: // denominator_ > 0 // numerator_/denominator_ is in reduced form // // Safety from Rep Exposure // All fields are deployed in Pimpl // (should consider immutable implementation) public: … private: … }; // Abstraction Function: represents thedenominator_) rational number // AF(numerator_, = numerator_ / denominator_ // numerator_ / denominator_

Abstraction Function – Expression Idioms Ø

AF: Concrete-Abstract Operation Mapping Ø Definition • Concrete Operation § An operation that modifies the data representation • Abstract Operation § An operation that modifies the real-life object Ø Concrete-Abstract Operation Mapping • “Not every concrete operation corresponds to a matching abstract operation” • BDP: Document-worthy in specifications to keep the AF behaviour in check

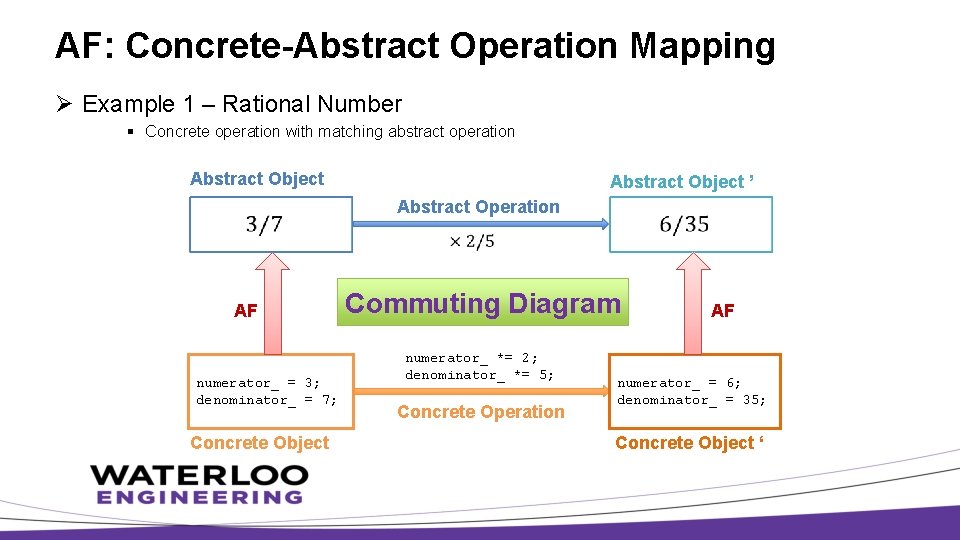
AF: Concrete-Abstract Operation Mapping Ø Example 1 – Rational Number § Concrete operation with matching abstract operation Abstract Object ’ Abstract Operation AF numerator_ = 3; denominator_ = 7; Concrete Object Commuting Diagram numerator_ *= 2; denominator_ *= 5; Concrete Operation AF numerator_ = 6; denominator_ = 35; Concrete Object ‘

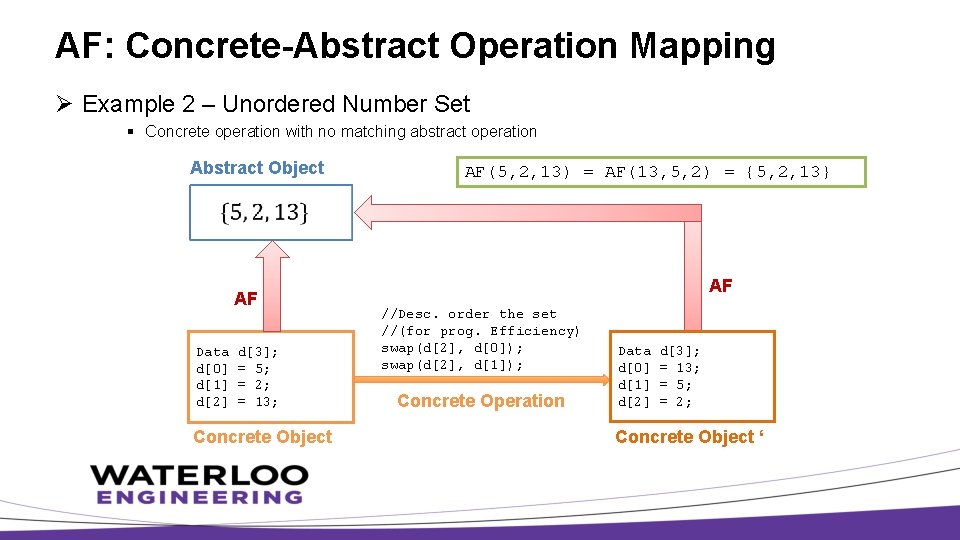
AF: Concrete-Abstract Operation Mapping Ø Example 2 – Unordered Number Set § Concrete operation with no matching abstract operation Abstract Object AF Data d[0] d[1] d[2] d[3]; = 5; = 2; = 13; Concrete Object AF(5, 2, 13) = AF(13, 5, 2) = {5, 2, 13} AF //Desc. order the set //(for prog. Efficiency) swap(d[2], d[0]); swap(d[2], d[1]); Concrete Operation Data d[0] d[1] d[2] d[3]; = 13; = 5; = 2; Concrete Object ‘

AF: Concrete-Abstract Operation Mapping Ø AF: Concrete-Abstract Operation Mapping “Not every concrete operation corresponds to a matching abstract operation” Ø Where else can we find this characteristics? • Project Phase 1 – Card Game • If you have a 5 -card flush in hand, swapping the order of the card does not alter this fact • Abstract Object § Flush • Representation R § 5 cards of consecutive numerical order, but does not necessarily have to be ordered.

Starting Point for Project 1

Summary

Summary Ø Abstract Data Representation • • • Abstract Object Data Representation Abstraction Function Ø Representation Invariant • • • Keep the ADT well-formed throughout the development Use in conjunction with assert() – pros and cons? Places to Guard § Constructor § Mutator § Places where Representation Exposure is likely Ø Abstraction Function • • Motivation and use of AF Concrete-Abstract operation mapping