Rendezsek Egyszer csers rendezs Algoritmus Elemcsere Egyszer csers

Rendezések

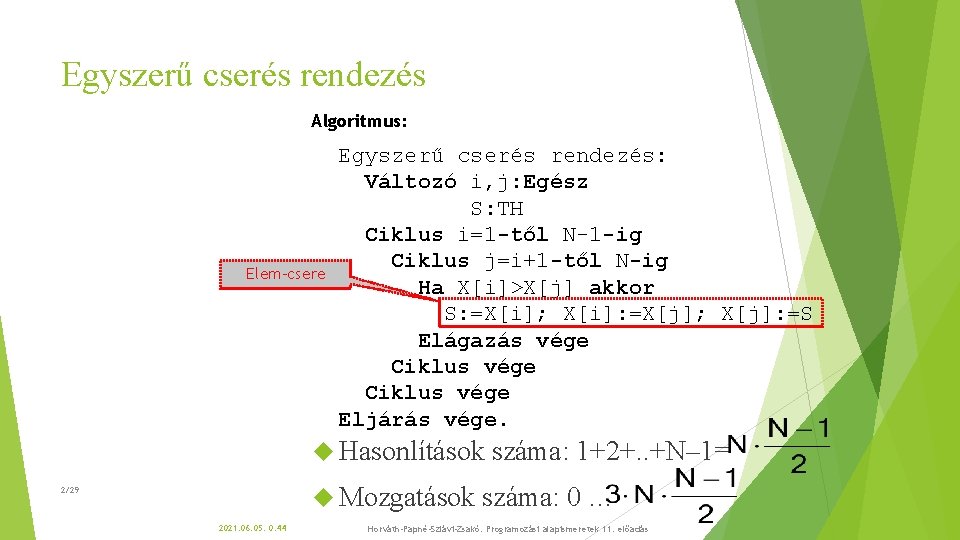
Egyszerű cserés rendezés Algoritmus: Elem-csere Egyszerű cserés rendezés: Változó i, j: Egész S: TH Ciklus i=1 -től N-1 -ig Ciklus j=i+1 -től N-ig Ha X[i]>X[j] akkor S: =X[i]; X[i]: =X[j]; X[j]: =S Elágazás vége Ciklus vége Eljárás vége. Hasonlítások Mozgatások 2/29 2021. 06. 05. 0: 44 száma: 1+2+. . +N– 1= száma: 0 … Horváth-Papné-Szlávi-Zsakó: Programozási alapismeretek 11. előadás

Minimum-kiválasztásos rendezés Algoritmus: Minimum-kiválasztásos rendezés: Minimumkiválasztás az i. től Elem-csere Változó Min. I, i, j: Egész S: TH Ciklus i=1 -től N-1 -ig Min. I: =i Ciklus j=i+1 -től N-ig Ha X[Min. I]>X[j] akkor Min. I: =j Ciklus vége S: =X[Min. I]; X[Min. I]: =X[i]; X[i]: =S Ciklus vége Eljárás vége. Hasonlítások száma: 1+2+. . +N– 1= Mozgatások 3/29 2021. 06. 05. 0: 44 száma: 3 (N– 1) Horváth-Papné-Szlávi-Zsakó: Programozási alapismeretek 11. előadás

Buborékos rendezés Algoritmus: Buborékos rendezés: Elem-csere Változó i, j: Egész S: TH Ciklus i=N-től 2 -ig -1 -esével Ciklus j=1 -től i-1 -ig Ha X[j]>X[j+1] akkor S: =X[j]; X[j]: =X[j+1]; X[j+1]: =S Elágazás vége Ciklus vége Eljárás vége. Hasonlítások Mozgatások 4/29 2021. 06. 05. 0: 44 száma: 1+2+. . +N– 1= száma: 0 … Horváth-Papné-Szlávi-Zsakó: Programozási alapismeretek 11. előadás

Javított buborékos rendezés Algoritmus: Az utolsó cserehely feljegyzé se Átírás ‘amíg’-os ciklussá 5/29 2021. 06. 05. 0: 44 Javított buborékos rendezés: Változó cs, i, j: Egész S: TH i: =N Ciklus amíg i≥ 2 cs: =0 Ciklus j=1 -től i-1 -ig Ha X[j]>X[j+1] akkor S: =X[j]; X[j]: =X[j+1]; X[j+1]: =S cs: =j Elágazás vége Ciklus vége i: =cs Ciklus vége Eljárás vége. Horváth-Papné-Szlávi-Zsakó: Programozási alapismeretek 11. előadás

Beillesztéses rendezés Algoritmus: Beillesztéses rendezés: Keresés tétel Elem-csere Változó i, j: Egész S: TH Ciklus i=2 -től N-ig j: =i-1 Ciklus amíg j>0 és X[j]>X[j+1] S: =X[j]; X[j]: =X[j+1]; X[j+1]: =S j: =j-1 Ciklus vége Eljárás vége. Ø Hasonlítások Ø Mozgatások 6/29 2021. 06. 05. 0: 44 száma: N– 1 … száma: 0 … Horváth-Papné-Szlávi-Zsakó: Programozási alapismeretek 11. előadás

Javított beillesztéses rendezés Algoritmus: Javított beillesztéses rendezés: Elem-mozgatás, nem csere! csere Változó i, j: Egész S: TH Ciklus i=2 -től N-ig S: =X[i]; j: =i-1 Ciklus amíg j>0 és X[j]>X[j+1]: =X[j]; j: =j-1 Ciklus vége X[j+1]: =S Ciklus vége Eljárás vége. Ø Hasonlítások Ø Mozgatások 7/29 2021. 06. 05. 0: 44 száma: N– 1 … száma: 2 (N– 1) … Horváth-Papné-Szlávi-Zsakó: Programozási alapismeretek 11. előadás

Számlálva szétosztó rendezés Algoritmus: Számlálva szétosztó rendezés: Db[i]: hány darab van i-ből? Megszámolás tétel Első[i]: hol az i. elsője? Rekurzív kiszámítás Változó i: Egész Db, Első: Tömb[1. . Max. N: TH] DB[1. . M]: =0 Ciklus i=1 -től N-ig Db[X[i]]: =Db[X[i]]+1 Ciklus vége Első[1]: =1 Ciklus i=1 -től M-1 -ig Első[i+1]: =Első[i]+Db[i] Ciklus vége … 8/29 2021. 06. 05. 0: 44 Horváth-Papné-Szlávi-Zsakó: Programozási alapismeretek 11. előadás

Számláló rendezés. Algoritmus: Az egyszerű cserés rendezés elvén működő számlálás. Másolás tétel Számláló rendezés: Változó i, j: Egész Db: Tömb[1. . Max. N: TH] DB[1. . M]: =0 Ciklus i=1 -től N-1 -ig Ciklus j=i+1 -től N-ig Ha X[i]>X[j] akkor Db[i]: =Db[i]+1 különben Db[j]: =Db[j]+1 Ciklus vége Ciklus i=1 -től N-ig Y[Db[i]+1]: =X[i] : = Ciklus vége Eljárás vége. Ø Hasonlítások 9/29 2021. 06. 05. 0: 44 száma: 1+2+. . +N– 1= Ø Mozgatások száma: N Ø Additív műveletek száma: ~hasonlítások Horváth-Papné-Szlávi-Zsakó: Programozási alapismeretek 11. előadás