Reminders 1 The graph of a quadratic function

Reminders (1) The graph of a quadratic function is a parabola. If a > 0 the parabola is a minimum. If a < 0 the parabola is a maximum. shaped and the turning point is

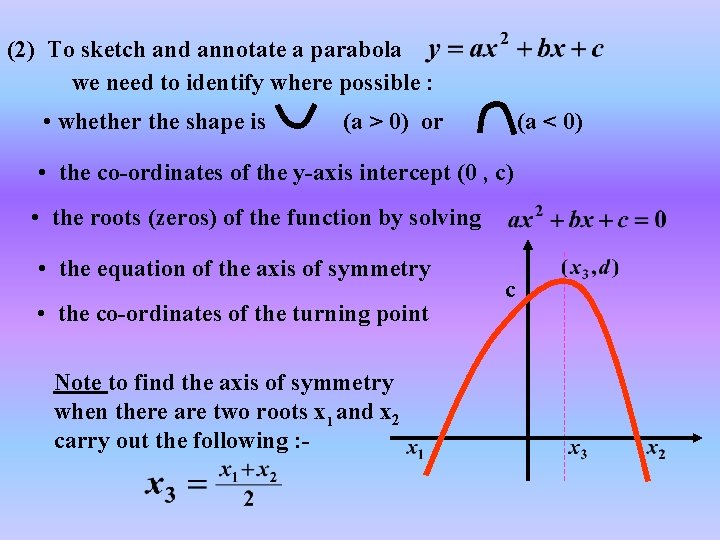
(2) To sketch and annotate a parabola we need to identify where possible : • whether the shape is (a > 0) or (a < 0) • the co-ordinates of the y-axis intercept (0 , c) • the roots (zeros) of the function by solving • the equation of the axis of symmetry • the co-ordinates of the turning point Note to find the axis of symmetry when there are two roots x 1 and x 2 carry out the following : - c

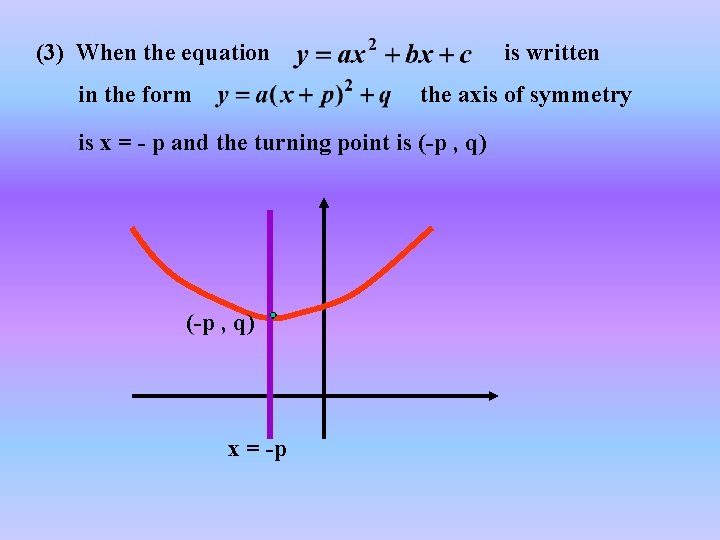
(3) When the equation in the form is written the axis of symmetry is x = - p and the turning point is (-p , q) x = -p

(4) Quadratic equations may be solved by • using the graph • factorising • completing the square • using the quadratic formula (5) (see point (5) below)

The Discriminant (Nature of the roots of a quadratic Equation) Example Solve the following equations using the quadratic formula Graphical Implications (-2)2 - 4 x (-1) = 4 - (-16) = 20 x Or Roots are given by : x Two distinct real roots

42 - 4 x 1 Graphical Implications = 16 - 16 =0 Roots are given by : x OR x (twice) One real root (repeated/equal roots)

Graphical Implications (-2)2 - 4 x 1 = 4 - 16 = -12 Roots are given by : x OR Since Ö(-12) is not a real number there are NO REAL ROOTS x

Conclusion : (i) positive 2 real roots (ii) zero 1 real root (iii) negative no real roots discriminates between real and non-real roots and so is called the DISCRIMINANT SUMMARY (i) the roots are real and distinct (unequal) TWO ROOTS (ii) (iii) the roots are real and equal ONE ROOT the roots are non-real NO ROOTS

Example 1 Determine the nature of the roots of the following equations: - (-6)2 - 4 x 1 x 8 = 36 - 32 =4 Since roots are real and distinct (-6)2 - 4 x 1 x 9 = 36 - 36 =0 Since roots are real and equal

(-6)2 - 4 x 10 = 36 - 40 = -4 Since roots are non-real Example 2 Solution For real roots Note This could be distinct roots or equal roots. 42 - 4 x 2 x p³ 0 16 - 8 p³ 0 16 ³ 8 p 8 p £ 16 p£ 2 So equation has equal roots when p£ 2

Example 3 Find the value of q so that Solution Cross-multiplying gives For equal roots So So equation has equal roots when has equal roots.

Example 4 Given that k is a real number , show that the roots of the equation are always real numbers. Solution Since therefore always real. is a square it has minimum value 0 , and so the roots of the equation

Example 5 For what values of p does the equation x 2 - 2 px + (2 - p) =0 have non-real roots? Solution x 2 - 2 px + (2 - p) =0 For non-real roots (-2 p) 2 - 4 x 1 x (2 - p) < 0 4 p 2 - 8 + 4 p < 0 4 p 2 + 4 p - 8 < 0 4(p 2 + p - 2) < 0 This is a quadratic INEQUATION. To solve this carry out the following steps : -

Step 1 Factorise the quadratic So can be written as Step 2 4(p 2 + p - 2) < 0 4(p + 2)(p - 1) < 0 Next consider solving 4(p + 2)(p - 1) = 0 So p = - 2 or Step 3 p=1 Then consider other values of p either side of these two values of p and also between these values : - setting working out in a table as follows: -

Table of Values To solve 4(p + 2)(p - 1) < 0 p (p + 2) (p - 1) 4(p + 2)(p - 1) 0 -3 + -2 0 2 1 - + 0 + + 0 - 0 + So 4(p + 2)(p - 1) < 0 for values of p in the range -2 < p < 1 So the equation has non-real roots when -2 < p < 1