Reminder Structure of a genome a gene transcription

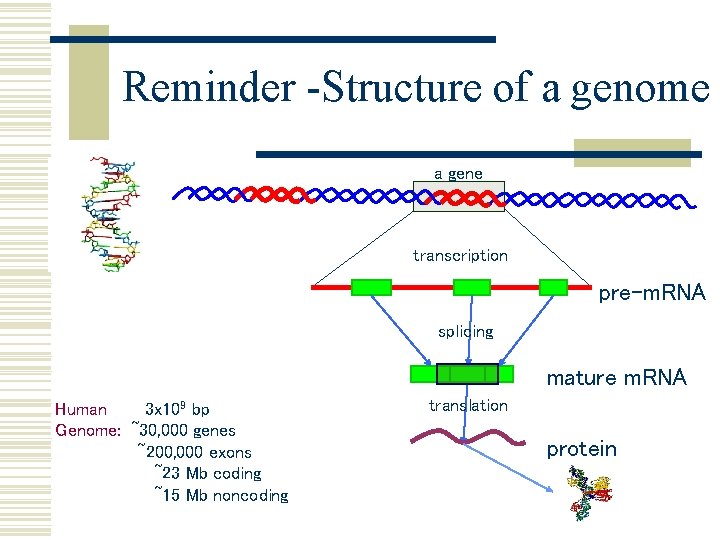
Reminder -Structure of a genome a gene transcription pre-m. RNA splicing mature m. RNA Human 3 x 109 bp Genome: ~30, 000 genes ~200, 000 exons ~23 Mb coding ~15 Mb noncoding translation protein

Sequence Alignment w We assume a link between the linear information stored in DNA, RNA or amino-acid sequence and the protein function determined by its three dimensional structure. w We want to compare the linear sequence between various genes, in order to deduce function, phylogeny, structure, origin… w The level of similarity is the homology

The Problem Biological problem Finding a way to compare and represent similarity or dissimilarity between biomolecular sequences (DNA, RNA or amino acid) Computational problem Finding a way to perform inexact or approximate matching of subsequences within strings of characters Statistical problem How to estimate the validity of our results

Course plan (for the next three weeks) w Details of biology w Estimate of computation time w Dynamic programming algorithm for full an local alignment w Statistical analysis of results w Dot matrices and heuristics for alignment w Distance matrices and information theory w (MSA)

Homology w Similarity due to descent from a common ancestor w Homologous sequences can be identified through sequence alignment w Thus, possible to predict/infer structure or function from primary sequence analysis

Gaps w Sequences may have diverged from common ancestor through mutations: n n n Substitution (AAGC AAGT) Insertion (AAG AAGT) Deletion (AAGC AAG) w Latter two operations result in gaps ( _ ) n K contiguous spaces = gap of length K ( > 0 )

Similarity and Alignment w Similarity has two aspects: n Quantitative aspect: Similarity measure l l n A number that represents degree of similarity Example: a score indicating 10% match between 2 DNA sequences. Qualitative aspect: An alignment l l a mutual arrangement of two sequences that shows where the two sequences are similar, and where they differ. An optimal alignment is one that exhibits the most correspondences, and the least differences. Example: a b c d e – h z a b wd e f h _

The Edit Distance between two strings w Definition: n The edit distance between two strings is defined as the minimum number of edit operations – insertions, deletions, & substitutions – needed to transform the first string into the second. For emphasis, note that matches are not counted. w Example: n AATT and AATG l Distance = 1 (edit operation of substitution)

String alignment w An edit transcript is a way to represent a particular transformation of one string into another n Emphasizes point mutations in the model w An alignment displays a relationship between two strings n n Global alignment means for each string, entire string is involved in the alignment Examples: (1) A A G C A AA _C_ (2) GSAQVKGHGKKVADAL …. ++ ++++H+ KV + …. NNPELQAHAGKVFKLV ….

Alignment vs. Edit Transcript w Essentially equivalent: n n n Two opposing characters in an alignment a substitution in edit transcript A gap or space in an alignment in first string an insertion of opposing character A gap or space in second string a deletion of opposing character w product vs. process

Gap cost or penalty functions w Observation: n Gap of length k more probable than k gaps of length 1 Cause might be single mutational event l Separated gaps probably arose due to different events l w Gap penalty functions: n n Linear cost: Treats both cases uniformly Common to use a higher cost for h for opening a gap and a lower cost g for extending a gap

Pairwise Sequence Alignment w Example HEAGAWGHEE PAWHEAE HEAGAWGHE-E P-A--W-HEAE --P-AW-HEAE w Which one is better?

Example A E G H W • Gap penalty: -8 A 5 -1 0 -2 -3 E -1 6 -3 0 -3 • Gap extension: -3 H -2 0 -2 10 -3 P -1 -1 -2 -2 -4 W -3 -3 15 HEAGAWGHE-E --P-AW-HEAE (-8) + (-1) + 5 + 15 + (-8) + 10 + 6 + (-8) + 6 = 9 Exercise: Calculate for HEAGAWGHE-E P-A--W-HEAE

Formal Description w Problem: Pair. Seq. Align w Input: Two sequences Scoring matrix Gap penalty Gap extension penalty x, y s d e w Output: The optimal sequence alignment

? How Difficult Is This w Given two sequences of length m and n. w How many alignments are there? f(m, n( w How many non-equivalent alignments are there ? g(m, n(

(F(n, m w F(n, m)=f(n-1, m)+f(n, m-1)+f(n-1, m-1(

(F(n, m F(n-1, m-1) F(n-1, m) F(n, m)

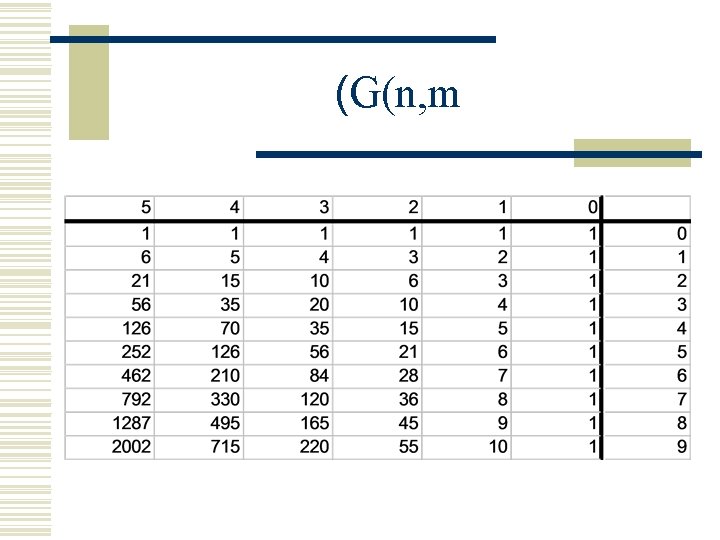
(G(n, m

(G(n, m g(n-1, m-1) g(n-1, m) g(n, m)

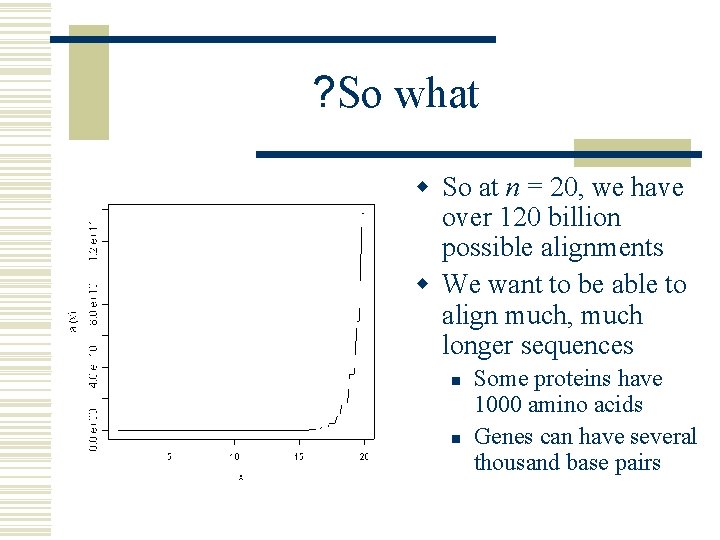
? So what w So at n = 20, we have over 120 billion possible alignments w We want to be able to align much, much longer sequences n n Some proteins have 1000 amino acids Genes can have several thousand base pairs

Dynamic Programming w General algorithmic development technique w Reuses the results of previous computations n Store intermediate results in a table for reuse w Look up in table for earlier result to build from

Global Alignment w Needleman-Wunsch 1970 w Idea: Build up optimal alignment from optimal alignments of subsequences HEAG Add score from table --P-25 HEAG- HEAGA --P-A --P— --P-A -33 Gap with bottom -33 Gap with top -20 Top and bottom

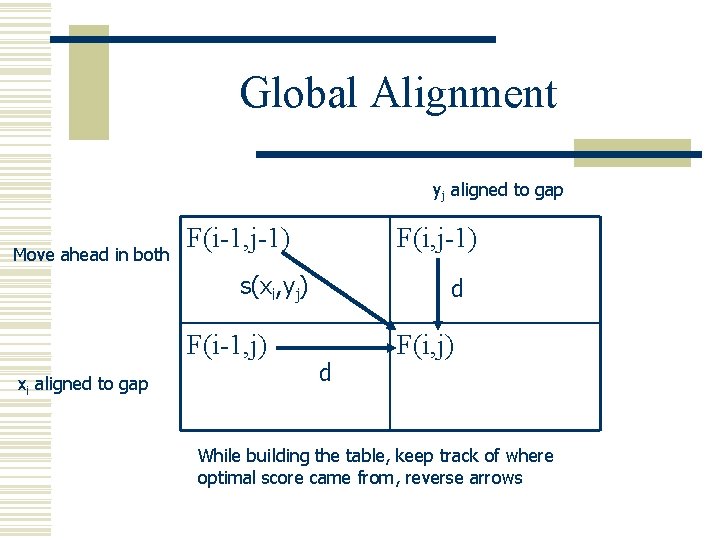
Global Alignment w Notation n n xi – ith letter of string x yj – jth letter of string y x 1. . i – Prefix of x from letters 1 through I F – matrix of optimal scores l n n F(i, j) represents optimal score lining up x 1. . i with y 1. . j d – gap penalty s – scoring matrix

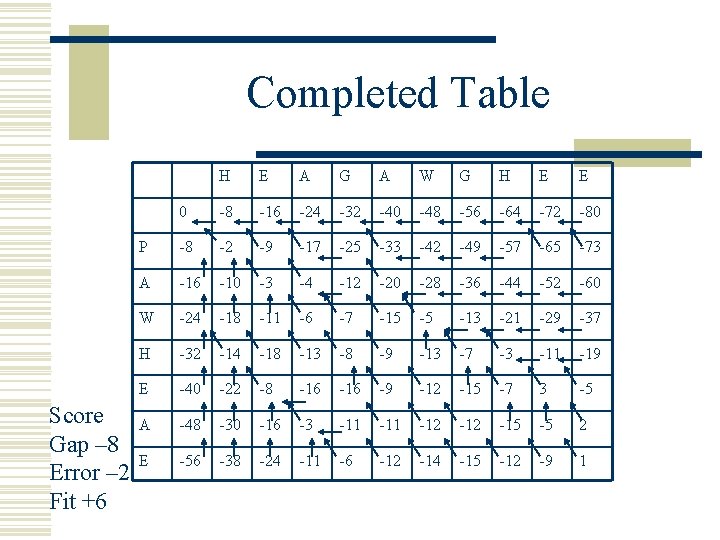
Global Alignment w The work is to build up F w Initialize: F(0, 0) = 0, F(i, 0) = id, F(0, j)=jd w Fill from top left to bottom right using the recursive relation

Global Alignment yj aligned to gap Move ahead in both F(i-1, j-1) F(i, j-1) s(xi, yj) F(i-1, j) xi aligned to gap d d F(i, j) While building the table, keep track of where optimal score came from, reverse arrows

Example H E A G A W G H E E 0 -8 -16 -24 -32 -40 -48 -56 -64 -72 -80 P -8 -2 -9 -17 -25 -33 -42 -49 -57 -65 -73 A -16 W -24 H -32 E -40 A -48 E -56

Completed Table Score Gap – 8 Error – 2 Fit +6 H E A G A W G H E E 0 -8 -16 -24 -32 -40 -48 -56 -64 -72 -80 P -8 -2 -9 -17 -25 -33 -42 -49 -57 -65 -73 A -16 -10 -3 -4 -12 -20 -28 -36 -44 -52 -60 W -24 -18 -11 -6 -7 -15 -5 -13 -21 -29 -37 H -32 -14 -18 -13 -8 -9 -13 -7 -3 -11 -19 E -40 -22 -8 -16 -9 -12 -15 -7 3 -5 A -48 -30 -16 -3 -11 -12 -15 -5 2 E -56 -38 -24 -11 -6 -12 -14 -15 -12 -9 1

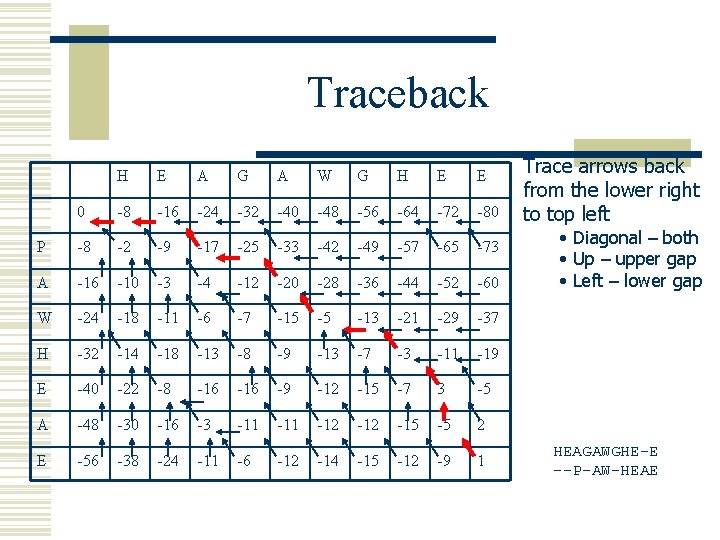
Traceback H E A G A W G H E E 0 -8 -16 -24 -32 -40 -48 -56 -64 -72 -80 P -8 -2 -9 -17 -25 -33 -42 -49 -57 -65 -73 A -16 -10 -3 -4 -12 -20 -28 -36 -44 -52 -60 W -24 -18 -11 -6 -7 -15 -5 -13 -21 -29 -37 H -32 -14 -18 -13 -8 -9 -13 -7 -3 -11 -19 E -40 -22 -8 -16 -9 -12 -15 -7 3 -5 A -48 -30 -16 -3 -11 -12 -15 -5 2 E -56 -38 -24 -11 -6 -12 -14 -15 -12 -9 1 Trace arrows back from the lower right to top left • Diagonal – both • Up – upper gap • Left – lower gap HEAGAWGHE-E --P-AW-HEAE

Summary w Uses recursion to fill in intermediate results table w Uses O(nm) space and time n n O(n 2) algorithm Feasible for moderate sized sequences, but not for aligning whole genomes.