Reliability Reliability w Reliability means repeatability or consistency

Reliability

Reliability w Reliability means repeatability or consistency w A measure is considered reliable if it would give us the same result over and over again (assuming that we are measuring isn’t changing!) IOP 301 -T Mr. Rajesh Gunesh

Definition of Reliability w Reliability usually “refers to the consistency of scores obtained by the same persons when they are reexamined with the same test on different occasions, or with different sets of equivalent items, or under other variable examining conditions (Anastasi & Urbina, 1997). w Dependable, consistent, stable, constant IOP 301 -T w Gives the same result over and over Mr. Rajesh Gunesh
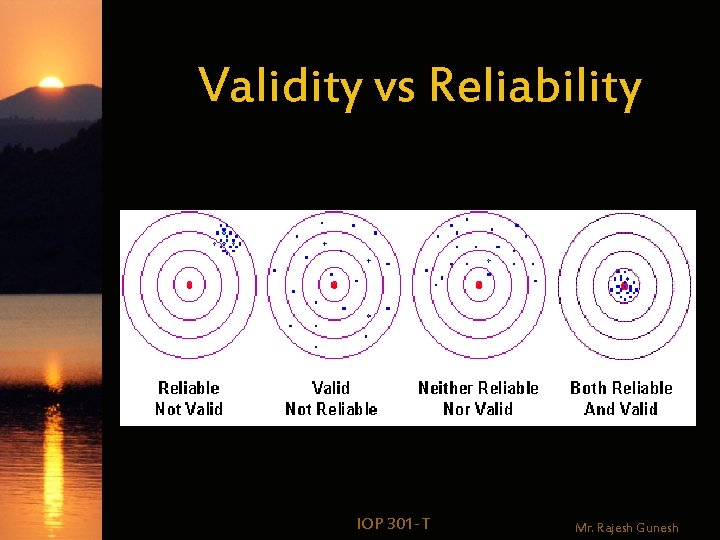
Validity vs Reliability IOP 301 -T Mr. Rajesh Gunesh

Variability and reliability w What is the acceptable error in measurement – Bathroom scale – Body thermometer – Baby weight scale – Clock with hands – Outside thermometer IOP 301 -T range of ± 1 kg ± 0. 2 C ± 20 g ± 5 min ± 1 C Mr. Rajesh Gunesh

Variability and reliability We are completely comfortable with a bathroom scale accurate to ± 1 kg, since we know that individual weights vary over far greater ranges than this, and typical changes from day to day are about the same order of magnitude. IOP 301 -T Mr. Rajesh Gunesh

Reliability w True Score Theory w Measurement Error w Theory of reliability w Types of reliability w Standard error of measurement IOP 301 -T Mr. Rajesh Gunesh
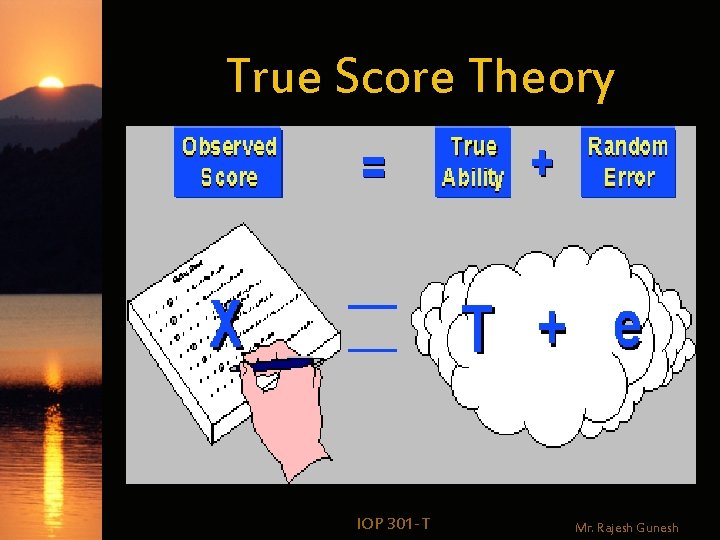
True Score Theory IOP 301 -T Mr. Rajesh Gunesh

True Score Theory w Every measurement is an additive composite of two components: 1. True ability (or the true level) of the respondent on that measure 2. Measurement error IOP 301 -T Mr. Rajesh Gunesh

True Score Theory w Individual differences in test scores – “True” differences in characteristic being assessed – “Chance” or random errors. IOP 301 -T Mr. Rajesh Gunesh

True Score Theory w What might be considered error variance in one situation may be true variance in another (e. g Anxiety) IOP 301 -T Mr. Rajesh Gunesh

Can we observe the true score? X = T + ex w We only observe the measurement, we don’t observe what’s on the right side of equation (only God knows what those values are) IOP 301 -T Mr. Rajesh Gunesh

True Score Theory var(X) = var(T) + var(ex) w The variability of the measure is the sum of the variability due to true score and the variability due to random error IOP 301 -T Mr. Rajesh Gunesh

What is error variance? Conditions irrelevant to purpose of the test – Environment (e. g. , quiet v. noisy) – Instructions (e. g. , written v. verbal) – Time limits (e. g. , limited v. unlimited) – Rapport with test taker IOP 301 -T Mr. Rajesh Gunesh

Measurement Error w. Measurement error: –Random –Systematic IOP 301 -T Mr. Rajesh Gunesh

Measurement Error IOP 301 -T Mr. Rajesh Gunesh

Measurement Error w Random error: effects are NOT consistent across the whole sample, they elevate some scores and depress others – Only adds noise; does not affect mean score IOP 301 -T Mr. Rajesh Gunesh

Measurement Error w Systematic error: effects are generally consistent across a whole sample – Example: environmental conditions for group testing (e. g. , temperature of the room) – Generally either consistently positive (elevate scores) or negative (depress scores) IOP 301 -T Mr. Rajesh Gunesh

Measurement Error IOP 301 -T Mr. Rajesh Gunesh
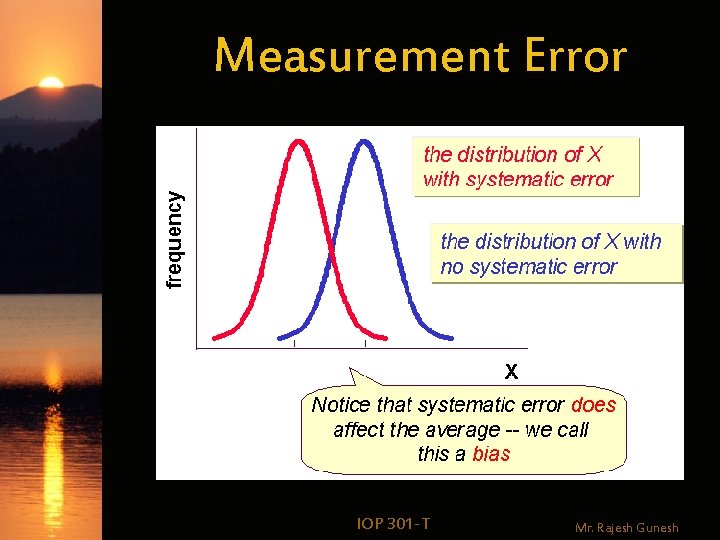
Measurement Error IOP 301 -T Mr. Rajesh Gunesh

Theory of Reliability IOP 301 -T Mr. Rajesh Gunesh

Reliability The variance of the true Reliability = score The variance of the measure Reliability = IOP 301 -T Var(T) Var(X) Mr. Rajesh Gunesh

How big is an estimate of Reliability? Reliability = Subject variability + measurement error Reliability = Var(T) Var(X) IOP 301 -T = Var(T) + Var(e) Mr. Rajesh Gunesh

w We can’t compute reliability because we can’t calculate the variance of the true score; but we can get an estimate of the variability. IOP 301 -T Mr. Rajesh Gunesh

Estimate of Reliability w Observations would be related to each other to the degree that they share true scores. For example consider the correlation between X 1 and X 2: IOP 301 -T Mr. Rajesh Gunesh
IOP 301 -T Mr. Rajesh Gunesh

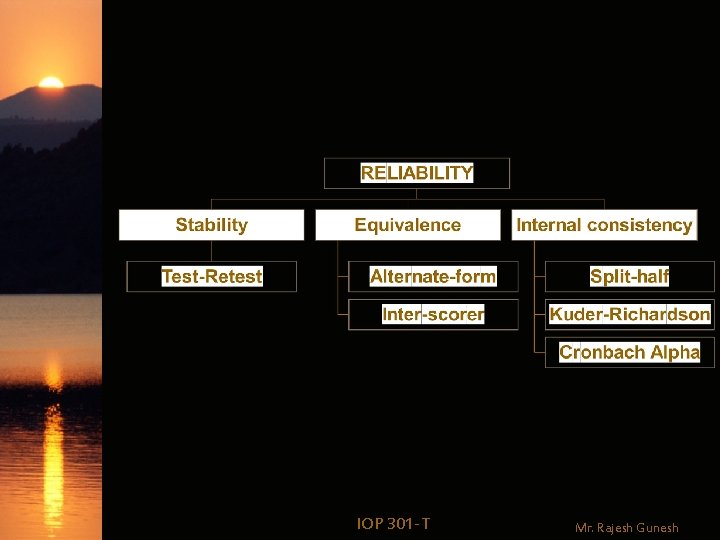
Types of Reliability 1. Test-Retest Reliability Used to assess the consistency of a measure from one time to another 2. Alternate-form Reliability Used to assess the consistency of the results of two tests constructed the same way from the same content domain IOP 301 -T Mr. Rajesh Gunesh

Types of Reliability 3. Split-half Reliability Used to assess the consistency of results across items within a test by splitting them into two equivalent halves Ø Kuder-Richardson Reliability Used to assess the extent to which items are homogenous when items have a dichotomous response, e. g. “yes/no” items. IOP 301 -T Mr. Rajesh Gunesh

Types of Reliability Ø Cronbach’s alpha (α) Reliability Compares the consistency of response of all items on the scale (Likert scale or linear graphic response format) 4. Inter-Rater or Inter-Scorer Reliability Used to assess the concordance between two or more observers scores of the same event or IOP 301 -T for phenomenon observational Mr. Rajesh Gunesh

Test-Retest Reliability w Definition: When the same test is administered to the same individual (or sample) on two different occasions IOP 301 -T Mr. Rajesh Gunesh

Test-Retest Reliability: Used to assess the consistency of a measure from one time to another IOP 301 -T Mr. Rajesh Gunesh

Test-Retest Reliability w Statistics used – Pearson r or Spearman rho w Warning – Correlation decreases over time because error variance INCREASES (and may change in nature) – Closer in time the two scores were obtained, the more the factors which contribute to error variance are the same IOP 301 -T Mr. Rajesh Gunesh

Test-Retest Reliability w Warning – Circumstances may be different for both test-taker and physical environment. – Transfer effects like practice and memory might play a role on the second testing occasion IOP 301 -T Mr. Rajesh Gunesh

Alternate-form Reliability w Definition: Two equivalent forms of the same measure administered to the same group on two different occasions IOP 301 -T Mr. Rajesh Gunesh
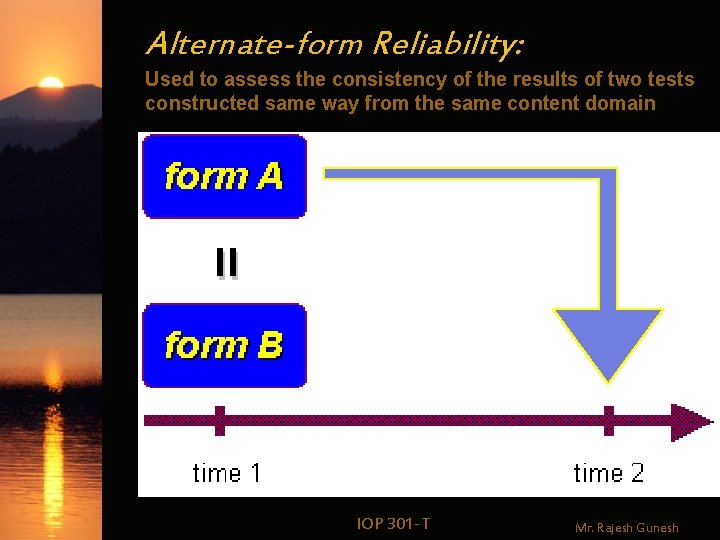
Alternate-form Reliability: Used to assess the consistency of the results of two tests constructed same way from the same content domain IOP 301 -T Mr. Rajesh Gunesh

Alternate-form Reliability w Statistic used – Pearson r or Spearman rho w Warning – Even when randomly chosen, the two forms may not be truly parallel – It is difficult to construct equivalent tests IOP 301 -T Mr. Rajesh Gunesh

Alternate-form Reliability w Warning – Even when randomly chosen, the two forms may not be truly parallel – It is difficult to construct equivalent tests – The tests should have the same number of items, same scoring procedure, uniform content and item difficulty level IOP 301 -T Mr. Rajesh Gunesh

Split-half Reliability w Definition: Randomly divide the test into two forms; calculate scores for Form A, B; calculate Pearson r as index of reliability IOP 301 -T Mr. Rajesh Gunesh
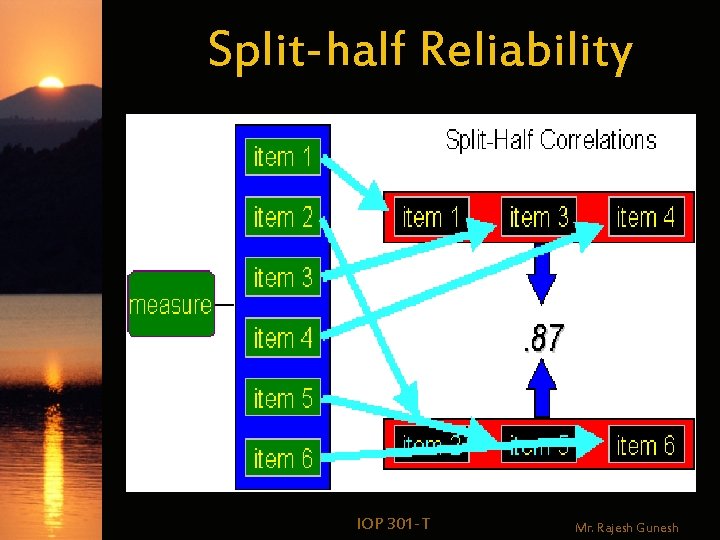
Split-half Reliability IOP 301 -T Mr. Rajesh Gunesh

Split-half Reliability (Spearman-Brown formula) IOP 301 -T Mr. Rajesh Gunesh

Split-half Reliability w Warning The correlation between the odd and even scores are generally an underestimation of the reliability coefficient because it is based only on half the test. IOP 301 -T Mr. Rajesh Gunesh

Cronbach’s alpha & Kuder-Richardson-20 Measures the extent to which items on a test are homogeneous; mean of all possible split-half combinations – Kuder-Richardson-20 (KR-20): for dichotomous data – Cronbach’s alpha: for nondichotomous data IOP 301 -T Mr. Rajesh Gunesh
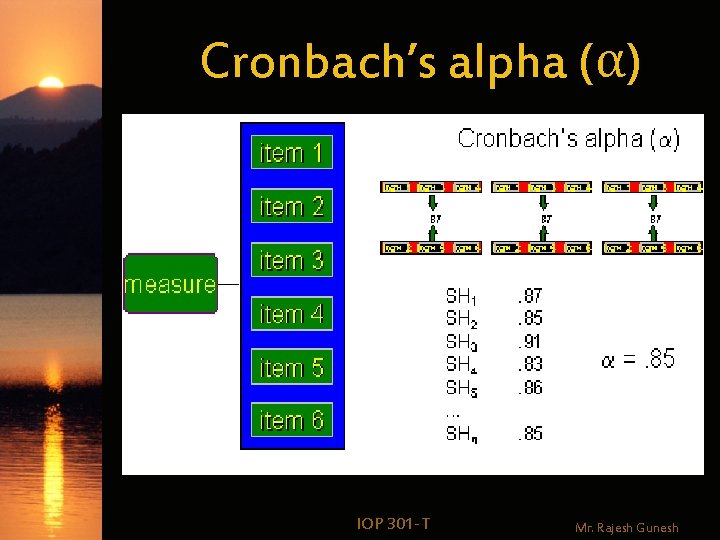
Cronbach’s alpha (α) IOP 301 -T Mr. Rajesh Gunesh

Cronbach’s alpha (α) (Coefficient alpha) IOP 301 -T Mr. Rajesh Gunesh

Kuder-Richardson (KR 20) IOP 301 -T Mr. Rajesh Gunesh
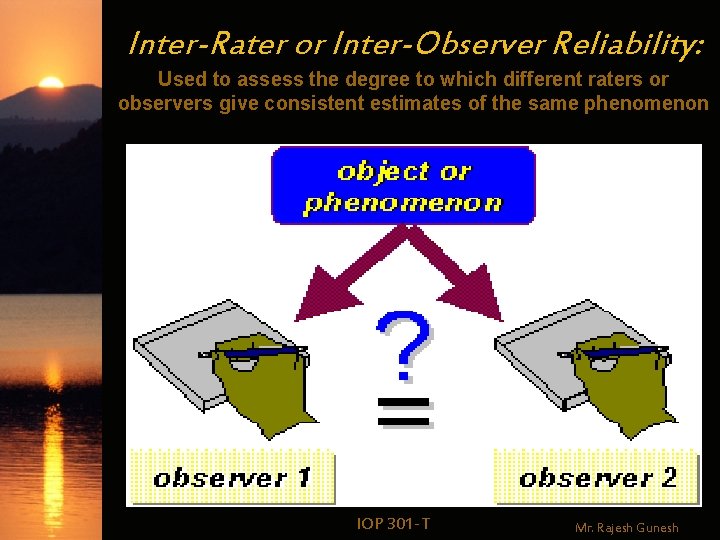
Inter-Rater or Inter-Observer Reliability: Used to assess the degree to which different raters or observers give consistent estimates of the same phenomenon IOP 301 -T Mr. Rajesh Gunesh

Inter-rater Reliability w. Definition Measures the extent to which multiple raters or judges agree when providing a rating of behavior IOP 301 -T Mr. Rajesh Gunesh

Inter-rater Reliability w Statistics used – Nominal/categorical data • Kappa statistic – Ordinal data • Kendall’s tau to see if pairs of ranks for each of several individuals are related – Two judges rate 20 elementary school children on an index of hyperactivity and rank order them IOP 301 -T Mr. Rajesh Gunesh

Inter-rater Reliability w Statistics used – Interval or ratio data • Pearson r using data obtained from the hyperactivity index IOP 301 -T Mr. Rajesh Gunesh

Factors affecting Reliability w Whether a measure is speeded w Variability in individual scores w Ability level IOP 301 -T Mr. Rajesh Gunesh

Whether a measure is speeded For speeded measures, test-retest and equivalent-form reliability are more appropriate. Split-half techniques may be considered if the split occurs according to time rather than number of items. IOP 301 -T Mr. Rajesh Gunesh

Variability in individual scores Correlation is normally affected by the range of individual differences in a group. Sometimes, smaller subgroups display correlation coefficients which are completely different from that of the whole group. This phenomenon is known as range restriction. IOP 301 -T Mr. Rajesh Gunesh

Ability level One must also consider the variability and ability levels of samples. It is advisable to compute separate reliability coefficients for homogeneous and heterogeneous subgroups. IOP 301 -T Mr. Rajesh Gunesh

Interpretation of Reliability One must ask oneself the following questions: ØHow high must the coefficient of reliability be? ØHow is it interpreted? ØWhat is the standard error of measurement? IOP 301 -T Mr. Rajesh Gunesh

Magnitude of reliability coefficient Anastasi & Urbina(1997) 0. 8 – 0. 9 Huysamen (1996) at least 0. 85 for individuals at least 0. 65 for groups Smit (1996) 0. 8 – 0. 85 for personality & interest at least 0. 9 IOPfor aptitude 301 -T Mr. Rajesh Gunesh

Standard Error of the Measurement w Definition: Estimate of the amount of error usually attached to an individual’s obtained test score – As SEM ↑, test reliability ↓ – As SEM ↓, test reliability ↑ IOP 301 -T Mr. Rajesh Gunesh

Standard Error of the Measurement IOP 301 -T Mr. Rajesh Gunesh

Standard Error of the Measurement w Confidence Interval: Uses SEM to calculate a band or range of scores that has a high probability of including the person’s true score. w Example: 95% confidence interval means only 5 times in 100 will the person’s TRUE score lie outside this range of scores. IOP 301 -T Mr. Rajesh Gunesh

Reliability w Formula: CI = Obtained score + z(SEM) z = 1. 0 for 68% level z = 1. 44 for 85% level z = 1. 65 for 90% level z = 1. 96 for 95% level z = 2. 58 for 99% level IOP 301 -T Mr. Rajesh Gunesh

Reliability of standardized tests w An acceptable standardized test should have reliability coefficients of at least: Ø 0. 95 for internal consistency Ø 0. 90 for test-retest (stability) Ø 0. 85 for alternate-forms (equivalency IOP )301 -T Mr. Rajesh Gunesh

Reliability: Implications w Evaluating a test – What types of reliability have been calculated and with what samples? – What are the strengths of the reliability coefficients? – What is the SEM for a test score – How does this information influence decision to use and interpret test scores? IOP 301 -T Mr. Rajesh Gunesh
- Slides: 61