Reliability Reliability Reliability The confidence that an emergency

Reliability

Reliability • Reliability: The confidence that an emergency system will function as planned when the next large-scale incident or disaster occurs. – “Evaluating the Reliability of Emergency Response Systems for Large-Scale Incident Operations, “ Brian A. Jackson, Kay Sullivan Faith, Henry H. Willis, RAND Corporation, 2010. •

Reliability • Availability: the proportion of time a system is in a functioning condition. • Resilience: the capability of an asset, system, or network to maintain its function during or to recover from a terrorist attack or other incident. – (DHS, National Infrastructure Protection Plan 2006, p. 104)

Emergency Reliability Applications • Human response • Emergency Support Functions (ESFs) – Emergency medicine – Communications systems • Critical Infrastructure – Energy, particularly electrical – Transportation systems • Equipment

References • Critical Infrastructure: Systems and assets, whether physical of virtual, so vital to the United States that the incapacity or destruction of such systems and assets would be a debilitating impact on security, national economic security, national public health or safety, or any combination of those matters • Source: USA Patriot Act, Sec. 1016(e).

References • Emergency Support Functions (ESFs): Used by the Federal Government and many State governments as the primary mechanism at the operational level to organize and provide assistance. ESFs align categories of resources and provide strategic objectives for their use. ESFs utilize standardized resource management concepts such as typing, inventorying, and tracking to facilitate the dispatch, deployment, and recovery of resources before, during, and after an incident. • Source: NRF Resource Center.

Emergency System Requisites • The system must have the necessary components to respond. • The system components must be configured to allow the system to achieve its goals. • The system must operate without error.

Economic View of Reliability • Highly reliable systems are expensive • Failures are rare but very expensive • How do we design systems that reduce failure rates and are not expensive? • How much reliability is enough? • How do we improve the reliability of an existing system?

Reliability Examples • Redundant Power Supplies/Sources

Reliability Assessment • Reliability (R) is the probability that a system will operate in the next instant. • Scientifically, we measure reliability by testing to failure some sufficient number of instances of the system until they fail.

Reliability Assessment • Emergency systems are typically so large and diverse that it is economically and logistically infeasible to test them. • It is unethical to create an emergency merely to test an emergency system. • An emergency response system implementation is usually unique. It is designed for a particular application, location, performance and environment. Thus, comparable data from similar emergency systems is unlikely to exist. • Citizens are seldom worried about the reliability of the emergency response system as a whole. They are only concerned with the reliability of that portion of the system which is used to service their request. • Emergency response systems are loosely coupled combinations of links and processors. Portions of the emergency response system can fail without having a significant impact on the rest of the system.

Reliability Assessment • We can, however, practically test components of systems for their reliabilities – Beams, materials, computers, links, etc. • What we need is some way to estimate the reliability of a system R from the reliabilities of its components ri.

System Architectures • Series • Parallel • Hybrid

Components • Fully Redundant • Partially Redundant

Series System Example • Electrical Power System
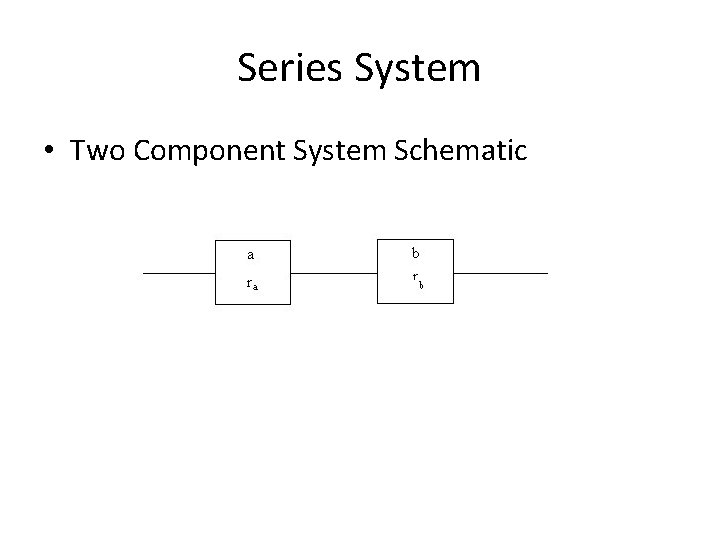
Series System • Two Component System Schematic

Series System • How do we estimate the System Reliability from the component reliabilities ra and rb? – R = f(ra, rb) • System Failure Rate –F=1 -R • Component Failure Rate – fa = 1 - r a

Reliability Assumptions • A component is either failed or operating; there are no partial component malfunctions. • A single component failure does not cause other components to fail. In other words, each component operates independently.

Two Component System Behavior Component System a b Probability State Working ra * r b Operating Working Failed ra * (1 - rb) Not Operating Failed Working ( 1 - r a ) * rb Not Operating Failed ( 1 - ra) * (1 - rb) Not Operating

Two Component Series System Reliability • Two Components – The system operates only when each of the components is working – R = r a* r b

Series System Example • Two Component System Schematic

Two Component Series System Reliability • Two Components Example – R = r a* r b – R =. 9 *. 8 – R=. 72

Series System • Three Component System Schematic

Three Component System Behavior Component System a b c Probability State Working ra * rb * rc Operating Working Failed ra * rb * (1 - rc) Not Operating Working Failed Working ra * ( 1 - rb) * rc Not Operating Working Failed ra * ( 1 - rb) * ( 1 - rc) Not Operating Failed Working ( 1 - ra) * rb * rc Not Operating Failed Working Failed ( 1 - ra) * rb * (1 rc) Not Operating Failed ( 1 - ra) * (1 - rb) * (1 - rc) Not Operating

Three Component Series System Reliability • Three Components – The system operates only when each of the components is working – R = r a* r b * r c

Series System Reliability • General – R = r a * rb * rc *. . . r n • For identical reliability components – R = rn
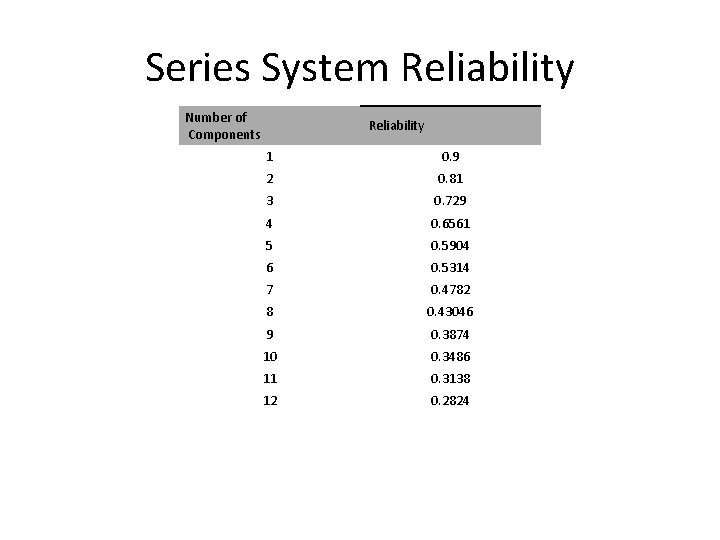
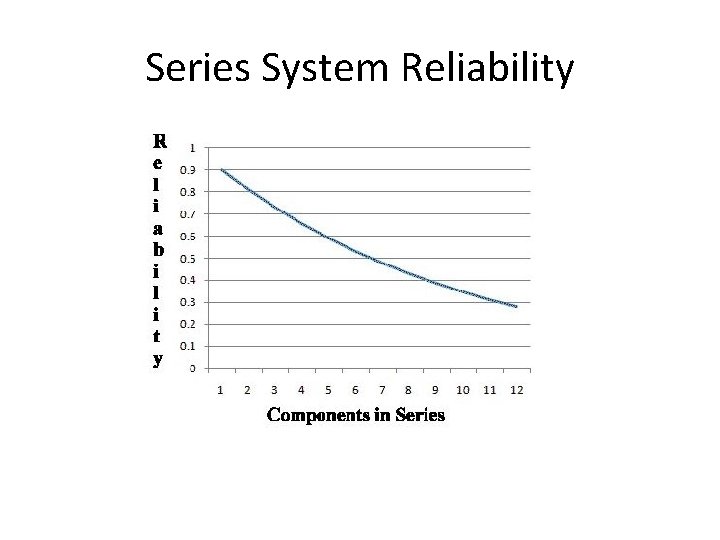
Series System Reliability Number of Components Reliability 1 0. 9 2 0. 81 3 0. 729 4 0. 6561 5 0. 5904 6 0. 5314 7 0. 4782 8 0. 43046 9 0. 3874 10 0. 3486 11 0. 3138 12 0. 2824
Series System Reliability

Series System Reliability • Observations – Adding series components to a system makes that system less reliable. R << Rold * rnew – A series system's reliability is less than the reliability of the system's least reliable component. R << rmin
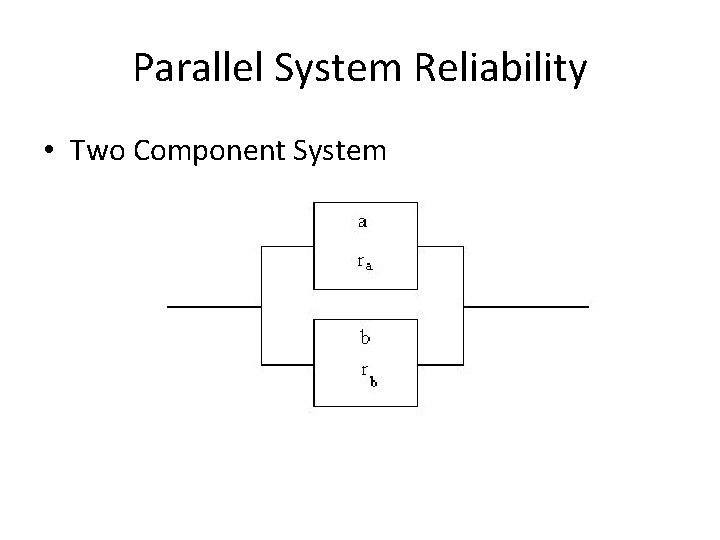
Parallel System Reliability • Two Component System

Two Component System Behavior a b Probability State Working ra * r b Operating Working Failed ra * (1 - rb) Operating Failed Working ( 1 - r a ) * rb Operating Failed ( 1 - ra) * (1 rb) Not Operating

Two Component Parallel System Reliability • Two Components – The system operates when one of the components is working – R = ra* rb + ra* (1 - rb ) + (1 - ra ) * rb
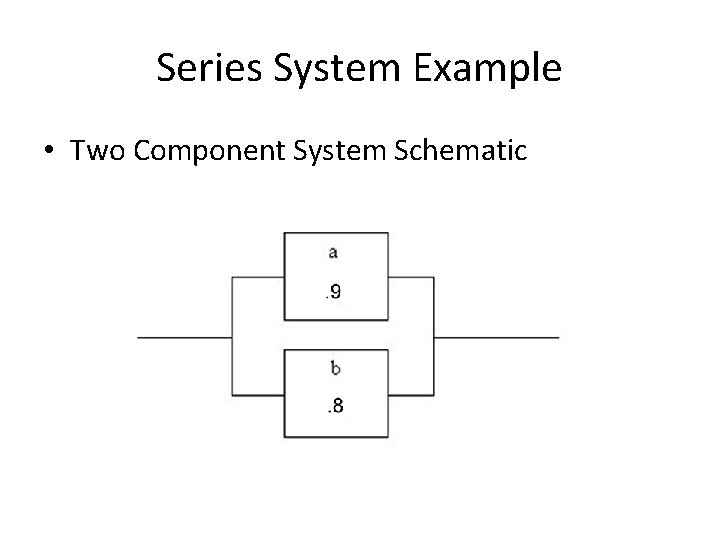
Series System Example • Two Component System Schematic

Two Component Series System Reliability • Two Components Example – R = ra* rb + ra* (1 - rb ) + (1 - ra ) * rb – R =. 9 *. 8 +. 9 *. 2 +. 1 *. 8 – R=. 98
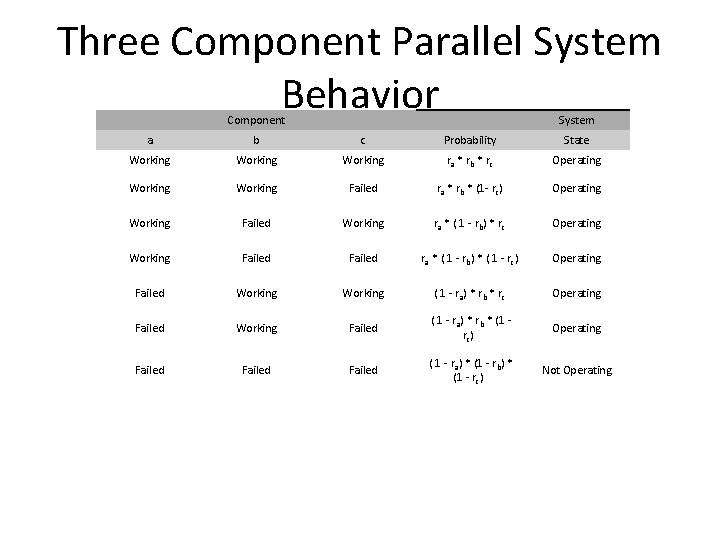
Three Component Parallel System Behavior Component System a b c Probability State Working ra * rb * rc Operating Working Failed ra * rb * (1 - rc) Operating Working Failed Working ra * ( 1 - rb) * rc Operating Working Failed ra * ( 1 - rb) * ( 1 - rc) Operating Failed Working ( 1 - ra) * rb * rc Operating Failed Working Failed ( 1 - ra) * rb * (1 rc) Operating Failed ( 1 - ra) * (1 - rb) * (1 - rc) Not Operating

Three Component Parallel System Reliability • Three Components – The system operates only when any one of the components is working • R = ra* rb * rc + ra * rb * (1 - rc) + ra * ( 1 - rb) * rc + r a * ( 1 - r b ) * ( 1 - r c ) + ( 1 - r a) * r b * r c + ( 1 ra) * rb * (1 - rc)

Parallel System Reliability • General – R = 1 - Π i ( 1 - r i) • For identical reliability components – R = 1 - ( 1 - r )n
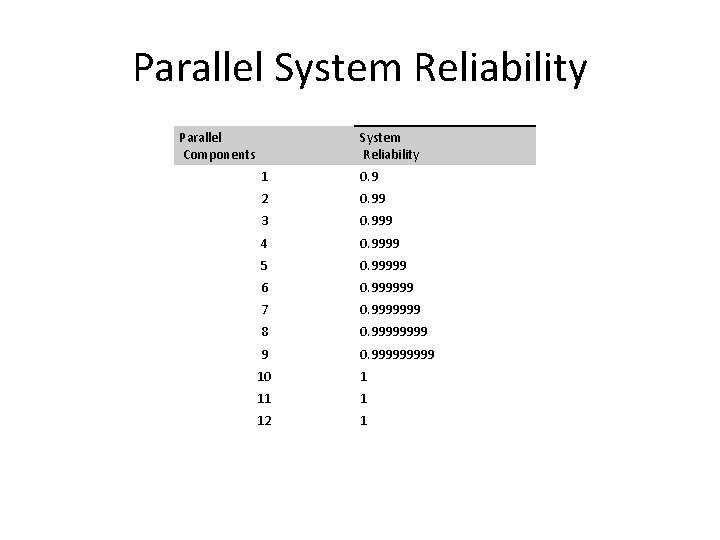
Parallel System Reliability Parallel Components System Reliability 1 0. 9 2 0. 99 3 0. 999 4 0. 9999 5 0. 99999 6 0. 999999 7 0. 9999999 8 0. 9999 9 0. 99999 10 1 11 1 12 1
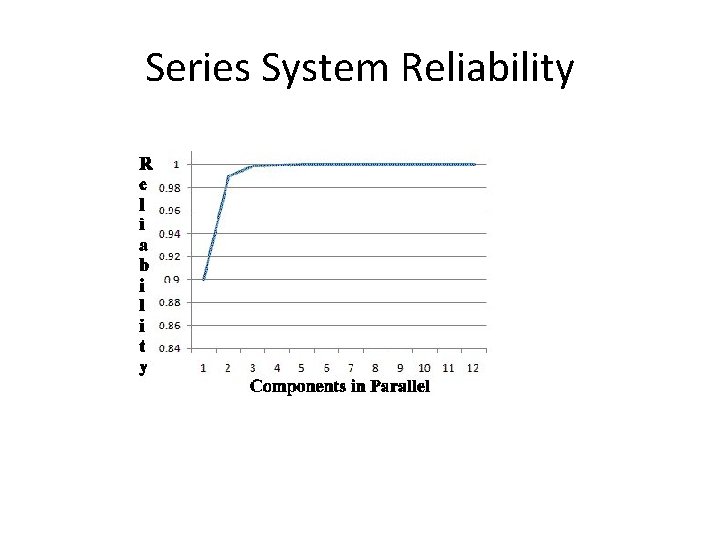
Series System Reliability

Parallel System Reliability • Observations – Adding parallel components to a system increases the reliability of the system, often referred to as redundancy. R >> 1 - Σ i * ( 1 - ri ) * ( 1 - rnew ) – The reliability of a purely parallel system is greater than the reliability of the system's most reliable component. R >> rmax
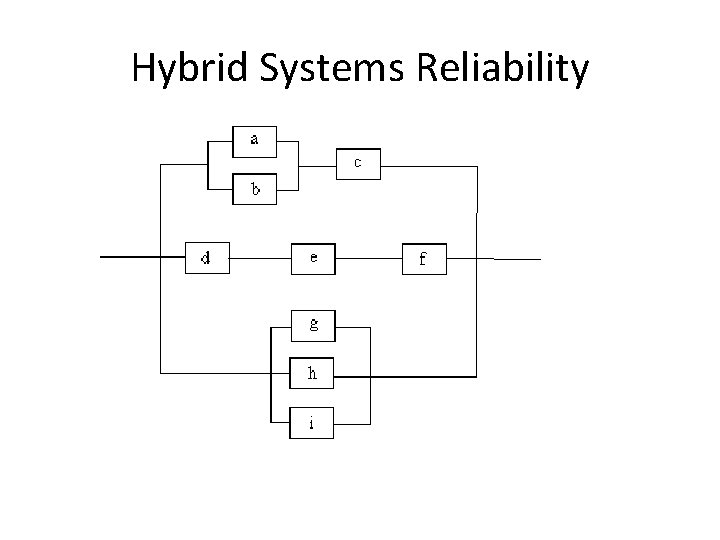
Hybrid Systems Reliability
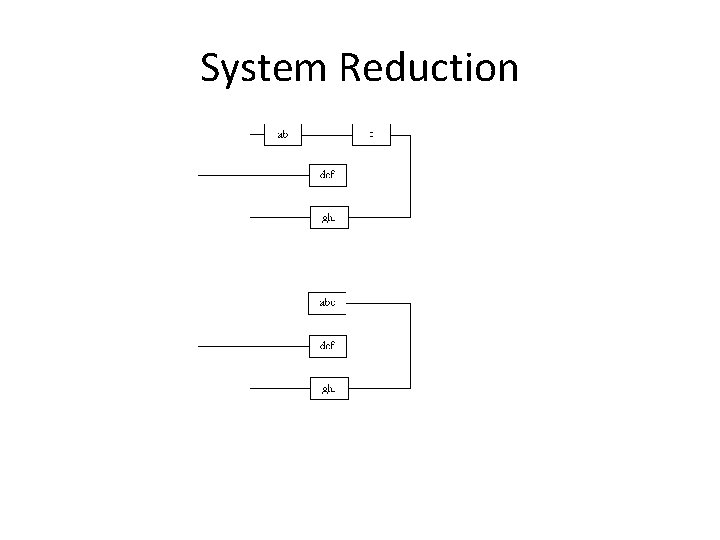
System Reduction

Example Emergency Routing • How do I assess the reliability of a person’s evacuating Washington DC to Harrisburg, PA?
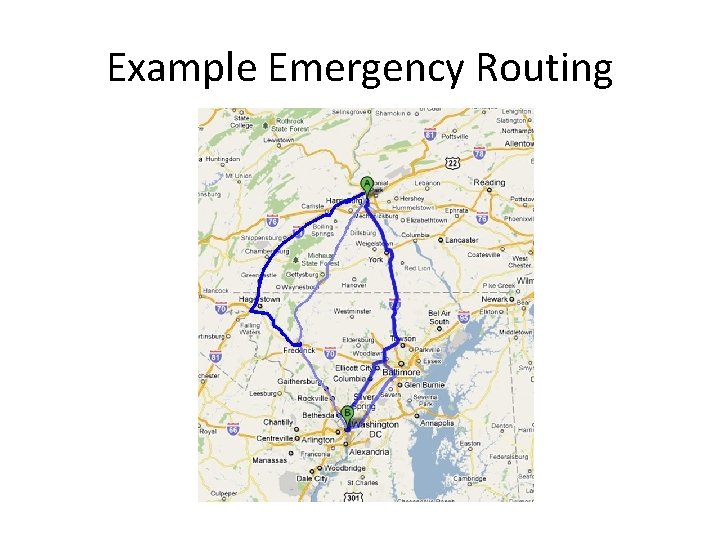
Example Emergency Routing
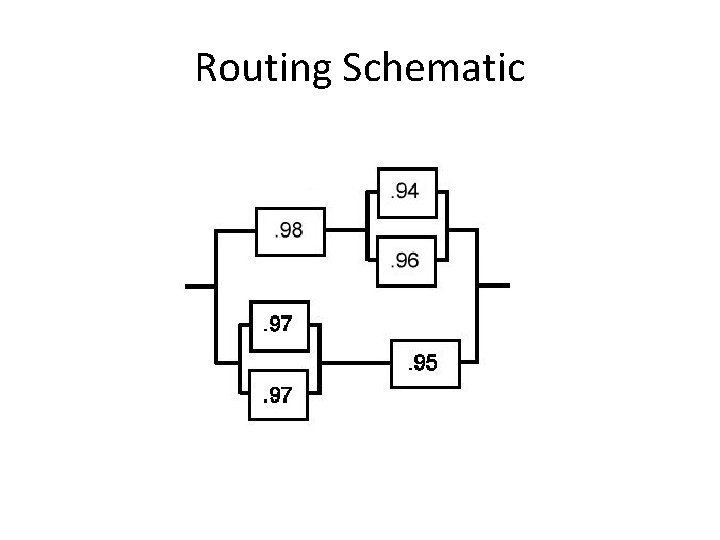
Routing Schematic
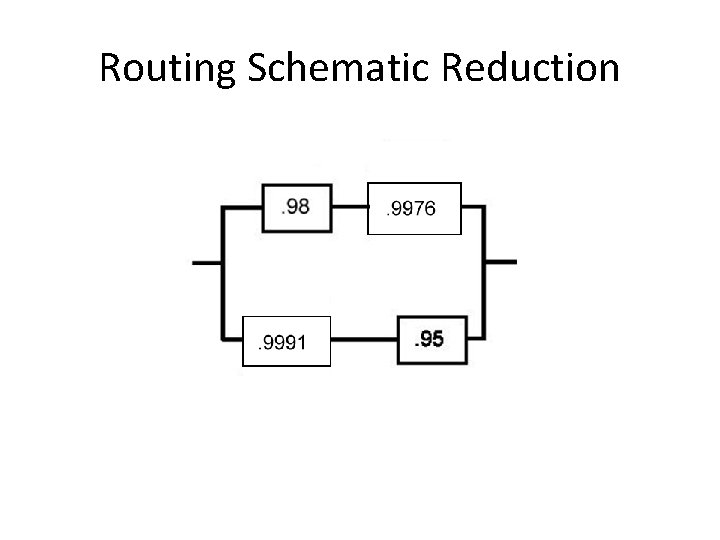
Routing Schematic Reduction
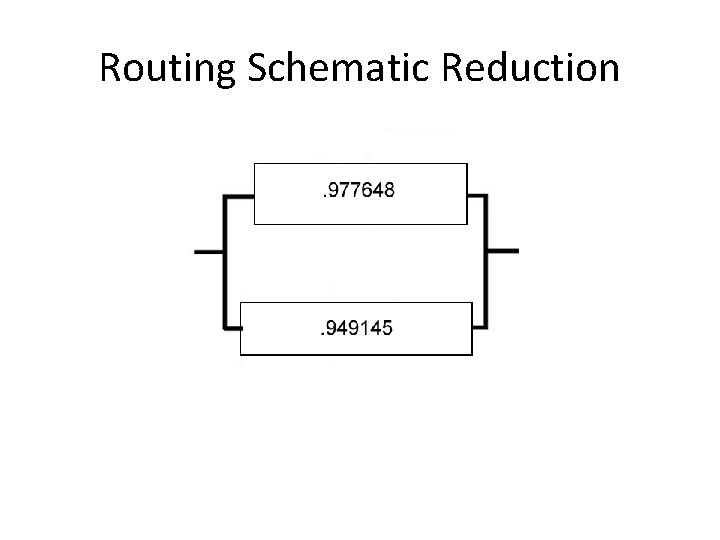
Routing Schematic Reduction

Routing Schematic Reduction

n of N Parallel Component Reliability Rn/N • What happens if the components are not completely redundant? • For a system of N parallel components, n or more of them must be working for the system to operate. • We can use components of lower capacity and they ought to be less expensive

Three Component Parallel System Behavior Component System a b c Probability State Working ra * rb * rc Operating Working Failed ra * rb * (1 - rc) Operating Working Failed Working ra * ( 1 - rb) * rc Operating Working Failed ra * ( 1 - rb) * ( 1 - rc) Operating Failed Working ( 1 - ra) * rb * rc Operating Failed Working Failed ( 1 - ra) * rb * (1 rc) Operating Failed ( 1 - ra) * (1 - rb) * (1 - rc) Not Operating

n of N Parallel Component Reliability Rn/N • R 3/3 = ra * rb * rc • R 2/3 = ra * rb * rc + (3 operate) ra * r b * ( 1 - r c ) + ra * ( 1 - r b ) * r c + ( 1 - ra ) * rb * rc (2 operate) • R 1/3 = ra * rb * rc + (3 operate) ra * r b * ( 1 - r c ) + ra * ( 1 - r b ) * r c + ( 1 - ra ) * rb * rc + (2 operate) ra * ( 1 - r b ) * ( 1 - r c ) + ( 1 - r a ) * rb * ( 1 - r c ) + ( 1 - ra ) * ( 1 - rb ) * rc (1 operates)

n of N Parallel Component Reliability Rn/N • R 3/3 Same as Series System • R 1/3 Same as Parallel System • R 1/3 = R 2/3 = R 3/3

n of N Parallel Component Reliability Rn/N • Generalization – Rn/N = ΣNn. Cn. Nri(1 -r)N-I – Where Ci. K is the number of combinations in K components taken i at a time or: Ci. K = K!/(i! (K-i)!) for 0 <= i <= K

n of N Parallel Component Reliability Rn/N • Example: – Six component system – Each has a reliability of. 95 – Four or more must be working for the system to operate at capacity

n of N Parallel Component Reliability Rn/N • R 4/6 = C 46 * (. 95 )4 * (. 05 )2 + C 56 * (. 95 )5 * (. 05 ) + C 66 * (. 95 )6 * (. 05 )0 15 * (. 95 )4 * (. 05 )2 + 6 * (. 95 )5 * (. 05 ) + 1 * (. 95 )6 * (. 05 )0. 030544 +. 232134 +. 735092 =. 99777
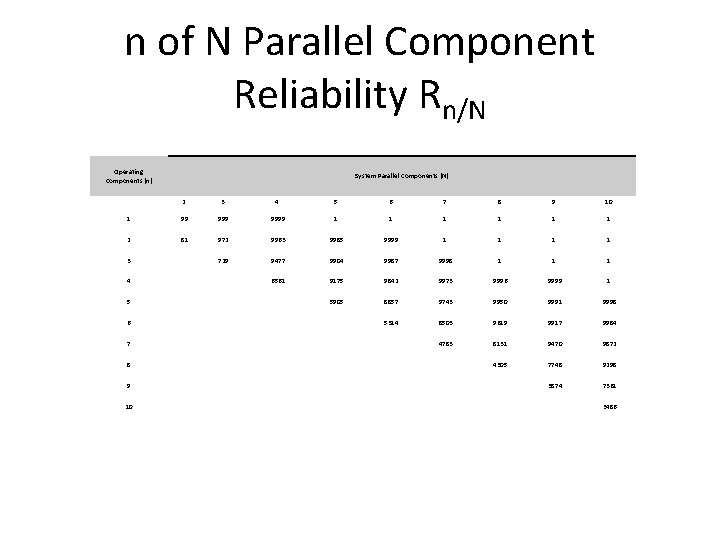
n of N Parallel Component Reliability Rn/N Operating Components (n) System Parallel Components (N) 2 3 4 5 6 7 8 9 10 1 . 9999 1 1 1 2 . 81 . 972 . 9963 . 9985 . 9999 1 1 . 729 . 9477 . 9904 . 9987 . 9998 1 1 1 . 6561 . 9175 . 9842 . 9973 . 9996 . 9999 1 . 5905 . 8857 . 9743 . 9950 . 9991 . 9998 . 5314 . 8503 . 9619 . 9917 . 9984 . 4783 . 8131 . 9470 . 9872 . 4305 . 7748 . 9298 . 3874 . 7361 3 4 5 6 7 8 9 10 . 3486
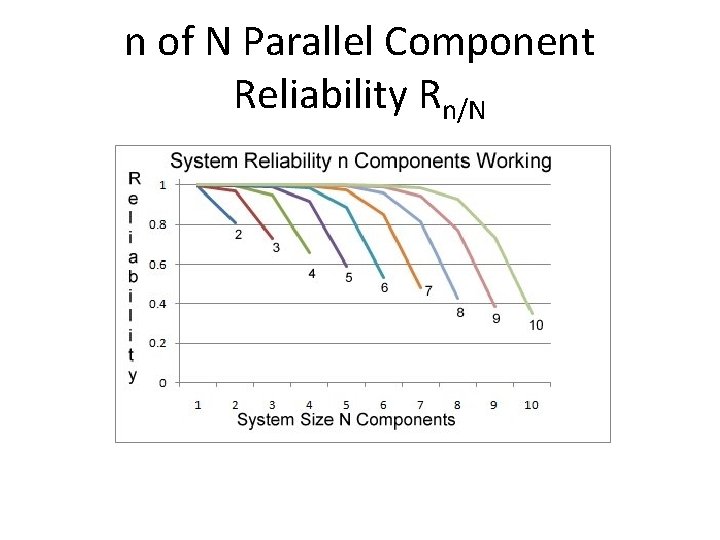
n of N Parallel Component Reliability Rn/N

Reliability Design • Use components that are inherently more reliable. • Add parallel components.

Reliability Design • How much reliability is enough? • How much reliability can I afford? • What is the optimum (minimum) cost?
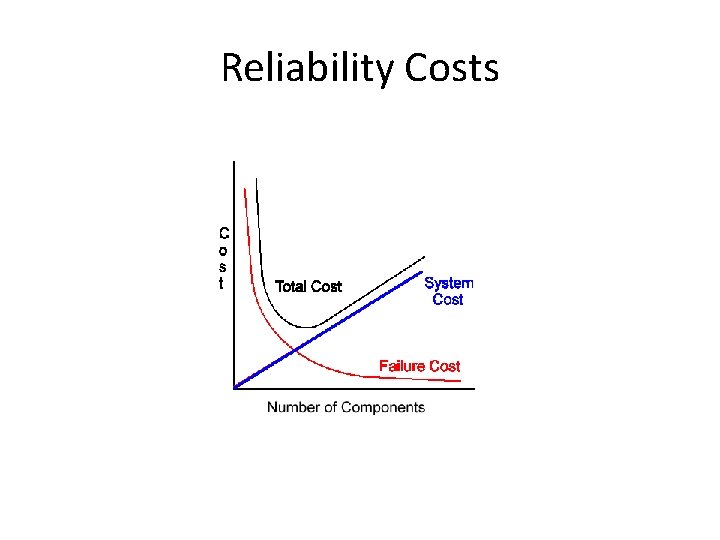
Reliability Costs

Reliability Costs • TC – total system reliability cost • TS – costs to make the system reliable • TF – the cost associated with the system having a failure

Variables • n – Number of system components • Cc – Cost of an individual component • Cf – Cost of a failure • F – Failure probability ( F = 1 - R)

Reliability Costs • TC = TS + TF • TS = n * Cc • TF = F * Cf •

Example Parallel System • F = ( 1 - r )n • TC = n * Cc + ( 1 - r )n * Cf

Example Parallel System • Component costs = $100 • Component Reliability =. 9 • Failure cost = $5000
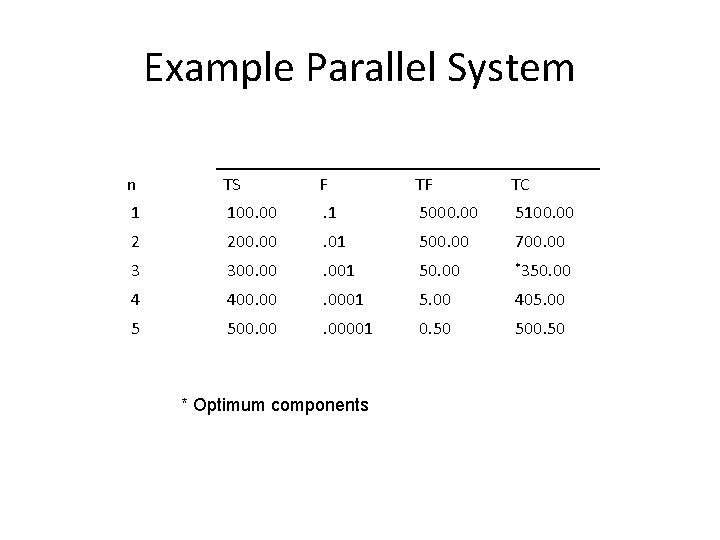
Example Parallel System n TS F TF TC 1 100. 00 . 1 5000. 00 5100. 00 2 200. 00 . 01 500. 00 700. 00 3 300. 001 50. 00 *350. 00 4 400. 0001 5. 00 405. 00 5 500. 00001 0. 50 500. 50 * Optimum components

Component Reliability • Factors affecting reliability – Temperature – Pressure – Age – Duty cycles

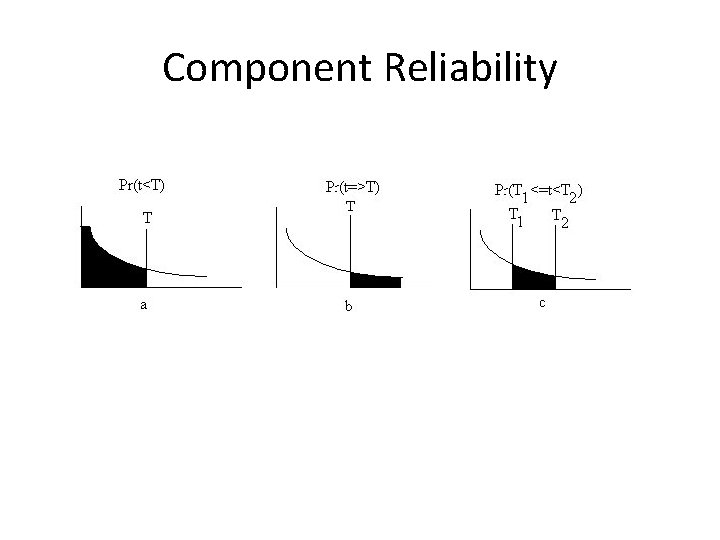
Component Reliability • Reliability has previously been defined as the probability that a system or component will operate in the next instant • r = 1 - Pr( Failure / T ) • Pr( Failure / T ) – Instantaneous Failure Rate (IFR) – Hazard Rate (HR).

Component Reliability • • Pr( Failure / T ) = { f(t) } / {Pr( t >= T ) } f(t) = failure probability density function f(t) = 1/m e-t/m (e = 2. 71828) m = Mean Time Before Failure (MTBF)
Component Reliability

Component Reliability

Component Reliability • r = 1 – Pr(Failure/T) • r = 1 – 1/m • r = a constant

Component Reliability Example • An LED display has a mean life of 100, 000 hours (100000/(365 *24))= 11. 5 years. • r = 1 – 1/100000 • r =. 99999

Component Reliability Example • What is the probability that an LED will last longer than 125, 000 hours in service? • Pr( t >= 125, 000 ) = e-125, 000/100, 000 = e-1. 25 =. 2865

Component Reliability Example • What is the probability that an LED will fail before its mean life? • Pr( t < 100, 000 ) = 1 - e-100, 000/100, 000 = 1 - e-1 =. 632

Weibul Probability Distribution • Pr( Failure / T ) = k * z-k * Tk - 1

Weibul • Exponential – k=1, z=m • Linear IFR –k=2
- Slides: 77