Reliability Prediction A Quest for Reliable Parameters By
Reliability Prediction A Quest for Reliable Parameters By Yair Shai 1

Goals • Compare the MTBCF & MTTCF parameters in view of complex systems engineering. • Failure repair policy as the backbone for realistic MTBCF calculation. • Motivation for modification of the technical specification requirements. 2

Promo : Description of Parameters t 1 t 2 t 3 t 4 Failure Event of an Item t 5 . . . . time r =Number of Failures = Se Mean Time Between Failures Non Repairable Items: Mean Time To Failure 3 m an t ic ? s Repairable Items: =
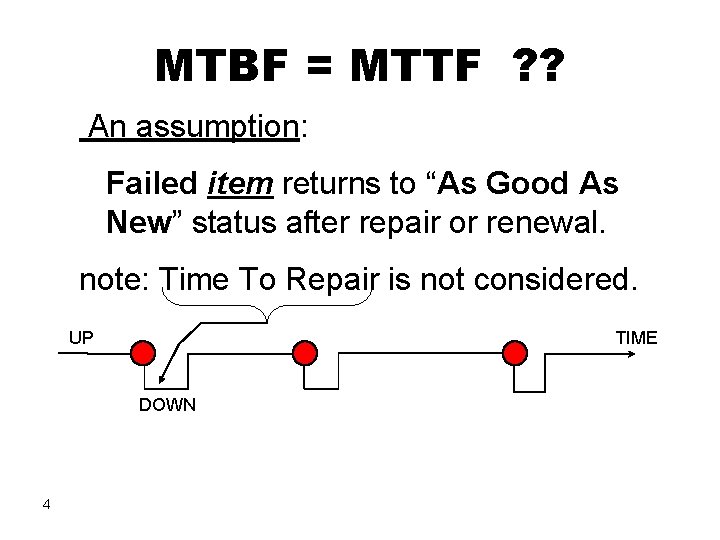
MTBF = MTTF ? ? An assumption: Failed item returns to “As Good As New” status after repair or renewal. note: Time To Repair is not considered. UP TIME DOWN 4
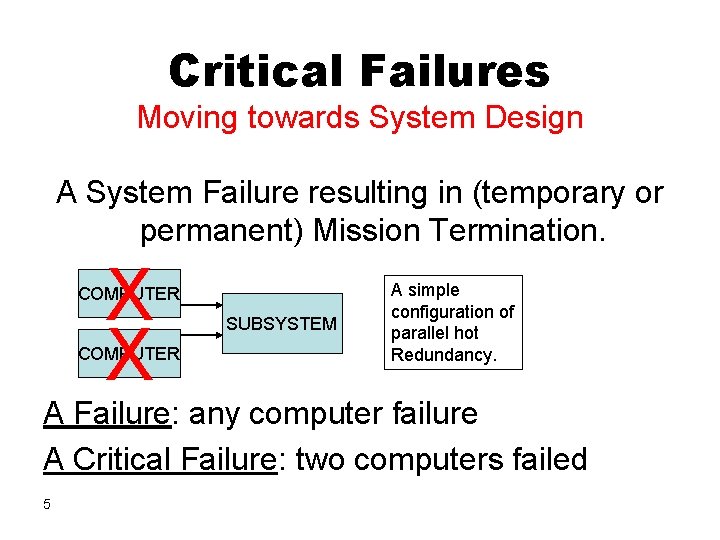
Critical Failures Moving towards System Design A System Failure resulting in (temporary or permanent) Mission Termination. X X COMPUTER SUBSYSTEM A simple configuration of parallel hot Redundancy. A Failure: any computer failure A Critical Failure: two computers failed 5

Critical Failures A clue for Design Architecture MTBCF Mean Time Between Critical Failures MTTCF Mean Time To Critical Failure SAME? Remember the assumptions Determining the failure repair policy: COLD REPAIR No time for repair actions during the mission 6
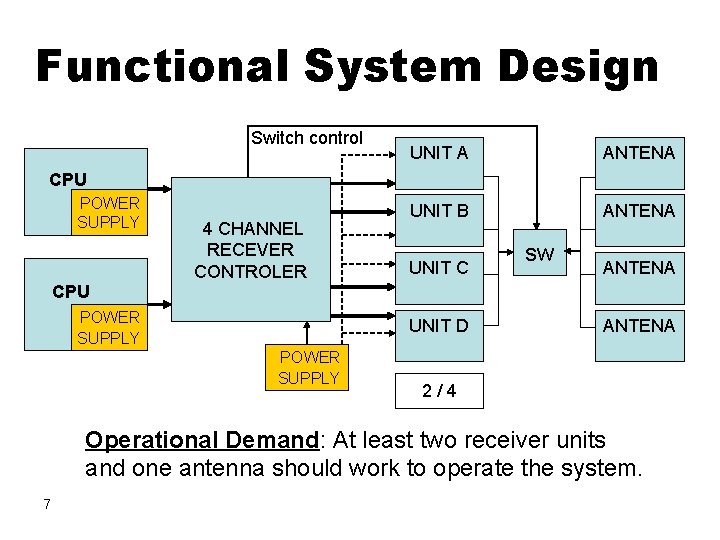
Functional System Design Switch control UNIT A ANTENA UNIT B ANTENA CPU POWER SUPPLY 4 CHANNEL RECEVER CONTROLER UNIT C sw ANTENA CPU POWER SUPPLY UNIT D POWER SUPPLY ANTENA 2/4 Operational Demand: At least two receiver units and one antenna should work to operate the system. 7
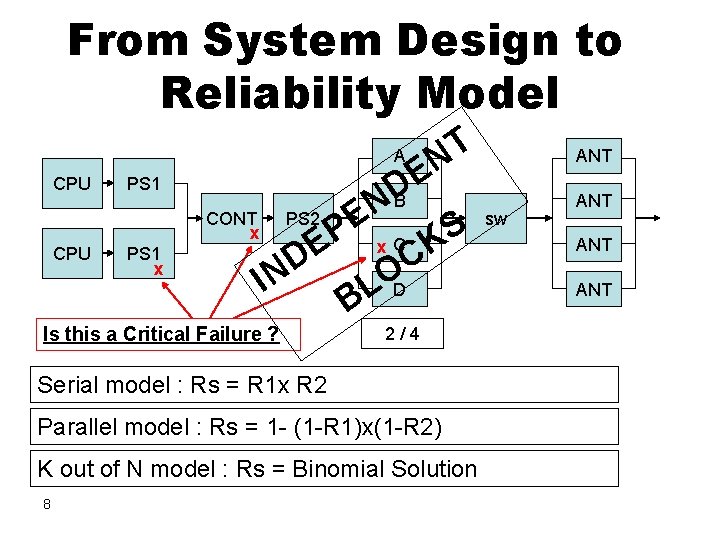
From System Design to Reliability Model A CPU CONT x CPU E D PS 1 x PS 2 D N I P E Is this a Critical Failure ? B N E x C T N S K C OD L B 2/4 Serial model : Rs = R 1 x R 2 Parallel model : Rs = 1 - (1 -R 1)x(1 -R 2) K out of N model : Rs = Binomial Solution 8 ANT sw ANT ANT

From RBD Logic Diagram to Reliability Function Simple mathematical manipulation: Rsys(t)= f( serial / parallel / K out of N) Classic parameter evaluation: WARNING !!! MTBCF MTTCF Is this realistic ? After[ each S. Zacks, repair Springer-Verlag of a critical failure 1991, -Introduction The whole system To returns Reliability to status Analysis, “As Good Par. As 3. 5] New”. 9

MTBCF vs. MTTCF A New Interpretation Common practice interpretation: First MTBCF = MTTCFF Each repair “Resets” the time count to idle status (or) Each failure is the first failure. Realistic interpretation: MTBCF = MTTCF Only failed Items which cause the failure are repaired to idle. All other components keep on aging. 10
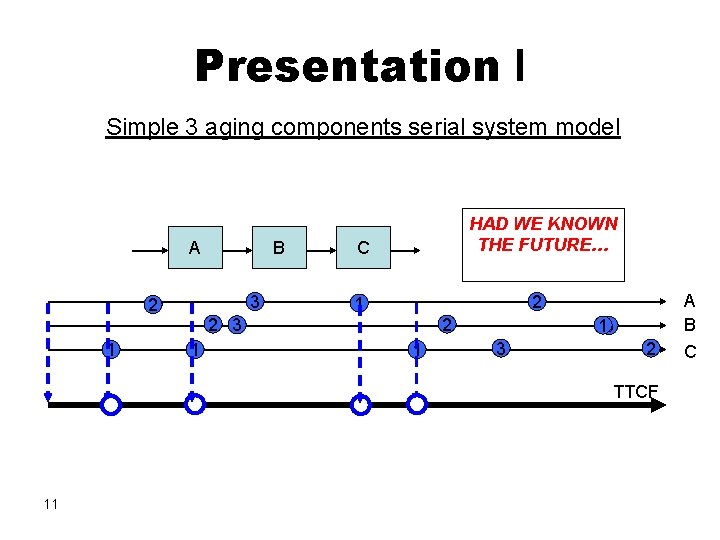
Presentation I Simple 3 aging components serial system model A 3 2 1 B HAD WE KNOWN THE FUTURE… C 2 1 2 3 1 2 1 13 3 2 TTCF 11 A B C
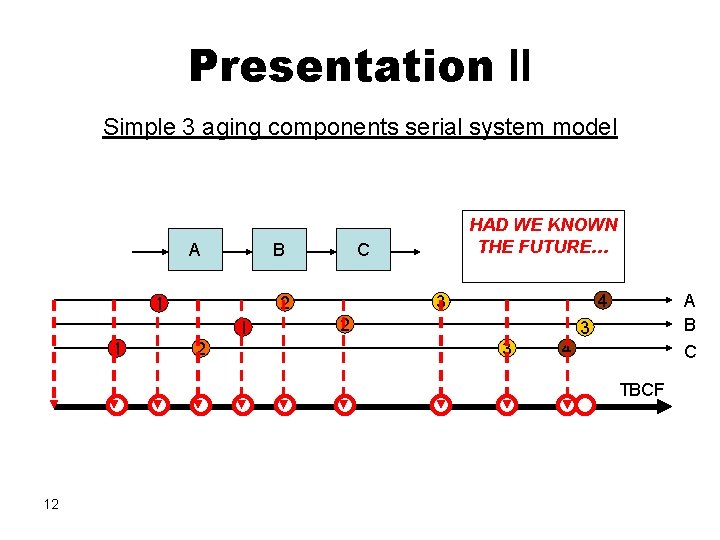
Presentation II Simple 3 aging components serial system model A B 1 1 C 2 4 3 2 1 HAD WE KNOWN THE FUTURE… 2 A B C 3 3 4 TBCF 12
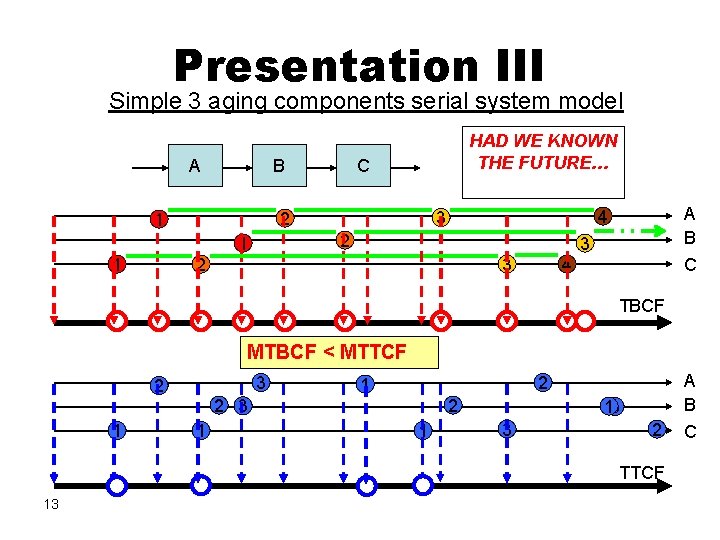
Presentation III Simple 3 aging components serial system model A B C 2 1 A B C 4 3 2 1 1 HAD WE KNOWN THE FUTURE… 3 2 3 4 TBCF MTBCF < MTTCF 3 2 1 2 3 1 2 1 13 3 2 TTCF 13 A B C
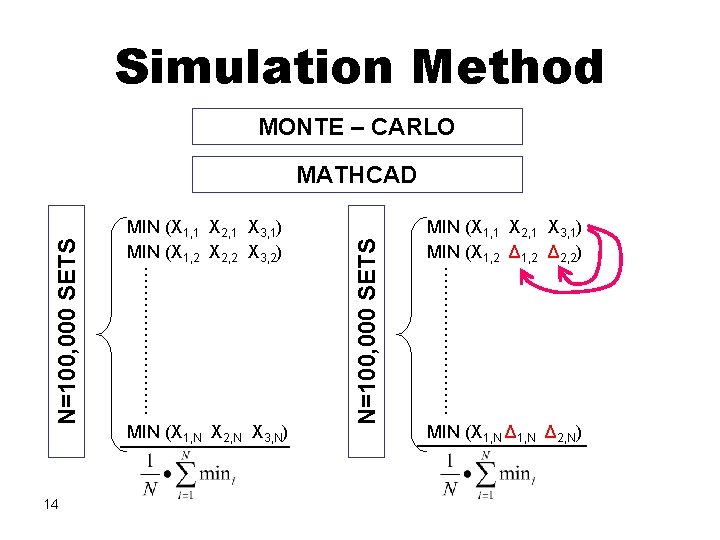
Simulation Method MONTE – CARLO 14 MIN (X 1, N X 2, N X 3, N) _________ MIN (X 1, 1 X 2, 1 X 3, 1) MIN (X 1, 2 Δ 2, 2) …………. N=100, 000 SETS MIN (X 1, 1 X 2, 1 X 3, 1) MIN (X 1, 2 X 2, 2 X 3, 2) …………. N=100, 000 SETS MATHCAD MIN (X 1, N Δ 2, N) _________

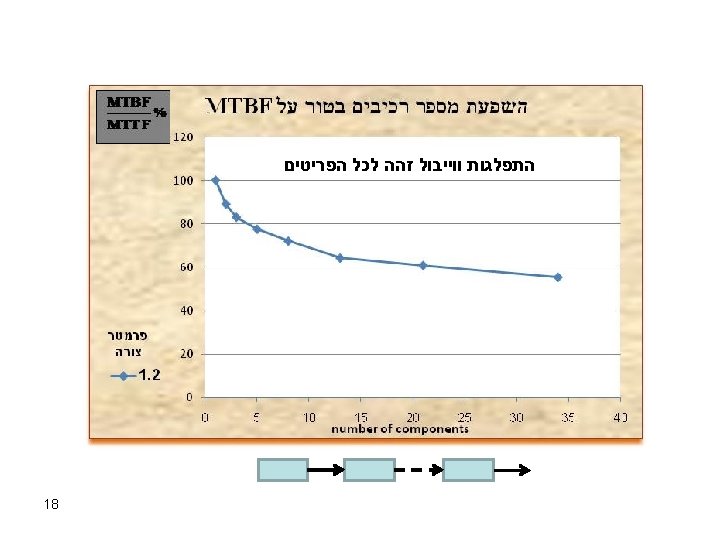
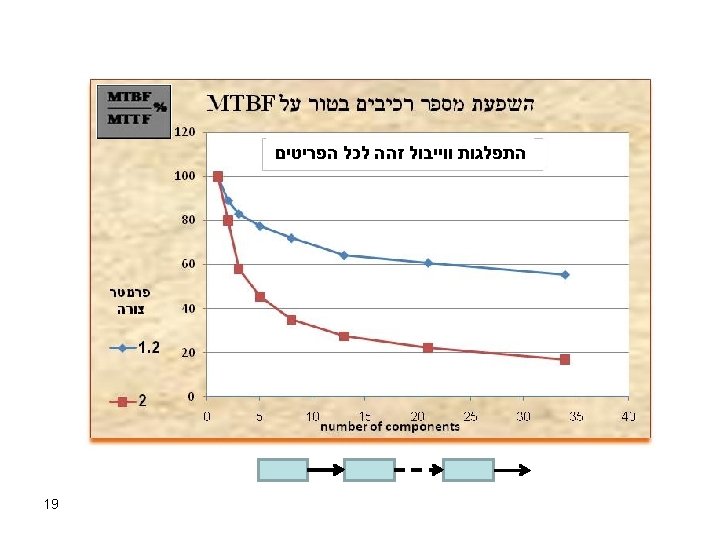
How “BIG” is the Difference ? 1. Depends on the System Architecture. 2. Depends on the Time-To-Failure distribution of each component. 3. The difference in a specific complex electronic system was found to be ~40% Note: True in redundant systems even when all components have constant failure rates. 15

Why Does It Matter ? Suppose a specification demand for a system’s reliability : MTBCF = 600 hour Suppose the manufacturer prediction of the parameter: X MTBCF = 780 hour -40% ATTENTION !!! How was it CALCULATED ? ? Is this MTBCF or MTTCF ? ? “Real” MTBCF = 480 < 600 (spec) 16
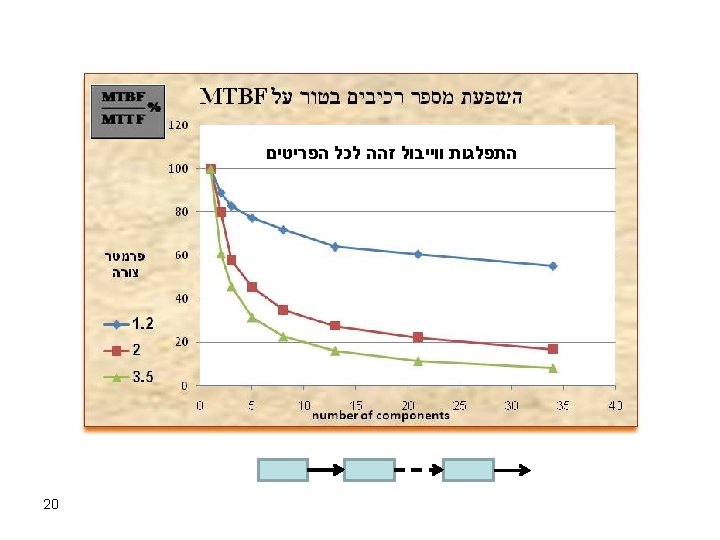
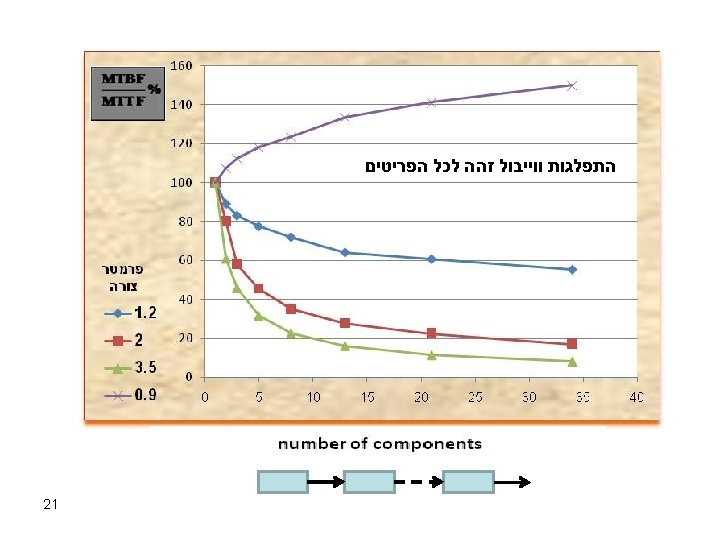
Example 1 Aging serial system – each component is weibull distributed 17
Example 2 Two redundant subsystems in series – each component is exponentially distributed 22
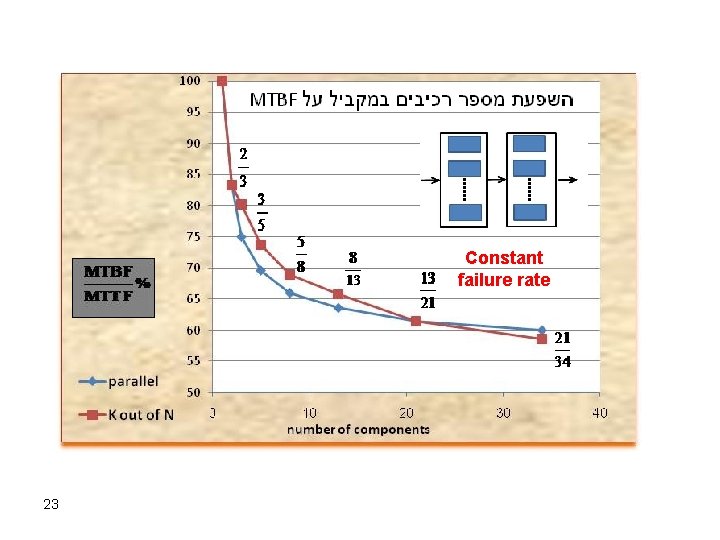
Constant failure rate 23
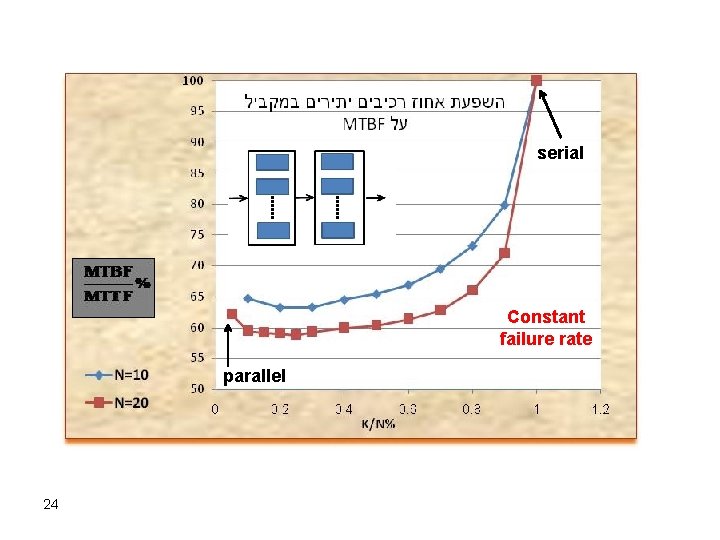
serial Constant failure rate parallel 24

A Comment about Asymptotic Availability (*) [ S. Zacks, Springer-Verlag 1991, Introduction To Reliability Analysis, Par 4. 3] 25

Repair policies 1. “Hot repair” is allowed for redundant components. 2. All components are renewed on every failure event. 3. All failed components are renewed on every failure event. 4. Failed components are renewed only in blocks which caused the system failure. 5. Failed subsystems are only partially renewed. 26

Conclusions • System configuration and distribution of components determine the gap. • Repair policy should be specified in advance to determine calculation method. • Flexible software solutions are needed to simulate real MTBCF for a given RBD. • Predict MTBCF not MTTCF 27
- Slides: 27