Reliability is an important function used to predict

Reliability is an important function used to predict the component’s of life time. It is not possible to predict when they will occur, it can cause the whole power systems to fail. When will the system fail and what will be the effect of the failure?

v Failures occur randomly, but we can make predictions about the future of systems by using methods involving probability and statistics. v Probability is used to express the reliability and availability of systems.

Tutorial – How the Component Fail…. . ? Briefly describe a condition that would result in each of the following components failing and when failed describe the likely effect on the component: i. Resistor …………. ? ii. Capacitor …………. . ? iii. Inductor/Transformer …………? iv. Diode…………………. . ? v. Switch or contact …………?

Reliability Function

Failure Function

Probability of Failure It is often useful to know the probability of failure during a small interval around time t. This can be found from the failure density function, f(t). The probability of failing, ΔQ(t), during a very small interval Δt at t can be expressed as : ΔQ(t) = f(t)Δt

The relationship between the failure density function, f(t), and the reliability function, R(t), and failure function, Q(t), is shown in figure. The integral form 0 to t is represented by the area under the curve of f(t) from o to t, giving Q(t). Similarly, R(t), is represented by the area under the curve of f(t) from t to infinity.

Hazard Rate

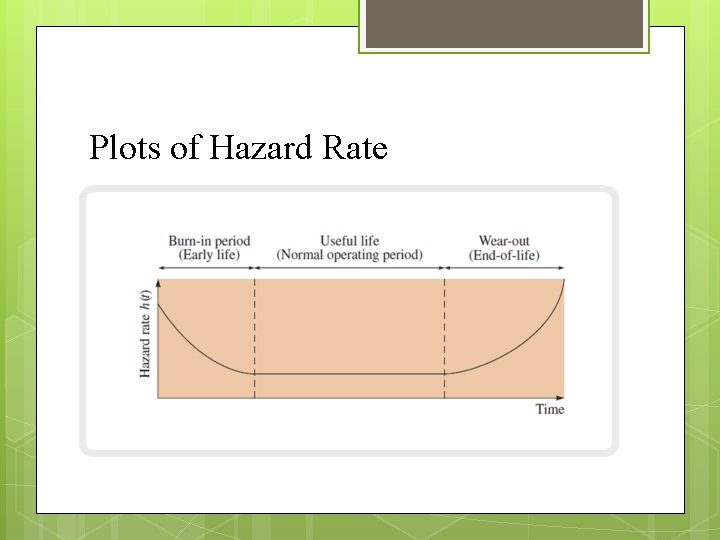
Plots of Hazard Rate

Average Lifetime

MTBF, MTTR and availability

R 1(t) R 2(t) Rn(t) The reliability of combinations of components or system elements an be represented by using reliability diagram, in Figure which components connected in series.

If a system fails only when all of its elements have failed then, in terms of reliability, the elements are in parallel. The failure function of two elements in parallel is therefore the product of the failure functions of the two components. So, the reliability function R(t) for the system is ; R(t) = 1 – Q 1(t)Q 2(t) = 1 -[1 -R 1(t)] [ 1 -R 2(t)] = R 1(t) + R 2(t) – R 1(t) R 2(t) R 1(t)

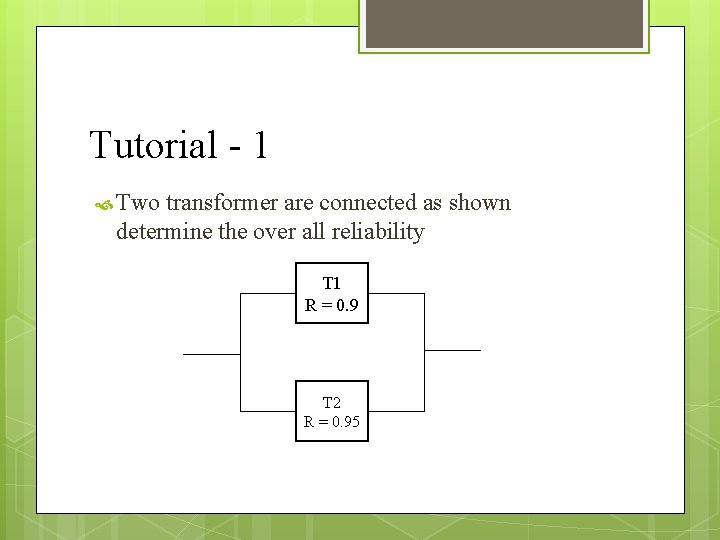
Tutorial - 1 Two transformer are connected as shown determine the over all reliability T 1 R = 0. 9 T 2 R = 0. 95

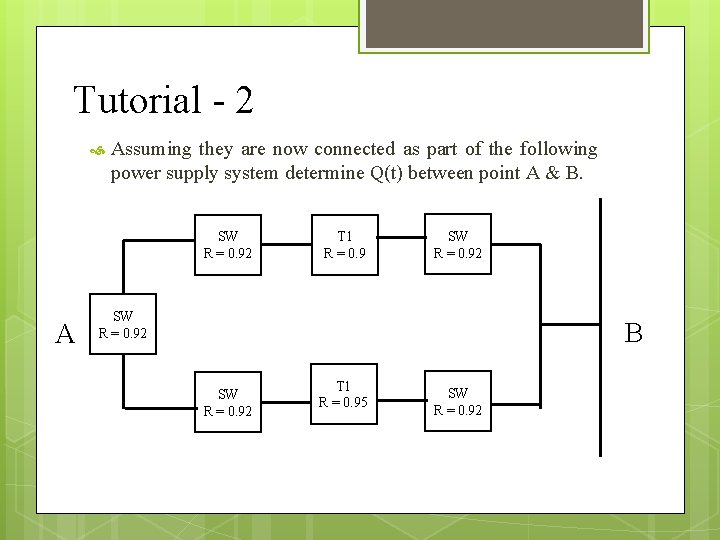
Tutorial - 2 Assuming they are now connected as part of the following power supply system determine Q(t) between point A & B. SW R = 0. 92 A T 1 R = 0. 9 SW R = 0. 92 B SW R = 0. 92 T 1 R = 0. 95 SW R = 0. 92