Reliability and Robustness in Engineering Design Zissimos P

Reliability and Robustness in Engineering Design Zissimos P. Mourelatos, Associate Prof. Jinghong Liang, Graduate Student Mechanical Engineering Department Oakland University Rochester, MI 48309, USA mourelat@oakland. edu 1

Outline § Definition of reliability-based design and robust design § Reliable / Robust design Ø Problem statement Ø Variability measure Ø Multi-objective optimization § Preference aggregation method Ø Indifferent designs § Examples § Summary and conclusions 2

Reliable Design Problem Statement Maximize Mean Performance subject to : Probabilistic satisfaction of performance targets Reliability 3

Robust Design Problem Statement Minimize Performance Variation subject to : Deterministic satisfaction of performance targets 4

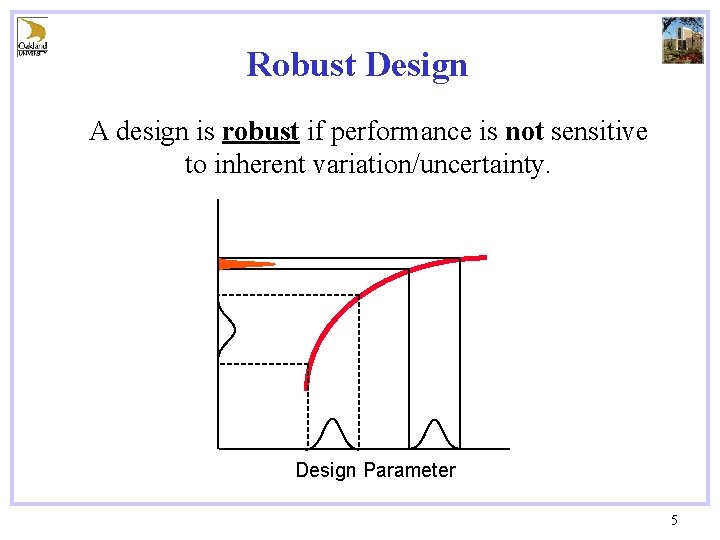
Robust Design A design is robust if performance is not sensitive to inherent variation/uncertainty. Design Parameter 5

Reliable & Robust Design under Uncertainty: Problem Statement Maximize Mean Performance Minimize Performance Variation Robustness subject to : Probabilistic satisfaction of performance targets Reliability 6

Reliable / Robust Design Problem Statement s. t. , Multi Objective where : : vector of deterministic design variables : vector of random design parameters 7

Reliable / Robust Design Problem: Issues § Variability Measure Calculation Ø Variance Ø Percentile Difference § Trade – offs in Multi – Objective Optimization Ø Preference Aggregation Method 8

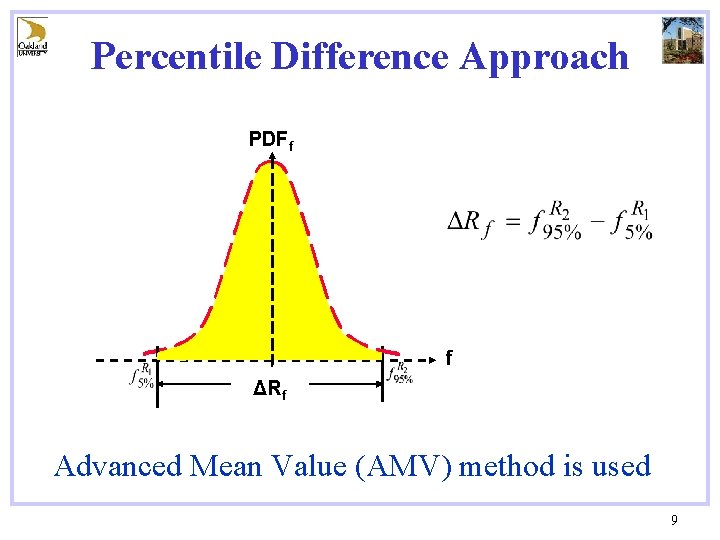
Percentile Difference Approach PDFf f ΔRf Advanced Mean Value (AMV) method is used 9

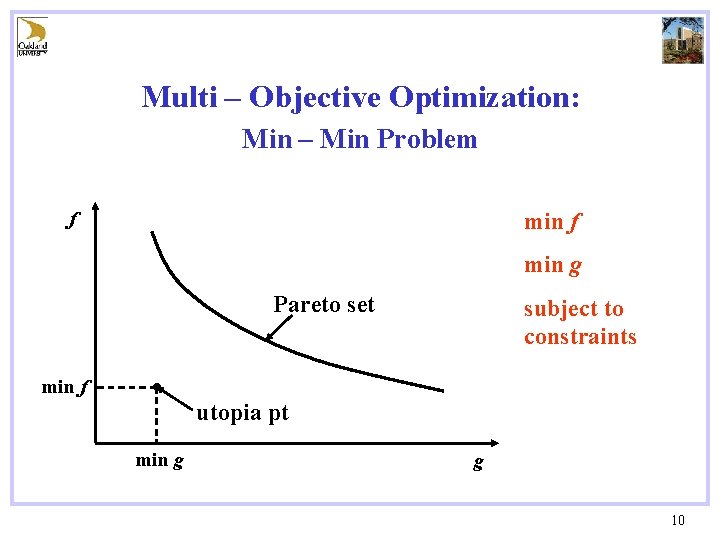
Multi – Objective Optimization: Min – Min Problem f min g Pareto set subject to constraints min f utopia pt min g g 10

Multi – Objective Optimization: Issues • Must calculate whole Pareto set Ø Series of RBDO problems Ø Visualize Pareto set Expensive • Choose “best” point on Pareto set (How? ? ) 11

Preference Aggregation Method • Capable of calculating whole Pareto set • Use of Indifferent Designs to only get the “best” point on Pareto set 12

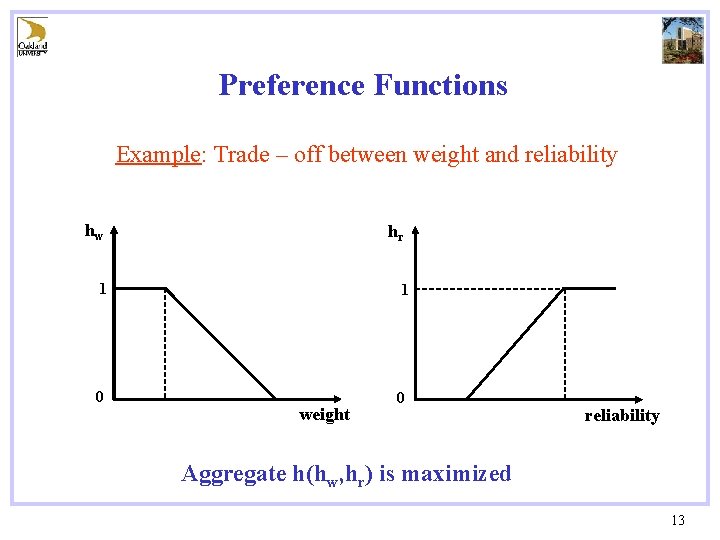
Preference Functions Example: Trade – off between weight and reliability hw hr 1 1 0 0 weight reliability Aggregate h(hw, hr) is maximized 13

Preference Aggregation Axioms Annihilation : Idempotency : Monotonicity : if Commutativity : Continuity : 14

Preference Aggregation Method satisfies annihilation for For only. Fully compensating : : Non - Compensating Aggregation is defined by 15

Preference Aggregation Properties • For any Pareto optimal point, there is always a set (s, w) to select it. • For any fixed s, there are Pareto sets for which some Pareto points can never be selected for any choice of w. 16

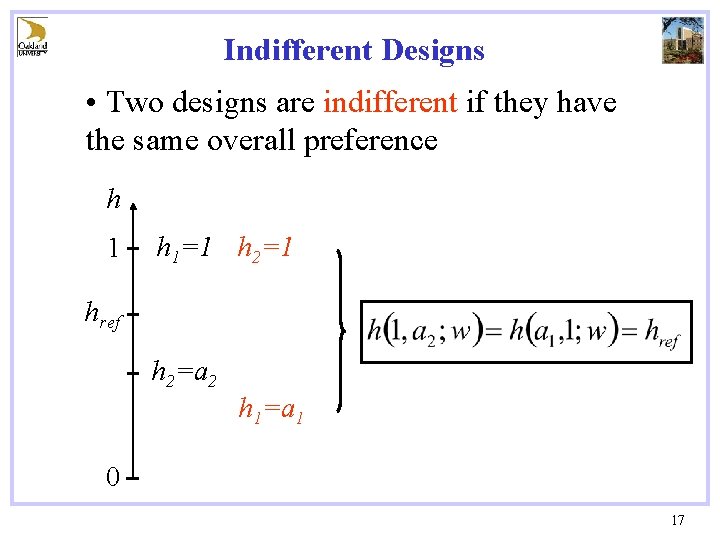
Indifferent Designs • Two designs are indifferent if they have the same overall preference h 1=1 h 2=1 href h 2=a 2 h 1=a 1 0 17

Indifferent Designs resulting in and The calculated (s, w) pair will select the “best” design on the Pareto set 18

A Mathematical Example s. t. Reliable/Robust Problem s. t. R = 99. 87% 19

A Mathematical Example RBDO Problem s. t. Robust Problem s. t. 20

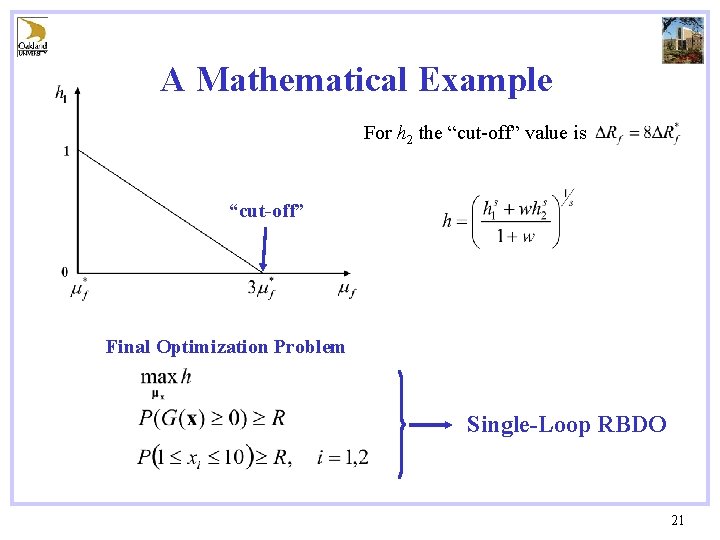
A Mathematical Example For h 2 the “cut-off” value is “cut-off” Final Optimization Problem Single-Loop RBDO 21

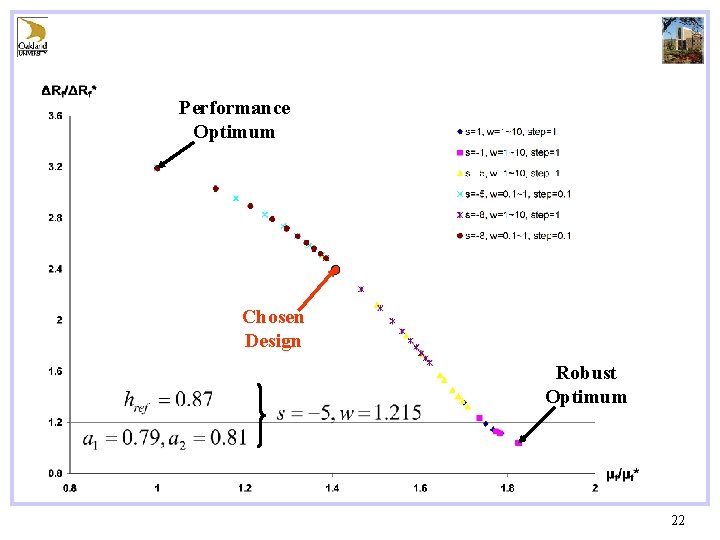
Performance Optimum Chosen Design Robust Optimum 22

A Mathematical Example Weighted Sum Approach s. t. . R=99. 87% 23

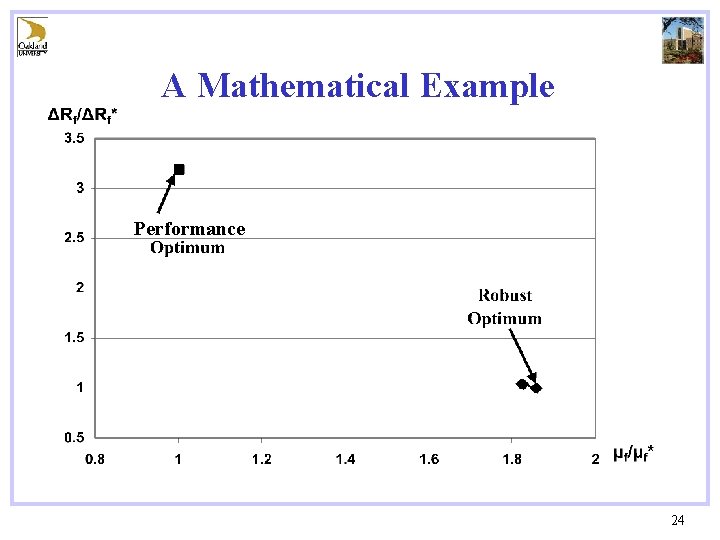
A Mathematical Example Performance 24

A Cantilever Beam Example Reliable/Robust Formulation • w, t : Normal R. V. ’s • y, E, Y, Z : Normal Random Parameters s. t. where: , • L : fixed • R = 99. 87% 25

A Cantilever Beam Example RBDO Problem s. t. , where: 26

A Cantilever Beam Example Robust Problem s. t. , where: 27

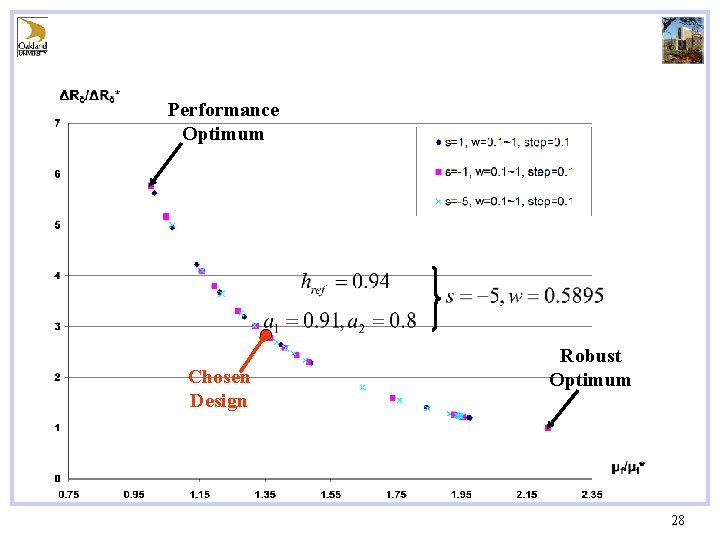
Performance Optimum Chosen Design Robust Optimum 28

Summary and Conclusions § A methodology was presented for trading-off performance and robustness § A multi – objective optimization formulation was used Ø Preference aggregation method handles trade – offs Ø Variation is reduced by minimizing a percentile difference Ø AMV method is used to calculate percentiles Ø A single – loop probabilistic optimization algorithm identifies the reliable / robust design § Examples demonstrated the feasibility of the proposed method 29

Q&A 30

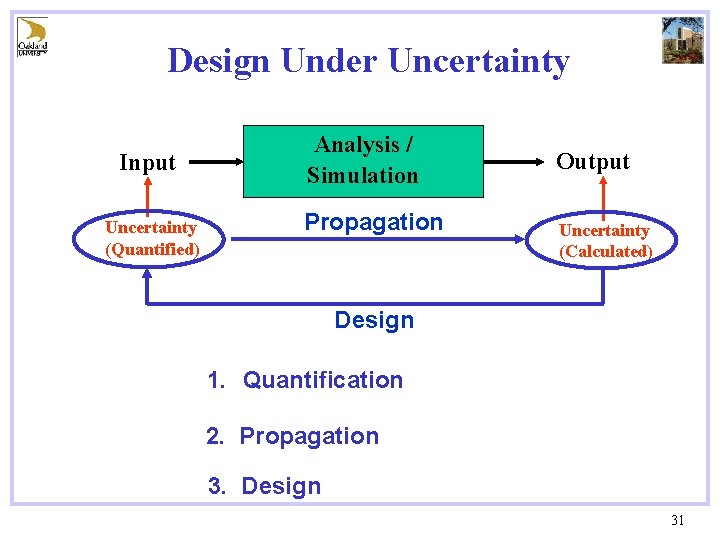
Design Under Uncertainty Input Uncertainty (Quantified) Analysis / Simulation Propagation Output Uncertainty (Calculated) Design 1. Quantification 2. Propagation 3. Design 31

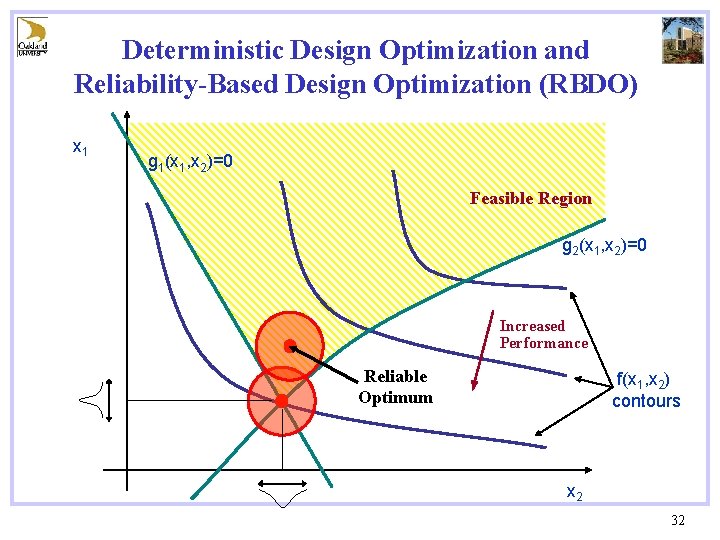
Deterministic Design Optimization and Reliability-Based Design Optimization (RBDO) x 1 g 1(x 1, x 2)=0 Feasible Region g 2(x 1, x 2)=0 Increased Performance Reliable Optimum f(x 1, x 2) contours x 2 32

RBDO Problem Statement s. t. , Single Objective where : : vector of deterministic design variables : vector of random design parameters 33

Indifferent Designs • Two designs are indifferent if they have the same overall preference • Designer provides specific preferences a 1=h 1(xi) and a 2=h 2(xi) so that : 34