RELAZIONI TRA 2 FENOMENI QUANTITATIVI Es 6 famiglie










































































- Slides: 99

RELAZIONI TRA 2 FENOMENI QUANTITATIVI

Es: 6 famiglie, ammontare della spesa annua (in euro) per l’acquisto di due generi di largo consumo: latte fresco e biscotti. Famiglia Spesa annua per l’acquisto di latte fresco (€) Spesa annua per l’acquisto di biscotti (€) A 105 65 B 190 130 C 80 160 D 120 90 E 240 220 F 60 50 M(x)= 132. 5 M(y)= 119. 2 • (i) rxy? (ii) commento (iii) diagramma di dispersione (iv) concordanza tra rxy e diagramma di dispersione (v) Perché rxy invece della retta di regressione?

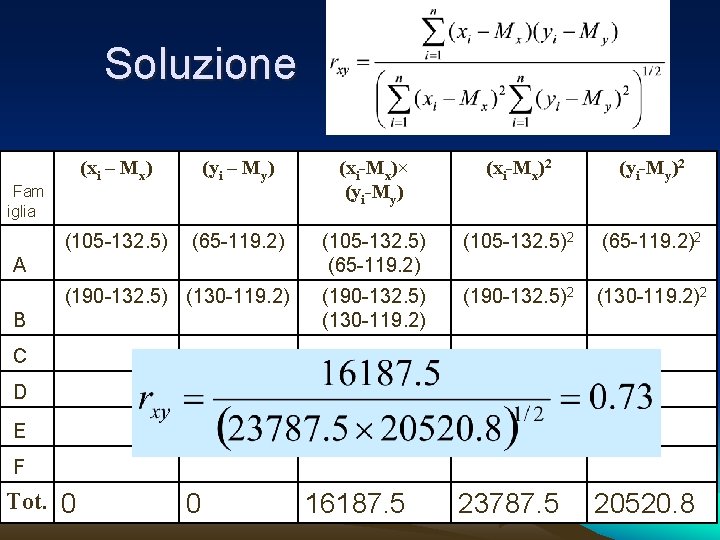
Soluzione (xi – Mx) (yi – My) (xi-Mx)× (yi-My) (xi-Mx)2 (yi-My)2 (105 -132. 5) (65 -119. 2) (105 -132. 5)2 (65 -119. 2)2 (190 -132. 5) (130 -119. 2) (190 -132. 5)2 (130 -119. 2)2 23787. 5 20520. 8 Fam iglia A B C D E F Tot. 0 0 16187. 5

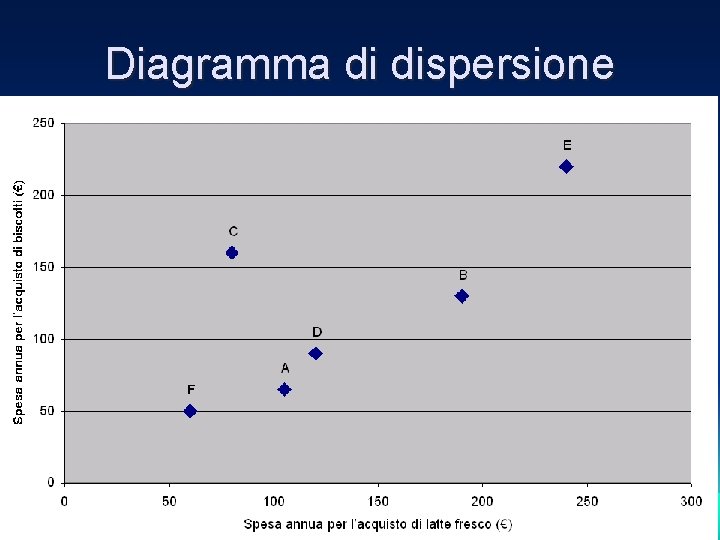
Diagramma di dispersione

Diagramma di dispersione in termini di scostamenti dalla media

Analisi del diagramma di dispersione • Il punto C è un valore anomalo bivariato • Se cancelliamo il punto C ci attendiamo che il valore di rxy aumenti • rxy senza il punto C è uguale a 0. 963

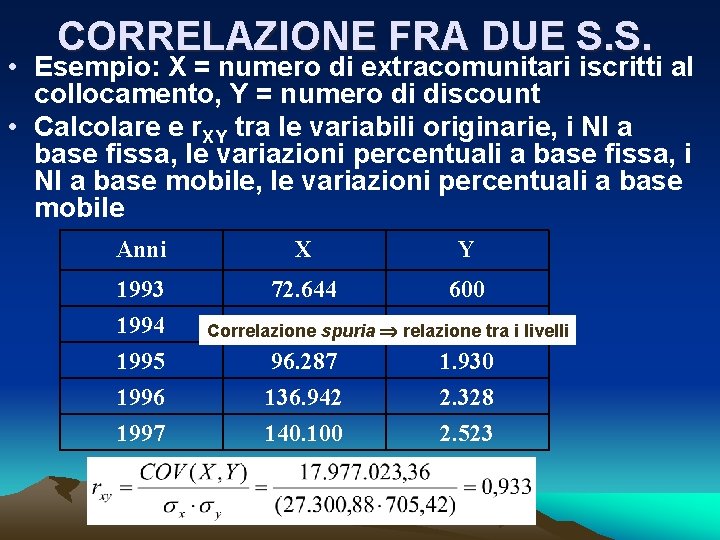
CORRELAZIONE FRA DUE S. S. • Esempio: X = numero di extracomunitari iscritti al collocamento, Y = numero di discount • Calcolare e commentare r. XY tra le variabili originarie, i NI a base fissa, le variazioni percentuali a base fissa, i NI a base mobile, le variazioni percentuali a base mobile Anni X Y 1993 1994 1995 72. 644 85. 993 96. 287 600 1. 300 1. 930 1996 1997 136. 942 140. 100 2. 328 2. 523

CORRELAZIONE FRA DUE S. S. • Esempio: X = numero di extracomunitari iscritti al collocamento, Y = numero di discount • Calcolare e r. XY tra le variabili originarie, i NI a base fissa, le variazioni percentuali a base fissa, i NI a base mobile, le variazioni percentuali a base mobile Anni 1993 1994 1995 1996 1997 X Y 72. 644 600 85. 993 1. 300 tra i livelli Correlazione spuria relazione 96. 287 1. 930 136. 942 140. 100 2. 328 2. 523

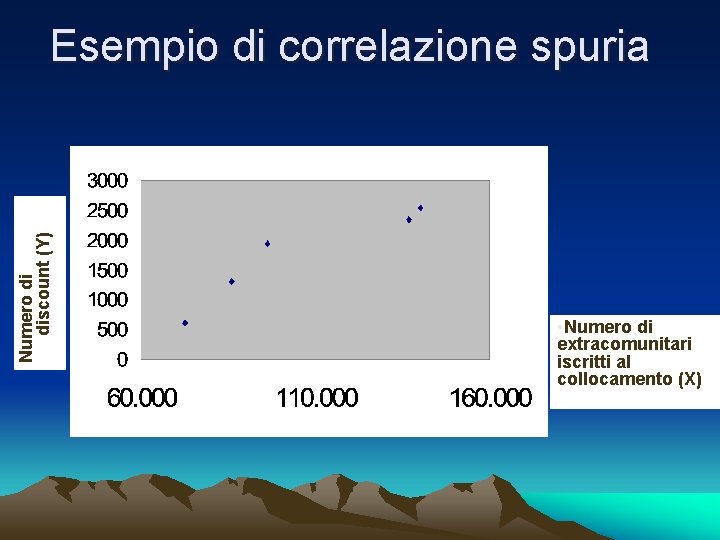
Numero di discount (Y) Esempio di correlazione spuria • Numero di extracomunitari iscritti al collocamento (X)

Numero di discount (Y) Esempio di correlazione spuria • Numero di extracomunitari iscritti al collocamento (X) • Correlazione tra le variazioni annue?

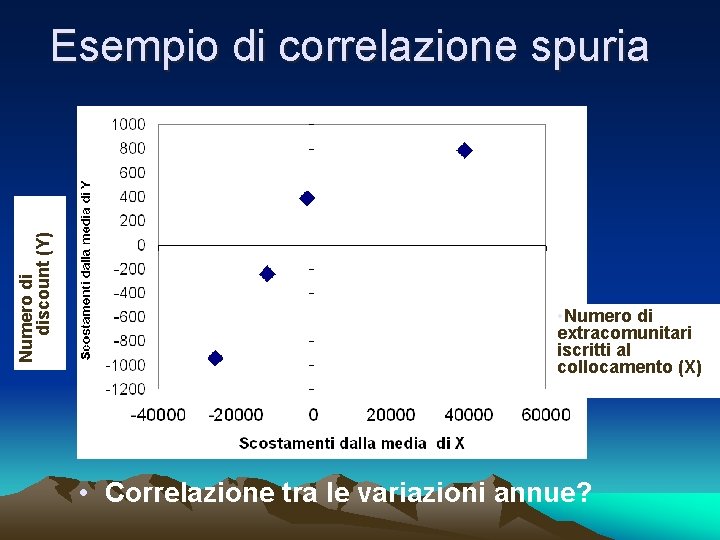
Esempio di correlazione spuria • Numero di extracomunitari iscritti al collocamento (X) • Numero di discount (Y) • Correlazione tra le variazioni annue?

NI base mobile X (numero di extracomunitari) e Y (numero di discount Var % X Var % Y Scost media X 216, 67 18, 38 116, 67 -0, 34 68, 14 111, 97 148, 46 11, 97 48, 46 -6, 75 -0, 07 1996 142, 22 120, 62 42, 22 20, 62 23, 50 -27, 91 1997 102, 31 108, 38 2, 31 8, 38 -16, 41 -40, 16 Media 118, 72 148, 53 18, 72 Var 0, 0217 0, 1758 Anni n. i. base mobile 1993 - - 1994 118, 38 1995 48, 53 0, 00 Scost media Y 0, 00 Cov(Nix, NIy)=0, 000496 rxy(tra n. i. a base mobile) =-0, 000496/(0, 0217*0, 1758)½ = -0, 008

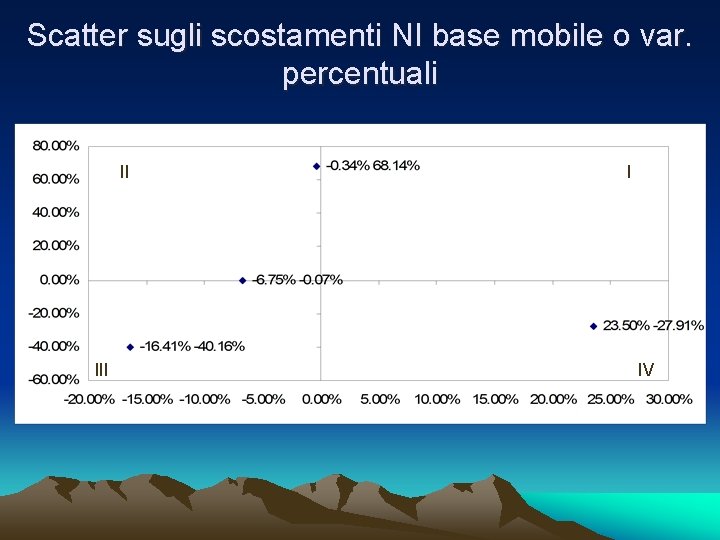
Scatter sugli scostamenti NI base mobile o var. percentuali II I IV

Osservazioni finali • Non esiste relazione lineare tra le variazioni annue di X e Y • Si ottiene rxy = -0, 008 anche effettuando il calcolo sulle variazioni % rispetto all’anno precedente (proprietà di invarianza per trasformazioni lineari crescenti)

Cenni alle analisi multivariate • p fenomeni quantitativi • Possiamo calcolare il coefficiente di correlazione lineare e/o la covarianza per ogni coppia di fenomeni

MATRICE DI COVARIANZA (p. 169) • p variabili: X 1, X 2, X 3, …, Xs, …, Xp

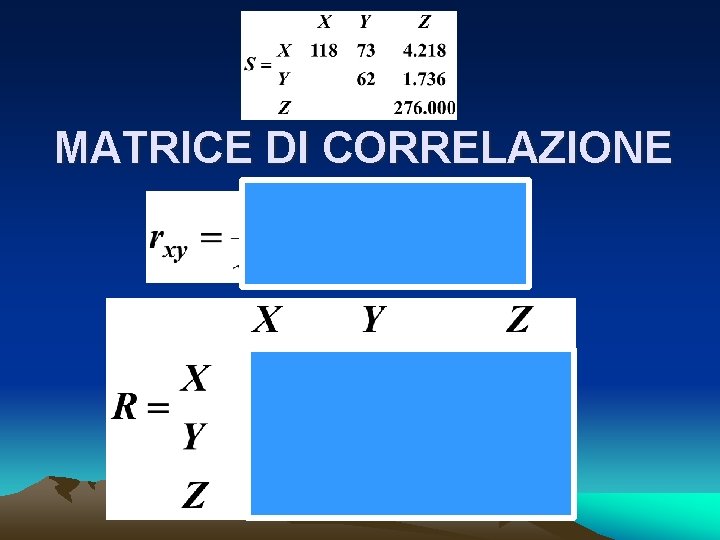
MATRICE DI CORRELAZIONE

ESEMPIO MATRICE DI COVARIANZA • X = età • Y = anzianità di servizio • Z = stipendio mensile (in euro)

MATRICE DI CORRELAZIONE

La diapositiva che segue contiene un esercizio da risolvere

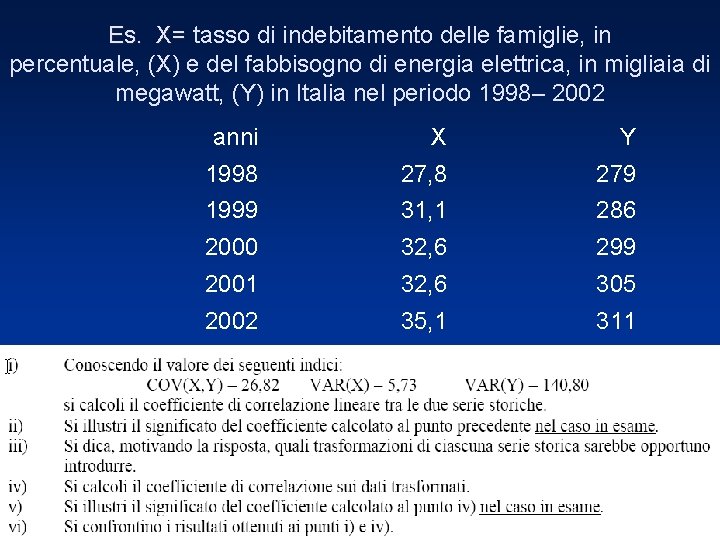
Es. X= tasso di indebitamento delle famiglie, in Es. X= percentuale, (X) e del fabbisogno di energia elettrica, in migliaia di megawatt, (Y) in Italia nel periodo 1998– 2002 anni X Y 1998 27, 8 279 1999 31, 1 286 2000 32, 6 299 2001 32, 6 305 2002 35, 1 311

LA REGRESSIONE LINEARE

LA REGRESSIONE LINEARE • • • Esiste una relazione (lineare) tra X e Y? In caso affermativo: Come varia una variabile (dipendente) in funzione dell’altra (esplicativa)? • Per convenzione: Y = variabile dipendente X = variabile esplicativa

Esempi • Relazione tra comportamenti di acquisto e caratteristiche dei consumatori • Relazione tra numero di esami sostenuti nei primi due anni di corso e voto alla maturità • Relazione tra prezzo di vendita e quantità venduta di un bene

Motivi che spingono ad adottare modelli di regressione lineare • Semplicità facilità di interpretazione dei parametri • yi = a + bxi + ei i = 1, …, n dove: • a + bxi rappresenta una retta: • a = ordinata all’origine intercetta • b = coeff. angolare coeff. di regressione • ei è un termine di errore (accidentale)

Motivi che spingono ad adottare modelli di regressione lineare • Effettiva linearità molte relazioni sono molto vicine alla linearità • Trasformazioni la relazione è lineare dopo aver trasformato opportunamente la dipendente e/o l’esplicativa • Es. y = a bx • log y = log a + (log b) x • y’ = a’ + b’ x

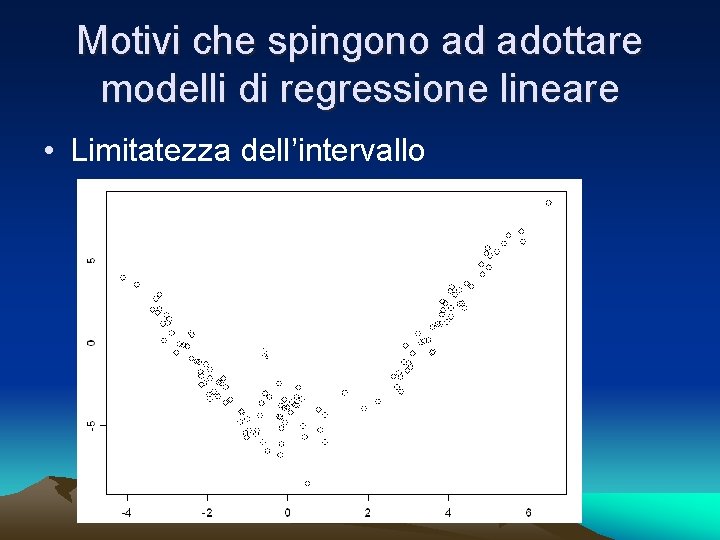
Motivi che spingono ad adottare modelli di regressione lineare • Limitatezza dell’intervallo

Motivi che spingono ad adottare modelli di regressione lineare • Ragioni di teoria statistica: lo studio delle funzioni lineari nei parametri ha una trattazione più agevole

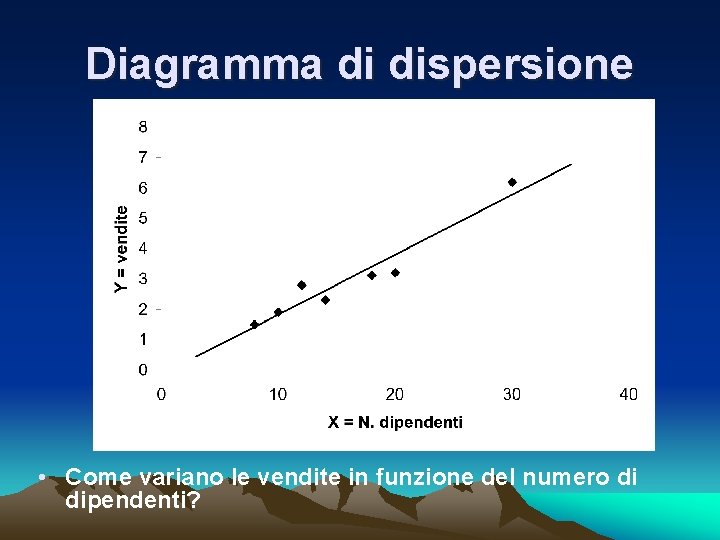
Diagramma di dispersione • Come variano le vendite in funzione del numero di dipendenti?

MODELLO DI REGRESSIONE • yi = a + bxi + ei i = 1, …, n dove: • a + bxi rappresenta una retta: • a = ordinata all’origine intercetta • b = coeff. angolare coeff. di regressione • ei è un termine di errore (accidentale)

RETTA DI REGRESSIONE • i = 1, …, n = valore teorico (valore stimato) di yi funzione lineare di i = 1, …, n Residui

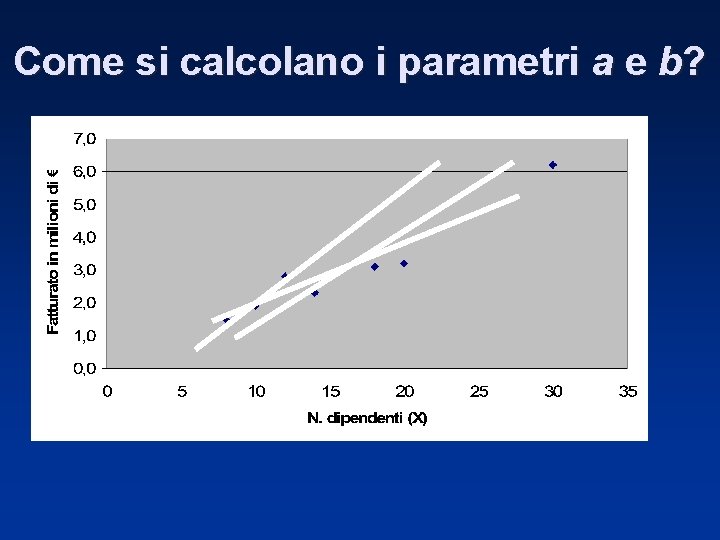
Come si calcolano i parametri a e b?

Come si calcolano i parametri a e b? • METODO DEI MINIMI QUADRATI Le incognite sono i parametri della retta

Visualizzazione grafica dei residui (e i )

Come si calcolano i parametri a e b? • METODO DEI MINIMI QUADRATI

Come si calcolano i parametri a e b? • METODO DEI MINIMI QUADRATI

Come si calcolano i parametri a e b? • METODO DEI MINIMI QUADRATI

Sistema di equazioni normali 2 equazioni e 2 incognite (a e b)

Dalla prima equazione

Sostituendo il valore trovato di a nella seconda equazione

Espressioni alternative per a e b

ESEMPIO (7 supermercati) rxy=0, 96 A B C D E F G Me die N. dipendenti (X) 10 18 Fatturato in milioni di € (Y) 1, 9 3, 1 20 8 30 12 14 16 3, 2 1, 5 6, 2 2, 8 2, 3 3

Calcolo di a e b xi yi xi 2 yi 2 xiyi A 10 1, 9 100 3, 61 19 B 18 3, 1 324 9, 61 55, 8 C 20 3, 2 400 10, 24 64 D 8 1, 5 E 30 6, 2 F 12 2, 8 G 14 2, 3 Tot. 112 21 2128 77, 28 402, 6

Calcolo di a e b xi yi xi 2 yi 2 xiyi A 10 1, 9 100 3, 61 19 B 18 3, 1 324 9, 61 55, 8 C 20 3, 2 400 10, 24 64 D 8 1, 5 E 30 6, 2 F 12 2, 8 G 14 2, 3 Tot. 112 21 2128 77, 28 402, 6

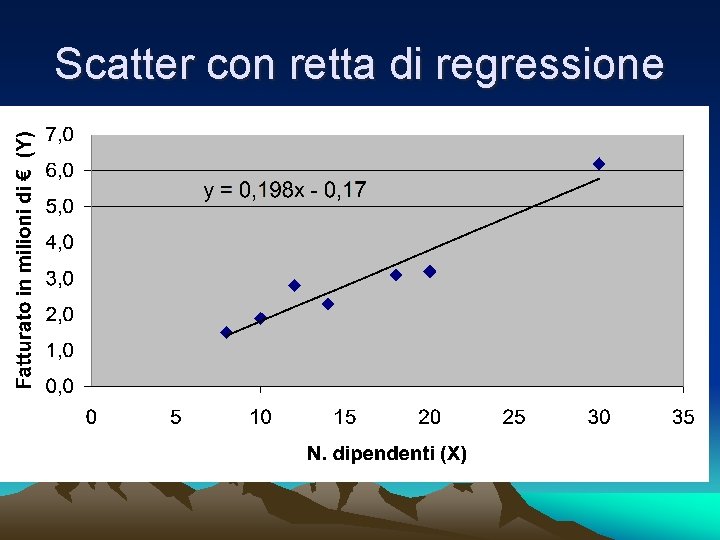
Scatter con retta di regressione

Interpretazione dei parametri ESEMPIO (7 supermercati) • a = – 0, 17 fatturato teorico quando N. di dipendenti = 0 • b = 0, 198 incremento medio nel fatturato quando il numero di dipendenti aumenta di 1 unità

Interpretazione di b • b= indica l’entità della variazione teorica della variabile dipendente in corrispondenza di un incremento unitario della variabile esplicativa

Interpretazione di b • a+bx • a+b(x+1) • Qual è la differenza tra i due precedenti valori teorici(prima e dopo l’incremento unitario)? • a+b(x+1)-(a+bx)=b

Sistema di equazioni normali Analizziamo le implicazioni dei due precedenti vincoli

Proprietà delle stime dei minimi quadrati • Proprietà 1: • Proprietà 2 • La retta di regressione passa sempre per il punto di coordinate

Proprietà delle stime dei minimi quadrati • Proprietà 3:

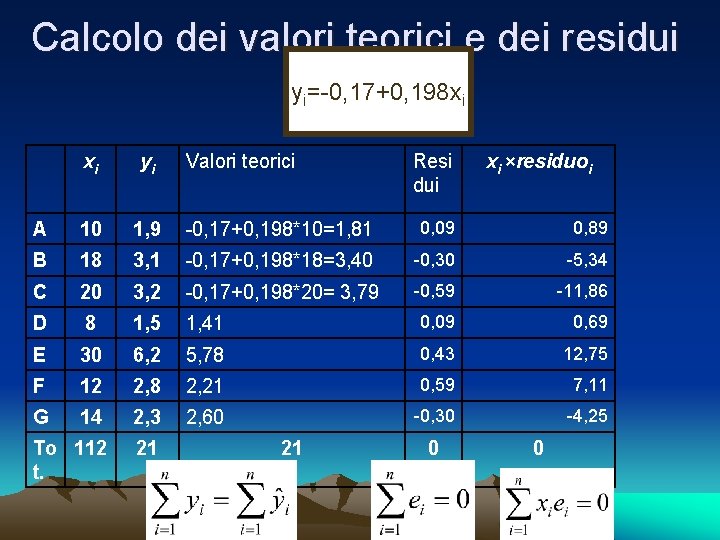
Calcolo dei valori teorici e dei residui yi=-0, 17+0, 198 xi xi yi Valori teorici A 10 1, 9 -0, 17+0, 198*10=1, 81 0, 09 0, 89 B 18 3, 1 -0, 17+0, 198*18=3, 40 -0, 30 -5, 34 C 20 3, 2 -0, 17+0, 198*20= 3, 79 -0, 59 -11, 86 D 8 1, 5 1, 41 0, 09 0, 69 E 30 6, 2 5, 78 0, 43 12, 75 F 12 2, 8 2, 21 0, 59 7, 11 G 14 2, 3 2, 60 -0, 30 -4, 25 To 112 t. 21 21 Resi dui 0 xi ×residuoi 0

Regressione in termini di scostamenti Dato che la sommatoria degli scostamenti dalla media è zero • Si ottiene che a=0

Modi alternativi di esprimere b • Dato che • Si ricava

ESEMPIO (7 supermercati):

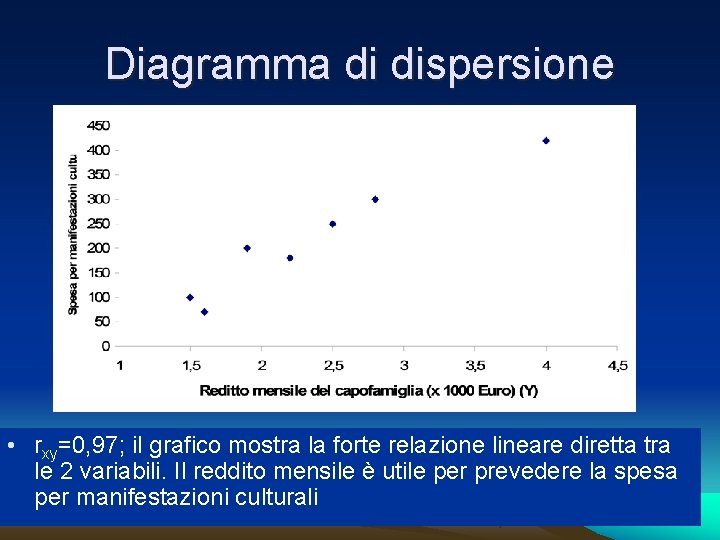
Es. n. 5. 7 famiglie A B C D E F G Spesa per manifestazion i culturali (Z) 200 420 250 70 180 300 100 Reddito mensile del capofamiglia (x 1000 Euro) (Y) 1, 9 4, 0 2, 5 1, 6 2, 2 2, 8 1, 5 • Costruire il diagramma di dispersione • Calcolare e commentare r. YZ • Sulla base dei risultati ottenuti si dica se è ragionevole adattare una retta di regressione; in questo caso quale sarebbe la dipendente e quale sarebbe l’esplicativa?

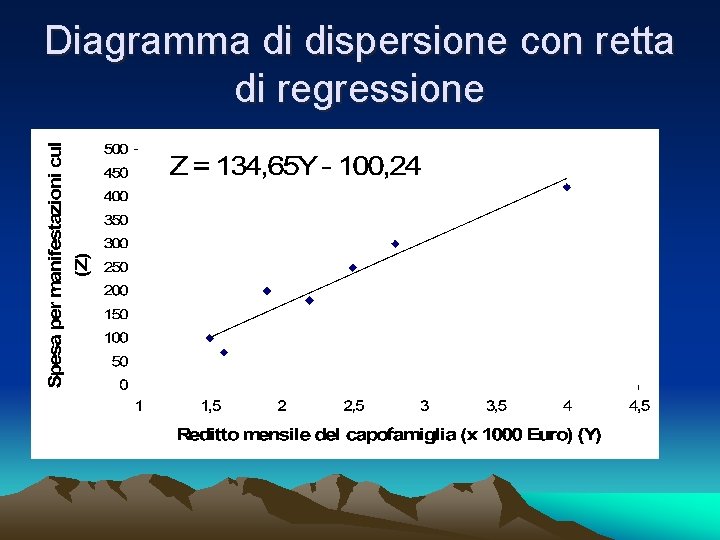
Diagramma di dispersione • rxy=0, 97; il grafico mostra la forte relazione lineare diretta tra le 2 variabili. Il reddito mensile è utile per prevedere la spesa per manifestazioni culturali

Diagramma di dispersione con retta di regressione

Scomposizione di yi

BONTA’ DI ADATTAMENTO • Occorre analizzare i residui DEVIANZA RESIDUA • L’adattamento è buono quando DEV(E) è “piccola” • Problemi: • DEV(E) cresce all’aumentare del numero di osservazioni (n) • DEV(E) dipende dall’unità di misura e dall’ordine di grandezza di Y

In qualsiasi modello di regressione con o senza intercetta è valida la relazione che segue • Questa relazione sfrutta la terza proprietà delle stime dei minimi quadrati (vincolo della derivata parziale rispetto a b posta uguale a 0)

Dimostrazione L’ultimo termine è zero dato che

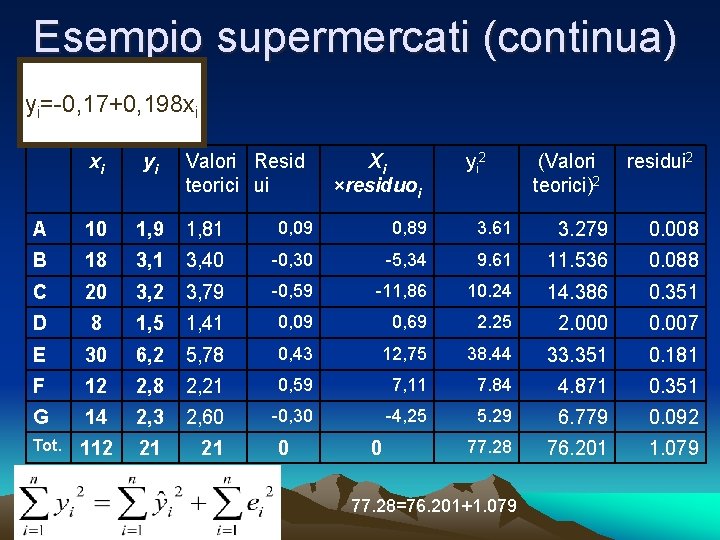
Esempio supermercati (continua) yi=-0, 17+0, 198 xi xi yi A 10 1, 9 1, 81 0, 09 0, 89 3. 61 3. 279 0. 008 B 18 3, 1 3, 40 -0, 30 -5, 34 9. 61 11. 536 0. 088 C 20 3, 2 3, 79 -0, 59 -11, 86 10. 24 14. 386 0. 351 D 8 1, 5 1, 41 0, 09 0, 69 2. 25 2. 000 0. 007 E 30 6, 2 5, 78 0, 43 12, 75 38. 44 33. 351 0. 181 F 12 2, 8 2, 21 0, 59 7, 11 7. 84 4. 871 0. 351 G 14 2, 3 2, 60 -0, 30 -4, 25 5. 29 6. 779 0. 092 112 21 21 77. 28 76. 201 1. 079 Tot. Valori Resid teorici ui 0 Xi ×residuoi 0 yi 2 77. 28=76. 201+1. 079 (Valori teorici)2 residui 2

Indice di bontà di adattamento nei modelli di regressione senza intercetta Varia nell’intervallo [0 1]

BONTA’ DI ADATTAMENTO • Retta di regressione: DEVIANZA TOTALE DEVIANZA DI REGRESSIONE DEVIANZA RESIDUA

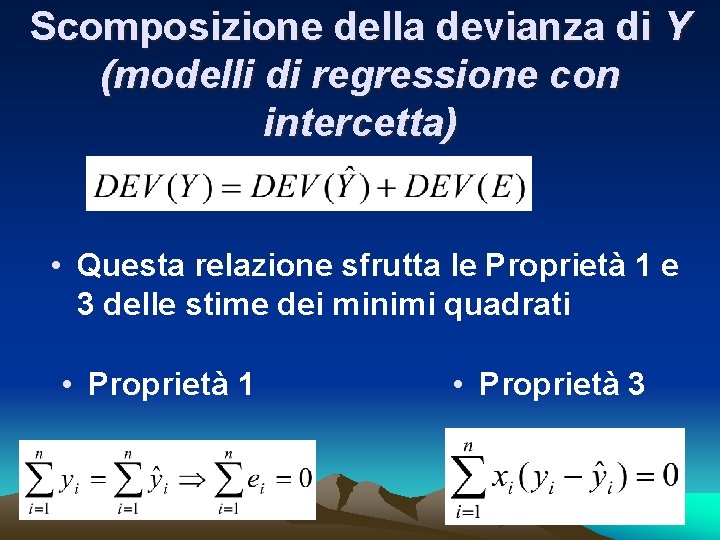
Scomposizione della devianza di Y (modelli di regressione con intercetta) • Questa relazione sfrutta le Proprietà 1 e 3 delle stime dei minimi quadrati • Proprietà 1 • Proprietà 3

Dimostrazione

Indice di determinazione lineare (R 2) • =1 se • =0 se

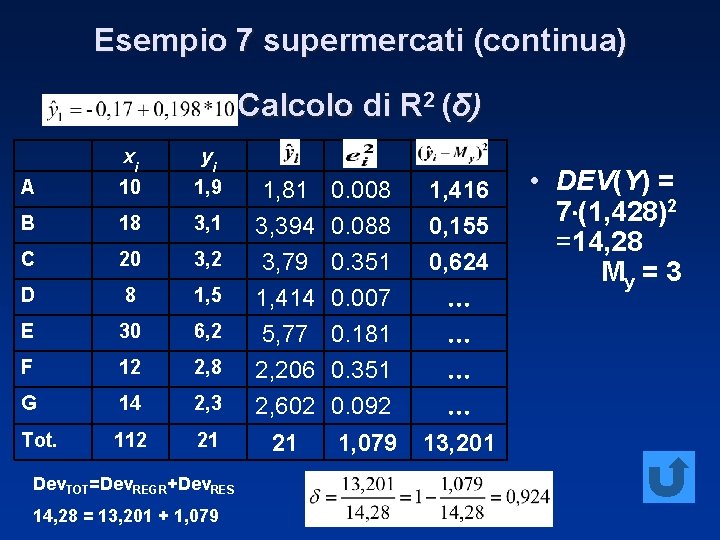
Esempio 7 supermercati (continua) Calcolo di R 2 (δ) xi yi A 10 1, 9 B 18 3, 1 C 20 3, 2 D 8 1, 5 E 30 6, 2 F 12 2, 8 G 14 Tot. 112 0. 008 0. 088 0. 351 0. 007 0. 181 0. 351 0. 092 1, 416 0, 155 0, 624 2, 3 1, 81 3, 394 3, 79 1, 414 5, 77 2, 206 2, 602 21 21 1, 079 13, 201 Dev. TOT=Dev. REGR+Dev. RES 14, 28 = 13, 201 + 1, 079 • DEV(Y) = 7 (1, 428)2 =14, 28 My = 3

Relazione tra indice di determinazione δ e coefficiente di correlazione lineare rxy • δ = rxy 2 • Nell’esempio precedente = (0, 9615)2 = 0, 924

Relazione tra δ e rxy

Esempio 7 supermercati (continua). Diagnostiche sui residui xi Residui A 10 0, 09 B 18 -0, 30 C 20 -0, 59 D 8 0, 09 E 30 0, 43 F 12 0, 59 G 14 -0, 30 Tot. 112 0 • Modello soddisfacente: distribuzione casuale dei residui → componente erratica

ESTRAPOLAZIONE • Si tenta di valutare in maniera attendibile il valore che assumerà la variabile dipendente in corrispondenza di un valore noto della variabile esplicativa. • CONDIZIONI – Validità della retta di regressione ( prossimo ad 1) – valore noto della variabile esplicativa non lontano dai valori utilizzati nel calcolo della retta

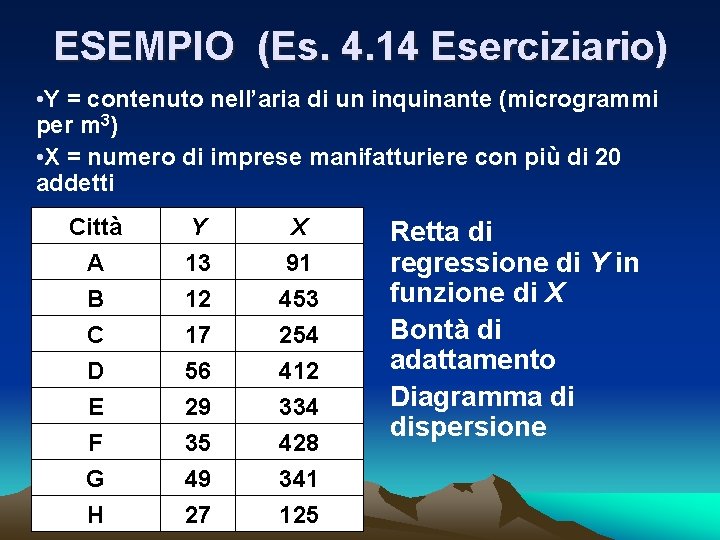
ESEMPIO (Es. 4. 14 Eserciziario) • Y = contenuto nell’aria di un inquinante (microgrammi per m 3) • X = numero di imprese manifatturiere con più di 20 addetti Città A B C Y 13 12 17 X 91 453 254 D E F G H 56 29 35 49 27 412 334 428 341 125 Retta di regressione di Y in funzione di X Bontà di adattamento Diagramma di dispersione

Dalle formule (o calcolatrice o Excel) • a = 15, 31 • b = 0, 0474 • Interpretazione • oppure Adattamento scadente

Scatter (x, y) con retta di regressione

Esercizio: giocatori titolari d’una squadra di pallavolo: la seguente tabella riporta il numero di punti segnati in attacco ed il numero di punti segnati a muro in una partita. Giocatore Punti segnati in attacco Punti segnati a muro A 14 4 B 10 3 C 4 1 D 15 1 E 18 2 F 9 5 • Calcolare rxy e commentarlo • Diagramma di dispersione. • Si confrontino le informazioni traibili dal diagr. di dispersione con il valore prima calcolato di rxy. C’è accordo tra le due analisi? A quale causa possono essere imputate le differenze riscontrate?

L’INTERPOLAZIONE DI UNA SERIE STORICA

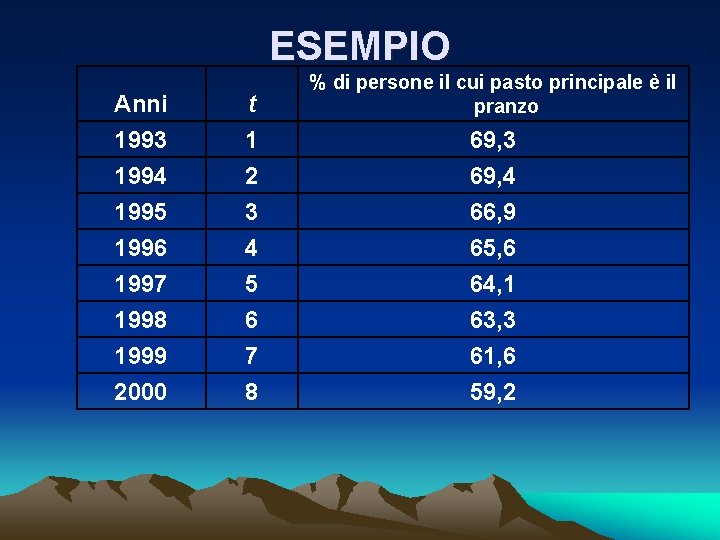
ESEMPIO Anni 1993 1994 t 1 2 1995 1996 1997 1998 1999 2000 3 4 5 6 7 8 % di persone il cui pasto principale è il pranzo 69, 3 69, 4 66, 9 65, 6 64, 1 63, 3 61, 6 59, 2

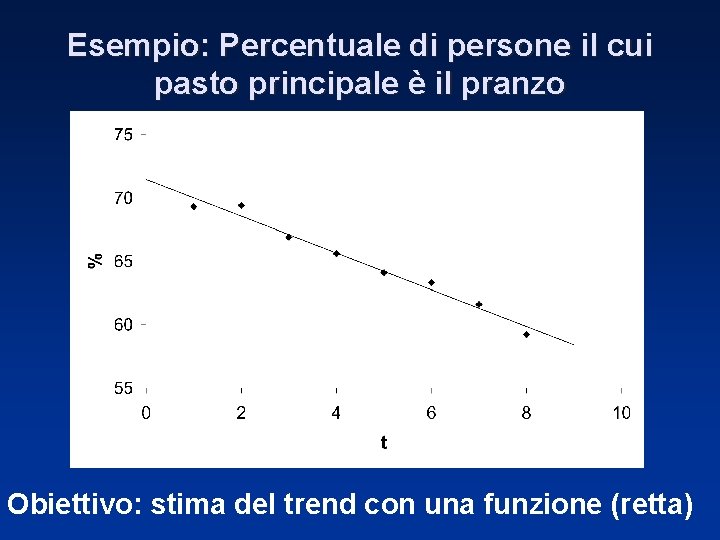
Esempio: Percentuale di persone il cui pasto principale è il pranzo Obiettivo: stima del trend con una funzione (retta)

Regressione in cui: • Variabile dipendente: fenomeno di cui si stima il trend (Y) • Variabile esplicativa: tempo successione convenzionale: t = 1; t = 2; … t=T Tempi 1 … t Valori di Y y 1 … yt … T … y. T

Funzione interpolante lineare: • Stima parametri: metodo dei minimi quadrati • Interpretazione parametri

Stima parametri: metodo dei minimi quadrati

Stima parametri: metodo dei minimi quadrati

Interpretazione parametri • a = valore teorico del fenomeno per t=0 (tempo precedente al primo considerato) l’intercetta ha sempre un significato operativo • b = variazione teorica media da un tempo al successivo

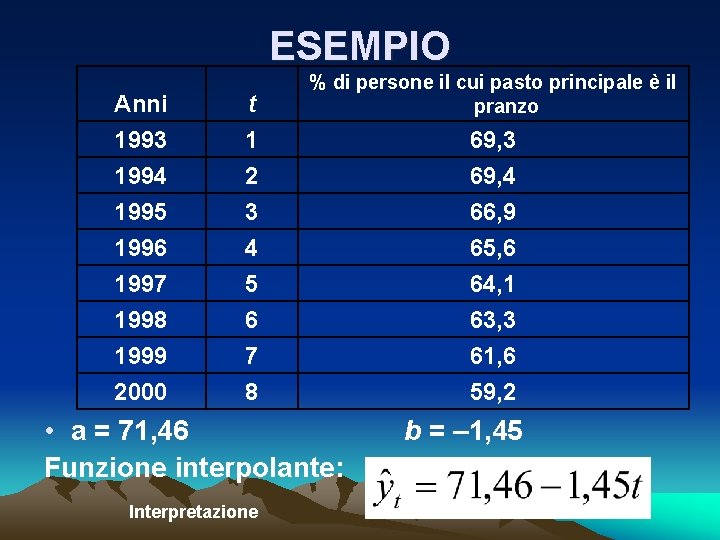
ESEMPIO Anni 1993 1994 t 1 2 1995 1996 1997 1998 1999 2000 3 4 5 6 7 8 % di persone il cui pasto principale è il pranzo • a = 71, 46 Funzione interpolante: Interpretazione 69, 3 69, 4 66, 9 65, 6 64, 1 63, 3 61, 6 59, 2 b = – 1, 45

Bontà di adattamento: • Previsione di valori futuri • Esempio: % stimata di persone il cui pasto principale è il pranzo nel 2001 (t=9):

Condizioni per la validità della proiezione • elevato • Mantenimento nel futuro delle condizioni che hanno determinato l’andamento passato funz. interpolante lineare: variazioni di ammontare costante b

Significato della proiezione • I valori futuri stimati per estrapolazione dovranno essere correttamente intesi come valutazioni non di ciò che accadrà, ma di ciò che dovrebbe accadere, qualora si manifestassero anche in futuro le condizioni che hanno determinato la precedente evoluzione del fenomeno.

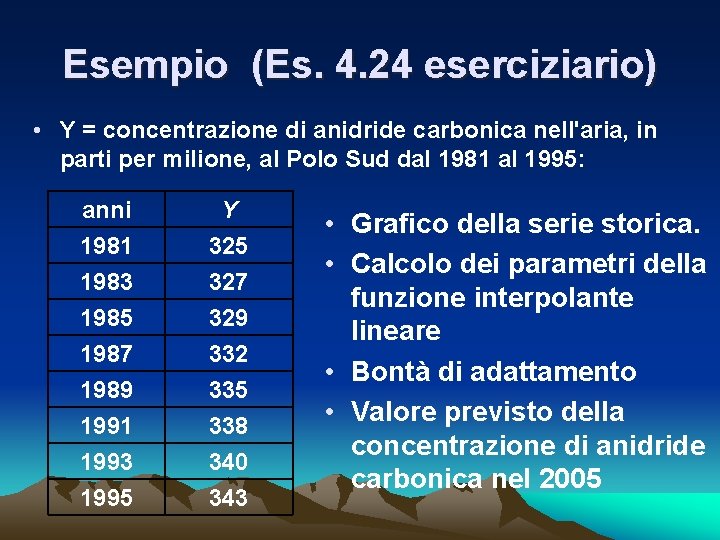
Esempio (Es. 4. 24 eserciziario) • Y = concentrazione di anidride carbonica nell'aria, in parti per milione, al Polo Sud dal 1981 al 1995: anni 1981 1983 1985 Y 325 327 329 1987 1989 1991 1993 1995 332 335 338 340 343 • Grafico della serie storica. • Calcolo dei parametri della funzione interpolante lineare • Bontà di adattamento • Valore previsto della concentrazione di anidride carbonica nel 2005

Grafico della serie storica.

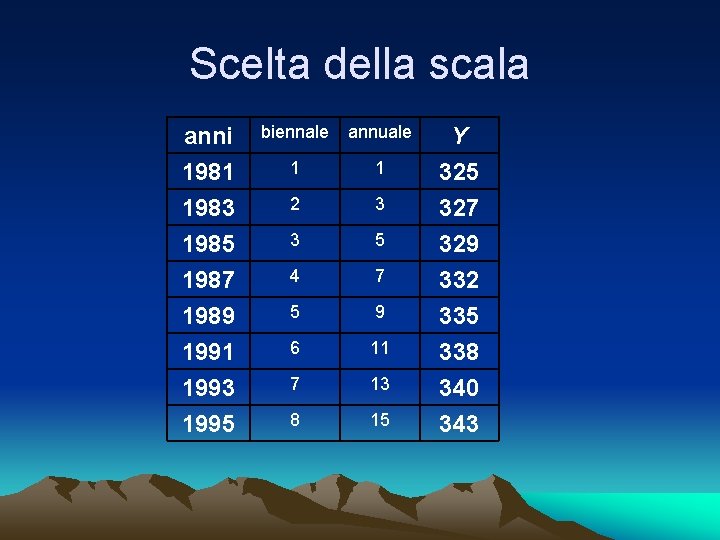
Scelta della scala anni 1981 1983 1985 biennale annuale 1 1 2 3 3 5 1987 1989 1991 1993 1995 4 7 5 9 6 11 7 13 8 15 Y 325 327 329 332 335 338 340 343

Calcolo dei parametri della funzione interpolante lineare • Scala dei tempi biennale t = 1, 2, 3, 4, 5, 6, 7, 8 • Scala dei tempi annuale t = 1, 3, 5, 7, 9, 11, 13, 15 Interpretazione

Relazione tra le due intercette anni 1981 1983 1985 1987 1989 1991 1993 1995 • Scala biennale 321, 786 = valore teorico al 1979 • Scala annuale 323, 101 = valore teorico al tempo t = 1980

Relazione tra le due intercette • 321, 786= valore teorico 1979= valore teorico 1980 - variazione teorica da un anno al successivo • variazione teorica da un anno al successivo = coeff. angolare della regressione su scala annuale • 321, 786=323, 101 -1, 3155

Bontà di adattamento • In entrambi i casi: d = 0, 996 Adattamento quasi perfetto

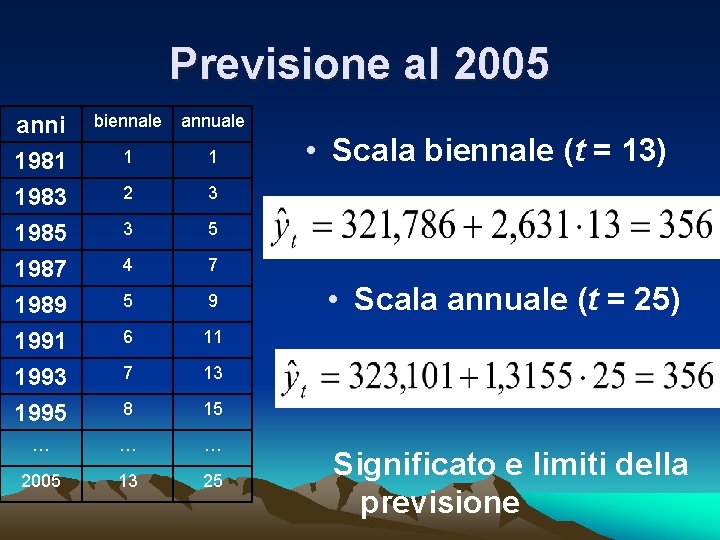
Previsione al 2005 anni 1981 1983 1985 biennale annuale 1 1 2 3 3 5 1987 1989 1991 1993 1995 4 7 5 9 6 11 7 13 8 15 … … … 2005 13 25 • Scala biennale (t = 13) • Scala annuale (t = 25) Significato e limiti della previsione

Esercizio: idrocarburi estratti (in milioni di tonnellate) n. 13 (integrativi)

Serie storica delle quantità estratte di idrocarburi dal 1986 al 1998 Anno 1986 Idrocarburi estratti 15, 4 1988 1990 18, 3 1992 18, 6 1994 19, 8 1996 19, 7 1998 19, 1 • Adottando un’opportuna scala dei tempi si calcolino i parametri della funzione interpolante lineare della quantità di idrocarburi in funzione del tempo • Significato e bontà di adattamento • Si stimino gli idrocarburi estratti nel 2004 e si dica se tale stima può ritenersi attendibile
 Famiglie logiche
Famiglie logiche Equazione monomia di secondo grado
Equazione monomia di secondo grado Esempi di relazioni sui laboratori formativi
Esempi di relazioni sui laboratori formativi Proprietà riflessiva
Proprietà riflessiva Equazioni di poisson termodinamica
Equazioni di poisson termodinamica Il gruppo di lavoro e le relazioni
Il gruppo di lavoro e le relazioni Chiara pagani
Chiara pagani Relazioni sociali roma
Relazioni sociali roma Relazioni istituzionali e responsabilita' sociale d'impresa
Relazioni istituzionali e responsabilita' sociale d'impresa Relazioni uno a molti
Relazioni uno a molti Relazioni umane
Relazioni umane Entit
Entit Relazioni economiche internazionali sbocchi
Relazioni economiche internazionali sbocchi Tulio fenomeni
Tulio fenomeni Fenomeni abiotici consecutivi
Fenomeni abiotici consecutivi Campo magnetico zanichelli
Campo magnetico zanichelli Nikolsky fenomeni
Nikolsky fenomeni Yüksük tırnak
Yüksük tırnak Paesaggio modellato da forze esogene
Paesaggio modellato da forze esogene Studia con metodi matematici fenomeni collettivi
Studia con metodi matematici fenomeni collettivi Dawn fenomeni ve somogy etkisi
Dawn fenomeni ve somogy etkisi Krški reljefni oblici
Krški reljefni oblici Legge di faraday
Legge di faraday Coulomb unità di misura
Coulomb unità di misura Krški fenomeni gorske hrvatske
Krški fenomeni gorske hrvatske Rizartroz
Rizartroz Fenomeni pericolosi per il volo
Fenomeni pericolosi per il volo Somogy fenomeni
Somogy fenomeni Spee wilson eğrisi nedir
Spee wilson eğrisi nedir Titübasyon nedir
Titübasyon nedir Ondülans ateş
Ondülans ateş Brudzinski bacak fenomeni
Brudzinski bacak fenomeni Differenza tra sistema informatico e informativo
Differenza tra sistema informatico e informativo Tra
Tra Differenze tra scuola siciliana e dolce stil novo
Differenze tra scuola siciliana e dolce stil novo Conto economico e patrimoniale
Conto economico e patrimoniale Tra
Tra Micerino tra due dee
Micerino tra due dee Bảng nhân 3
Bảng nhân 3 Kim tra
Kim tra Differenze chanson de geste e romanzo cortese
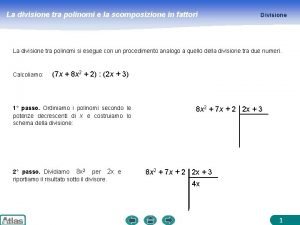
Differenze chanson de geste e romanzo cortese Scomposizione polinomi
Scomposizione polinomi Notazione esponenziale e scientifica differenza
Notazione esponenziale e scientifica differenza Siox trä
Siox trä Piaget freud
Piaget freud Chọn câu trả lời
Chọn câu trả lời Non c'è dialogo nella coppia
Non c'è dialogo nella coppia Precursore del naturalismo
Precursore del naturalismo Tra
Tra Valutazione autentica
Valutazione autentica Istorija pretrage interneta
Istorija pretrage interneta Di a da in con su per
Di a da in con su per Epica classica
Epica classica Illuminismo vs romanticismo
Illuminismo vs romanticismo Distico elegiaco
Distico elegiaco Differenza tra pressione assoluta e relativa
Differenza tra pressione assoluta e relativa Differenza tra sistemi e apparati
Differenza tra sistemi e apparati Differenza tra classificazione e seriazione
Differenza tra classificazione e seriazione Quale fu il rapporto tra i tiranni è il demos
Quale fu il rapporto tra i tiranni è il demos I giusti tra le nazioni scuola primaria
I giusti tra le nazioni scuola primaria Tra bong vietnam
Tra bong vietnam Carmen lxxii
Carmen lxxii Tra bài
Tra bài Differenza tra aggettivo e pronome possessivo
Differenza tra aggettivo e pronome possessivo Accusativo complemento oggetto
Accusativo complemento oggetto Equazioni bisettrici quadranti
Equazioni bisettrici quadranti Sammansatta sockerarter
Sammansatta sockerarter Nêu các bước nhập công thức vào ô tính
Nêu các bước nhập công thức vào ô tính Istogramma ortogramma differenza
Istogramma ortogramma differenza Differenza tra vas e via
Differenza tra vas e via Differenza tra prima e seconda sofistica
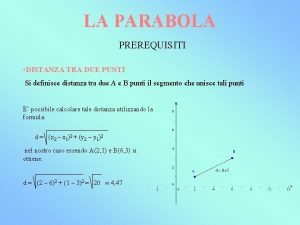
Differenza tra prima e seconda sofistica Distanza punto piano
Distanza punto piano Differenza tra dsa e bes
Differenza tra dsa e bes Analisi testo narrativo
Analisi testo narrativo Distanza tra due punti piano cartesiano
Distanza tra due punti piano cartesiano Tra n e o greca
Tra n e o greca La costituzione italiana struttura
La costituzione italiana struttura Logica programmata
Logica programmata Tra tre tri tro tru imagenes
Tra tre tri tro tru imagenes Tra
Tra Proporzione continua come si risolve
Proporzione continua come si risolve Foscolo neoclassicismo e preromanticismo
Foscolo neoclassicismo e preromanticismo Allitterazione poesia
Allitterazione poesia Fac simile dichiarazione di intesa
Fac simile dichiarazione di intesa Gerundio gerundivo
Gerundio gerundivo Verifica testo narrativo sequenze personaggi
Verifica testo narrativo sequenze personaggi Legame covalente apolare
Legame covalente apolare Dexieume
Dexieume Unione tra due insiemi
Unione tra due insiemi Differenza tra facilitazione e semplificazione
Differenza tra facilitazione e semplificazione Sistema di riferimento cartesiano
Sistema di riferimento cartesiano Sentimenti significato
Sentimenti significato Ruffini metodo
Ruffini metodo Distanza fra due punti
Distanza fra due punti Tra ch
Tra ch Prodotto tra logaritmi
Prodotto tra logaritmi Differenza tra gnss e gps
Differenza tra gnss e gps Sostantivi in alfa impuro breve
Sostantivi in alfa impuro breve Coordinazione intersegmentaria omologa esempi
Coordinazione intersegmentaria omologa esempi Disegni longitudinali
Disegni longitudinali