Relativity Visual Guide to Special and General Relativity

Relativity Visual Guide to Special and General Relativity

Get Ready…. This is about to get weird…

Groundwork for relativity �Michelson-Morley contradicted Newton �Radioactivity (the energy released didn’t match up with the energy of the atoms) �Emission spectra of blackbodies �Atomic Emission Spectra

Michelson-Morley

Results of Michelson-Morley �There is no ether �Speed of light defies Newton’s predictions

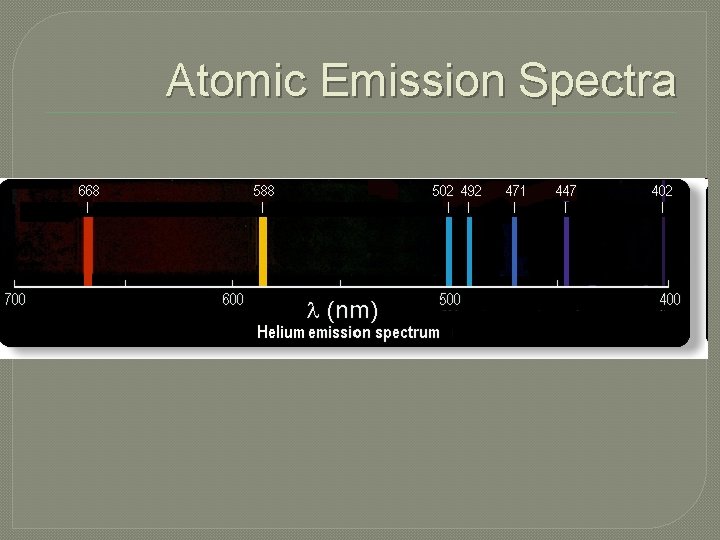
Atomic Emission Spectra

Bohr failed to explain emission spectra

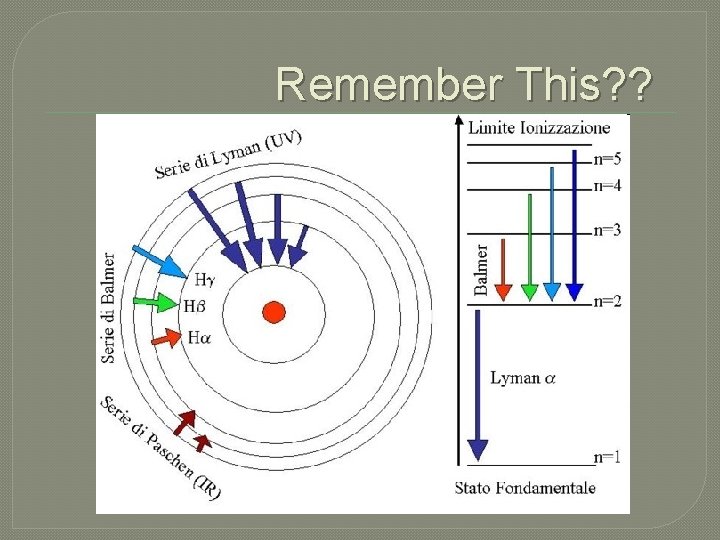
Remember This? ?

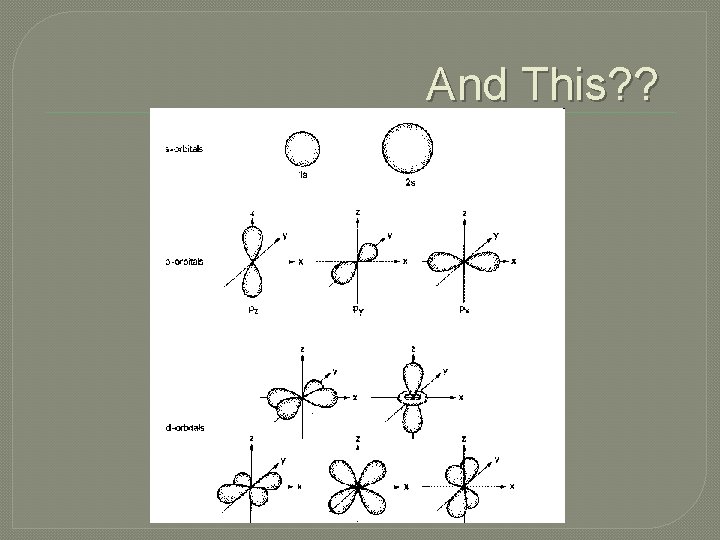
And This? ?

The man himself!

Just showing that he is smarter than the rest of us…

General Relativity � Applies to accelerated reference frames � The Principle of Equivalence • All experiments conducted in a gravitational field and in an accelerated reference frame give identical results � This means that if you dropped a ball in an elevator, you would have no way of knowing if you were in a gravitational field or being accelerated through space

Consequences of General Relativity �Black Holes �Gravitational �New �An lensing perception of gravity idea well before its time!

The Postulates of Special Relativity �Equivalence of Physical Laws • The laws of Physics are the same in all inertial frames of reference • (An inertial reference frame is a reference frame with no acceleration) �Constancy of the speed of light • The speed of light in a vacuum is the same in all reference frames, independent of the motion of the observer

First Postulate �Specific Example: • An object at rest with no forces acting on it will have zero acceleration in all reference frames

Second Postulate � All observers in all reference frames agree that light waves move at 3. 00 x 108 m/s regardless of their own motion. � Example � If spaceship A, traveling close to the speed of light) flies past a stationary astronaut and fires a laser beam straight ahead as it passes, how fast will the laser beam travel according to the spaceship pilot? The astronaut?

The speed of light, c, is the upper limit to velocity �Nothing can move faster than light. �All observers in all reference frames agree. �In order for this to be true, Einstein posed that both time and space are relative!!

Relativity of Time �As objects approach the speed of light, relativistic time dilation becomes significant. �Consider a plane flying very fast at a very high altitude.

Time is Relative �Time is not the same for all observers. �The faster an object moves, the slower time gets for that object (relative to a stationary observer) �An observer on the moving object, perceives time to move normally for him or herself

What happens if an object were able to travel faster than light? �It would travel back in time!!! �Tachyons are particles that do just that… • We don’t know much about them

Time Dilation Time in moving reference frame Time in inertial reference frame Velocity of the moving object Speed of light (1 – v 2/c 2)-1/2 can be written as γ (gamma) This is called the Lorentz Transformation

A space ship carrying a light clock moves with a speed of 0. 500 c relative to an observer on Earth. According to this observer, how long does it take for the spaceship’s clock to advance 1. 00 s? Solution: Insert ∆t = 1. 00 s and v = 0. 500 c into the equation and get:

Elephants have a gestation period of 21 months. Suppose that a freshly impregnated elephant is placed on a spaceship and sent toward a distant space jungle at v = 0. 75 c. How long will scientists on the distant planet have to wait until the spaceship lands exactly 21 months later? Solution: 31. 7 months

The Twins Paradox Omar and Maurice are identical twins. Omar gets on a spaceship and travels at a high speed to a star far outside our solar system and returns to Earth while his twin brother Maurice remains at home. When they greet each other, Maurice will be very much older than Omar. How can this be?

Watch Conceptual Physics DVD Example: If Omar and Maurice are both 17. 0 years old when Omar leaves on his space journey, and he travels at 0. 990 c to Vega (a star 26. 4 ly distant), a) How long does the trip take from Maurice’s point of view?

Example problem: b) How much has Omar aged when he reaches Vega? **When Omar Reaches Vega, he is 20. 77 years old; Maurice is 43. 7 years old!

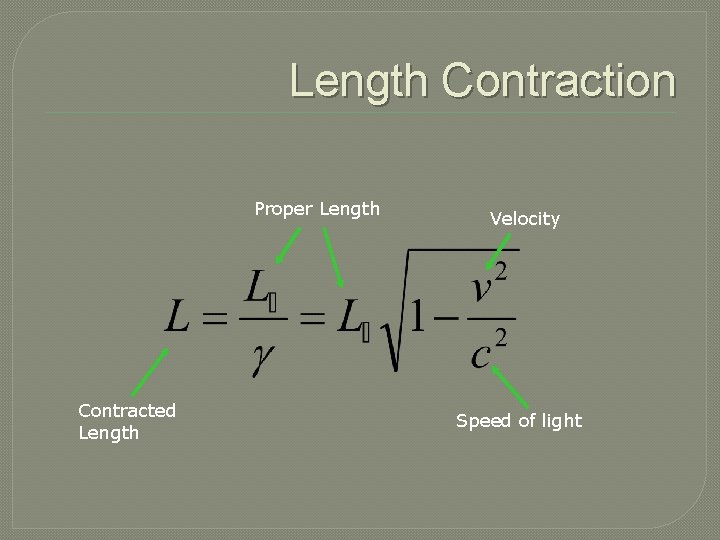
Length is Relative!! � Since time dilates for objects traveling at near light speed, Length must also contract � This prediction of Einstein’s that coincides with time dilation � Length only contracts in the direction of motion. � E. g. if the object is moving in the x direction, the height in the y direction is unaffected

http: //www. glenbrook. k 12. il. us/gbssci/phys/mmedia/specrel/Lc. html

Length Contraction Proper Length Contracted Length Velocity Speed of light

Example: Find the speed for which the length of a meter stick is 0. 500 m 1. 00 m 0. 500 m v Solve for v:

Addition of Velocities Suppose you are the pilot of a space shuttle in deep space, moving toward an asteroid with a speed of 25 mi/h. To signal a colleague on the asteroid, you activate a beam of light from the front of your shuttle. Classical physics predicts that the velocity of the light beam would be 25 mi/h + c. Relativity states this is impossible because nothing can travel with a speed greater than c. How fast then, does the beam of light travel? Is its speed different for you than it is for your colleague?

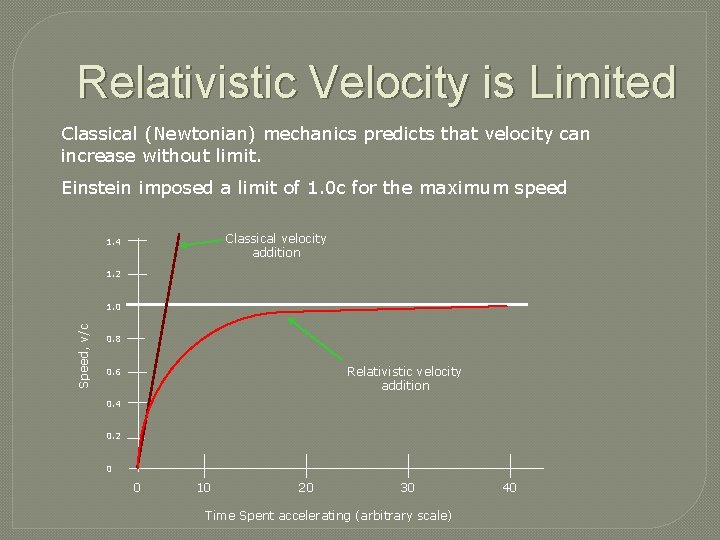
Relativistic Velocity is Limited Classical (Newtonian) mechanics predicts that velocity can increase without limit. Einstein imposed a limit of 1. 0 c for the maximum speed Classical velocity addition 1. 4 1. 2 Speed, v/c 1. 0 0. 8 Relativistic velocity addition 0. 6 0. 4 0. 2 0 0 10 20 30 Time Spent accelerating (arbitrary scale) 40

Relativistic Addition of Velocities Velocity of Moving object A (relative to a stationary observer) Velocity of Moving object B (relative to a stationary observer) Velocity of objects A & B relative to each other Speed of light **Assume Object A is the spaceship, object B is the light beam, the colleague is the stationary observer

Example: Suppose the spaceship described in the previous example is approaching an asteroid with a speed of 0. 750 c. If the spaceship launches a probe toward the asteroid with a speed of 0. 800 c relative to the ship, what is the speed of the probe relative to the asteroid? Solution:

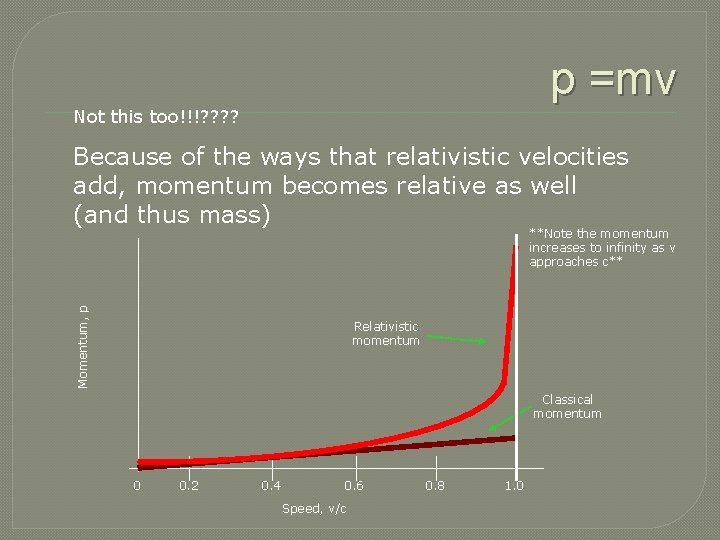
p =mv Not this too!!!? ? Because of the ways that relativistic velocities add, momentum becomes relative as well (and thus mass) Momentum, p **Note the momentum increases to infinity as v approaches c** Relativistic momentum Classical momentum 0 0. 2 0. 4 0. 6 Speed, v/c 0. 8 1. 0

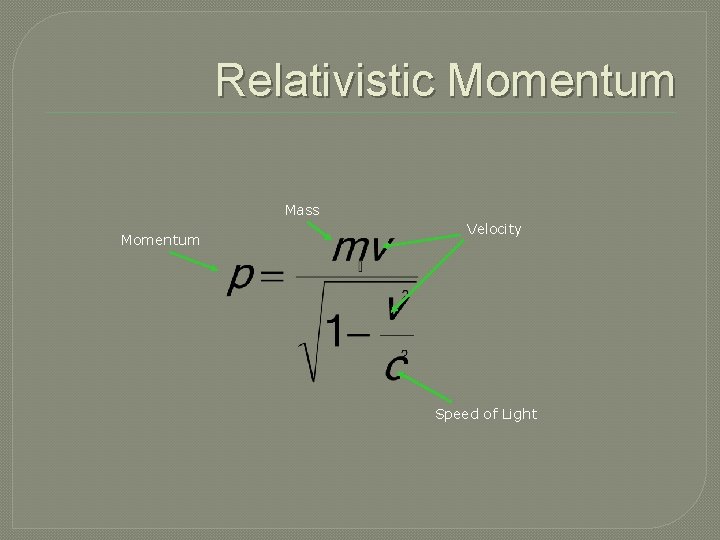
Relativistic Momentum Mass Momentum Velocity Speed of Light

Example: Find both the classical and relativistic momentum of a 2. 4 kg mass moving with a speed of 0. 81 c. Solution: Classical momentum Relativistic momentum:

Relativistic Mass A useful way to apply relativistic momentum is in terms of a mass that increases with speed. We can suppose that an object has a fixed mass when at rest; we call this rest mass. Rest mass Relativistic mass **Note that m approaches infinity as v c, thus a constant force generates less and less acceleration, a = F/m; thus the speed of light cannot be exceeded.

Relativistic Energy �You were just shown that an object’s mass increases as its velocity increases. �Thus, when work is done on an object, part of the work increases the object’s velocity, and part of the work increases the object’s mass. �Thus, mass is another form of energy!

Einstein’s Famous Equation Total Energy Rest Mass Relativistic Mass Velocity Speed of Light

Rest Energy Example: Show the expression for the rest energy of an object. That is the energy when the object’s speed is zero.

Example: Find the rest energy of a 0. 12 kg apple. Compare this with the total yearly energy usage of the US… 1020 J!!!!

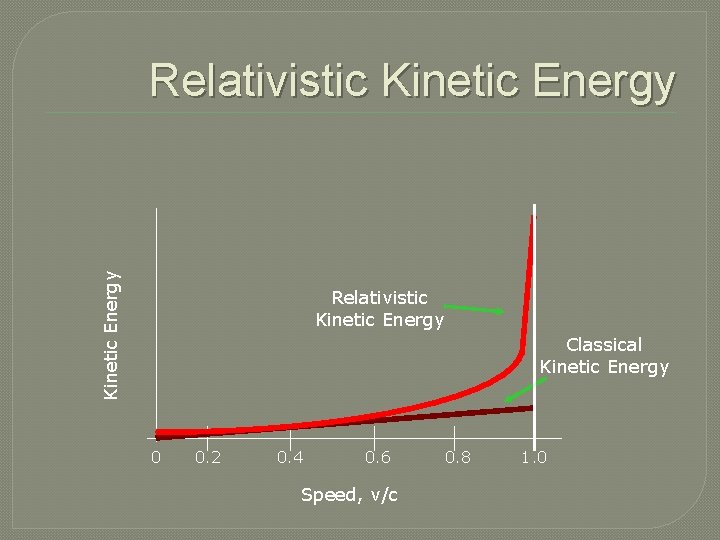
Relativistic Kinetic Energy Rest mass Kinetic Energy

Kinetic Energy Relativistic Kinetic Energy Classical Kinetic Energy 0 0. 2 0. 4 0. 6 Speed, v/c 0. 8 1. 0

Consequences of Relativity �It is impossible to exceed the speed of light �When approaching the speed of light, an object gains an infinite mass �An infinite amount of energy must be applied to allow the object to reach the speed of light. �This, no object with a mass can actually reach the speed of light