Relationships Within Triangles Chapter 5 5 1 Midsegment

5. 1 – Midsegment Theorem � Midsegment of a triangle � Segment that connects

5. 2 – Use Perpendicular Bisectors � Perpendicular bisector � Segment, ray, line, or

Theorems � Theorem 5. 2 – Perpendicular Bisector Theorem � In a plane, if

Example 1 � Line BD is the perpendicular bisector of segment AC. Find the

Concurrency of Lines, Rays & Segments � Concurrent � When three or more lines,

Theorem 5. 4 � Concurrency of Perpendicular Bisectors of a Triangle � The perpendicular

Example 3 � Three snack carts sell frozen yogurt from points A, B, and

Circumcenter � Point of concurrency of the three perpendicular bisectors of a triangle �

5. 3 – Use Angle Bisectors of a Triangle � Remember: � An angle

Theorems � Theorem 5. 5 – Angle Bisector Theorem � If a point is

Examples � Example 1 � P. 312 � Example 2 � P. 313

Example 3 � For what value of x does P lie on the bisector

Incenter of a Triangle � Theorem 5. 7 – Concurrency of Angle Bisectors of

5. 4 – Use Medians & Altitudes � Median of a triangle � Segment

Altitudes of a Triangle � Altitude of a triangle � Perpendicular segment from a

5. 5 – Inequalities in a Triangle � Theorem 5. 10 � If one

Triangle Inequality Theorem � Theorem 5. 12 – Triangle Inequality Theorem � The sum

Slides: 21

Download presentation

Relationships Within Triangles Chapter 5

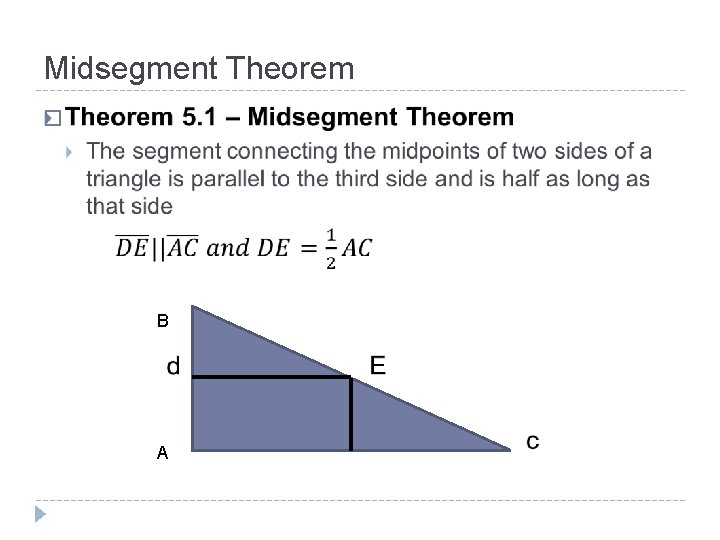
5. 1 – Midsegment Theorem � Midsegment of a triangle � Segment that connects midpoints of two sides of a triangle � Every triangle has three midsegments

Midsegment Theorem � B A

5. 2 – Use Perpendicular Bisectors � Perpendicular bisector � Segment, ray, line, or plane that is perpendicular to a segment at its midpoint � Equidistant � Points on the perpendicular bisector of a segment are the same distance from the segment’s endpoints

Theorems � Theorem 5. 2 – Perpendicular Bisector Theorem � In a plane, if a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment � Theorem 5. 3 – Converse of the Perpendicular Bisector Theorem � In a plane, if a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment

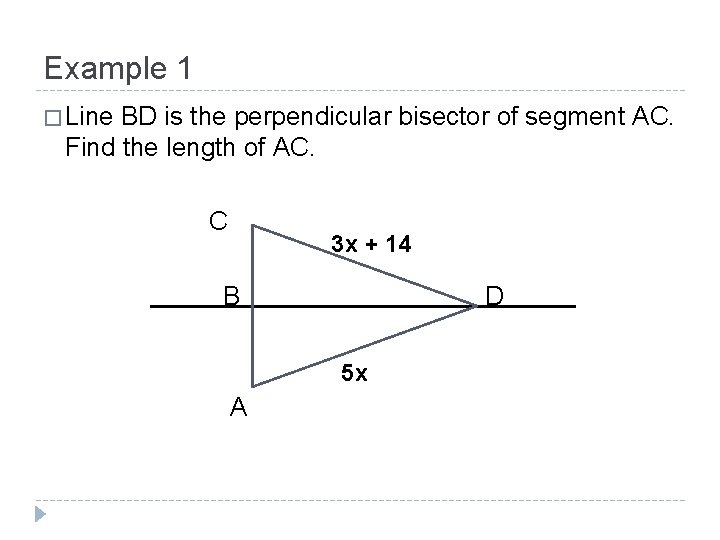
Example 1 � Line BD is the perpendicular bisector of segment AC. Find the length of AC. C 3 x + 14 B D 5 x A

Concurrency of Lines, Rays & Segments � Concurrent � When three or more lines, rays, or segments intersect in the same point � Point of concurrency � Point of intersection of three or more lines, rays, or segments

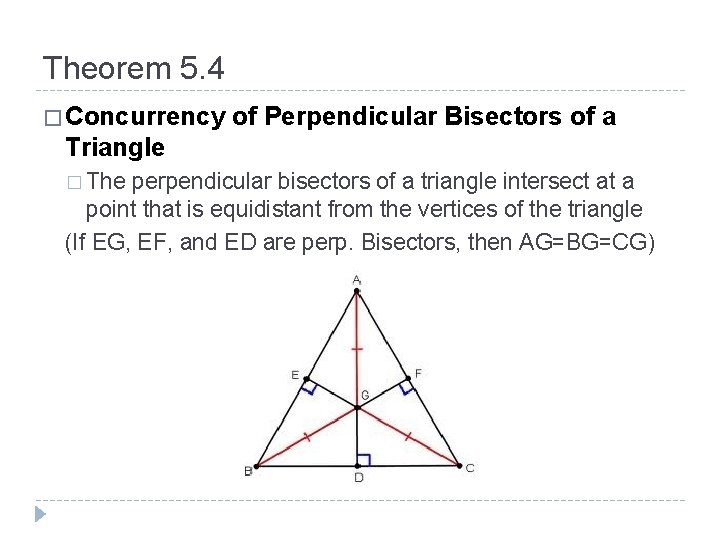
Theorem 5. 4 � Concurrency of Perpendicular Bisectors of a Triangle � The perpendicular bisectors of a triangle intersect at a point that is equidistant from the vertices of the triangle (If EG, EF, and ED are perp. Bisectors, then AG=BG=CG)

Example 3 � Three snack carts sell frozen yogurt from points A, B, and C outside a city. Each of the three carts is the same distance from the frozen yogurt distributor (D) � Find a location for the distributor that is equidistant from the three carts � (you will draw on the next slide)

Circumcenter � Point of concurrency of the three perpendicular bisectors of a triangle � Activity: � Construct the perpendicular bisectors of a triangle, and check to see if a circle can be constructed so that all vertices of the triangle lie on the circle

5. 3 – Use Angle Bisectors of a Triangle � Remember: � An angle bisector is a ray that divides an angle into two congruent adjacent angles � The distance from a point to a line is the length of the perpendicular segment from the point to the line

Theorems � Theorem 5. 5 – Angle Bisector Theorem � If a point is on the bisector of an angle, then it is equidistant from the two sides of the angle � Theorem 5. 6 – Converse of Angle Bisector Thrm. � If a point is in the interior of an angle and is equidistant from the sides of the angle, then it lies on the bisector of the angle

Examples � Example 1 � P. 312 � Example 2 � P. 313

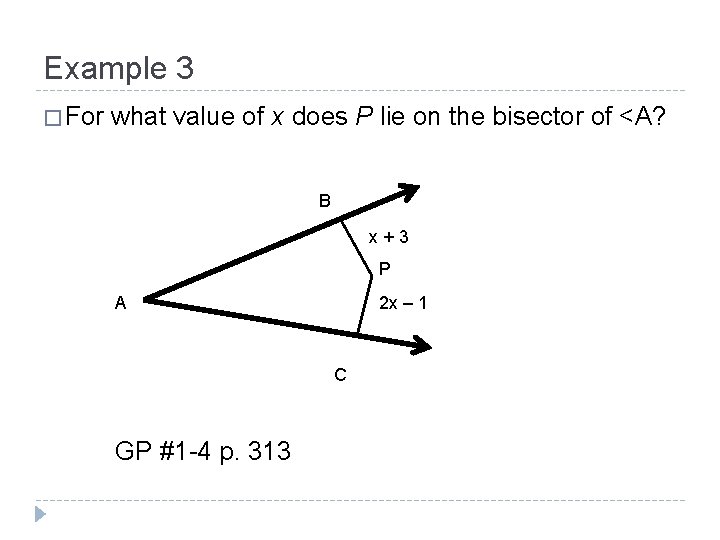
Example 3 � For what value of x does P lie on the bisector of <A? B x + 3 P A 2 x – 1 C GP #1 -4 p. 313

Incenter of a Triangle � Theorem 5. 7 – Concurrency of Angle Bisectors of a Triangle � The angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle � Incenter � Point of concurrency of the three angle bisectors of a triangle � Always lies inside the triangle � Example 4, p. 314

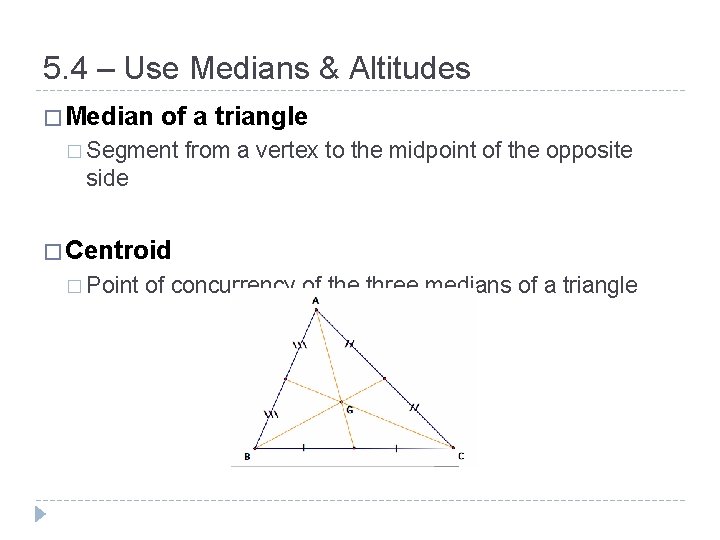
5. 4 – Use Medians & Altitudes � Median of a triangle � Segment from a vertex to the midpoint of the opposite side � Centroid � Point of concurrency of the three medians of a triangle

Theorem �

Altitudes of a Triangle � Altitude of a triangle � Perpendicular segment from a vertex to the opposite side of to the line that contains the opposite side � Theorem 5. 9 – Concurrency of Altitudes of a Triangle � The lines containing the altitudes of a triangle are concurrent � Orthocenter � Point at which the lines containing the three altitudes of a triangle intersect

5. 5 – Inequalities in a Triangle � Theorem 5. 10 � If one side of a triangle is longer than another side, then the angle opposite the longer side is larger than the angle opposite the shorter side � Theorem 5. 11 � If one angle of a triangle is larger than another angle, then the side opposite the larger angle is longer than the side opposite the smaller angle

Triangle Inequality Theorem � Theorem 5. 12 – Triangle Inequality Theorem � The sum of the lengths of any two sides of a triangle is greater than the length of the third side � Example 3 � A triangle has one side of length 12 and another length 8. Describe the possible lengths of the third side. GP #3 p. 332