Relationship between E and V potential Gradient Q

Relationship between E and V – potential Gradient

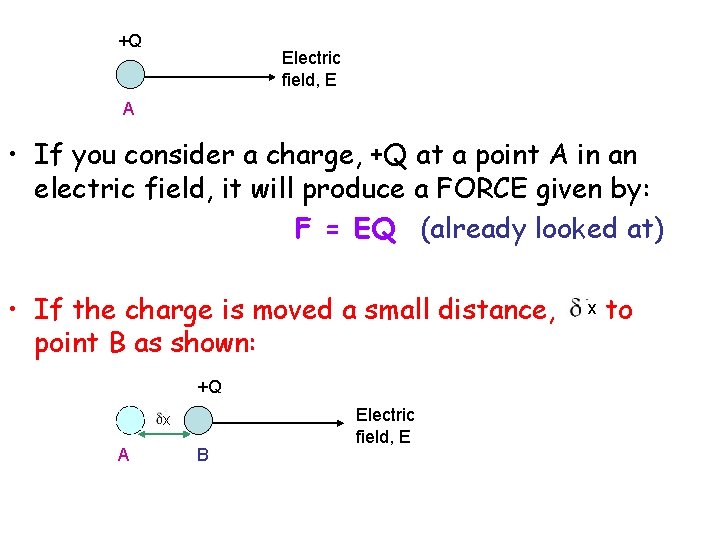
+Q Electric field, E A • If you consider a charge, +Q at a point A in an electric field, it will produce a FORCE given by: F = EQ (already looked at) • If the charge is moved a small distance, point B as shown: +Q x A B Electric field, E x to

• Then the WORK DONE electric force on Q is: W W W = force x distance But F = EQ =F x = E Q x (1) W by the

• The definition of potential difference between two points is: The work done per unit charge in moving a small positive charge between the points: i. e. W Q = The small potential between A and B V Sub in equation (1) V = -E x The –ve sign is inserted to show that if displacements in the direction of E are taken to be +ve, then when x iis +ve, V is –ve, i. e. the potential decreases.

• If the charge is moving in the opposite direction to E, then x is –ve, and V is +ve, therefore potential INCREASES. • In the limit, as x 0 , E becomes the field strength at a point (A) and so: E = - d V dx Potential gradient in the xdirection Potential gradient is a VECTOR and is measured in volts per metre (Vm-1) or (NC-1)

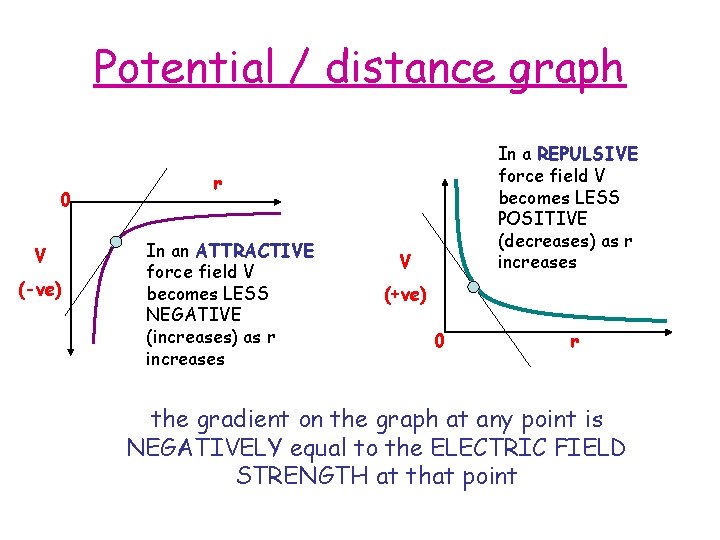
Potential / distance graph 0 V (-ve) In a REPULSIVE force field V becomes LESS POSITIVE (decreases) as r increases r In an ATTRACTIVE force field V becomes LESS NEGATIVE (increases) as r increases V (+ve) 0 r the gradient on the graph at any point is NEGATIVELY equal to the ELECTRIC FIELD STRENGTH at that point

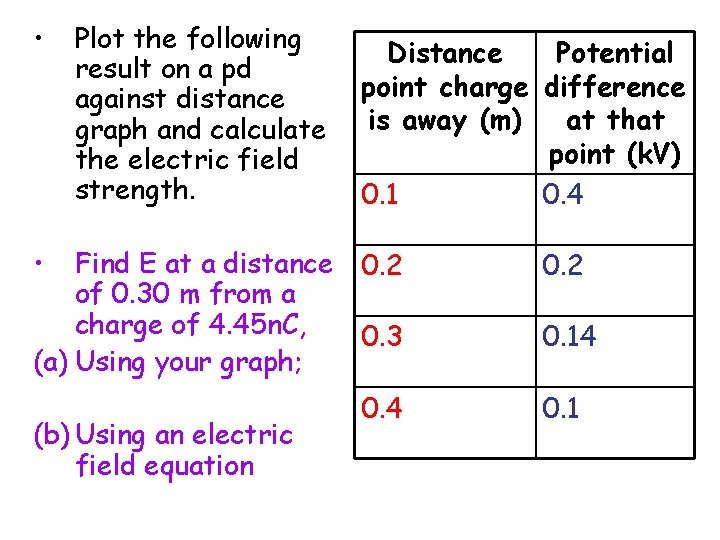
• Plot the following result on a pd against distance graph and calculate the electric field strength. • Find E at a distance of 0. 30 m from a charge of 4. 45 n. C, (a) Using your graph; (b) Using an electric field equation Distance Potential point charge difference is away (m) at that point (k. V) 0. 1 0. 4 0. 2 0. 3 0. 14 0. 1

• In a UNIFORM field, E is CONSTANT in magnitude and direction at all points, hence d. V / dx is CONSTANT. • The potential changes steadily with distance. • From earlier: E=-V/d

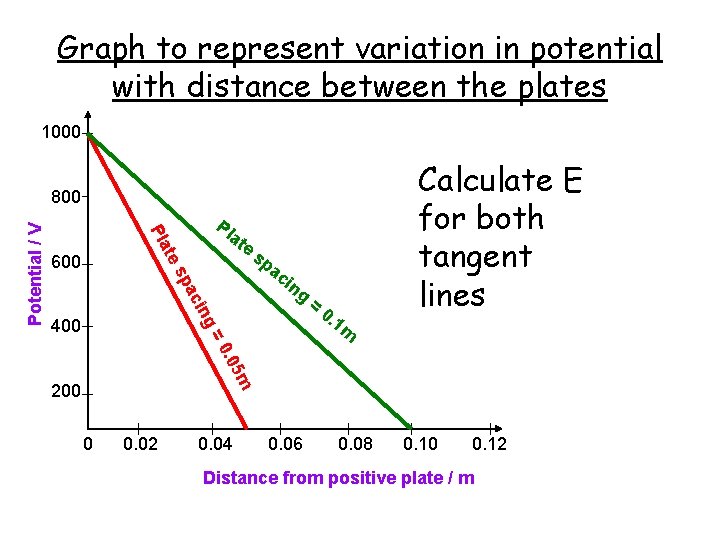
Graph to represent variation in potential with distance between the plates 1000 Pl a Pla 600 te te ing ac = 0. 1 m Calculate E for both tangent lines m . 05 =0 400 sp ac in g sp Potential / V 800 200 0 0. 02 0. 04 0. 06 0. 08 0. 10 0. 12 Distance from positive plate / m

• Plate spacing = 0. 05 m E=-V/d E = - 1000 / 0. 05 = 20, 000 V m-1 • Plate spacing = 0. 1 m E=-V/d E = - 1000 / 0. 1 = 10, 000 V m-1

• Calculate the electric field strength for plates separated at distances between 0. 2 m to 1. 6 m when the potential is 1000 V. • With these results plot a graph of Electric field strength against plate separation

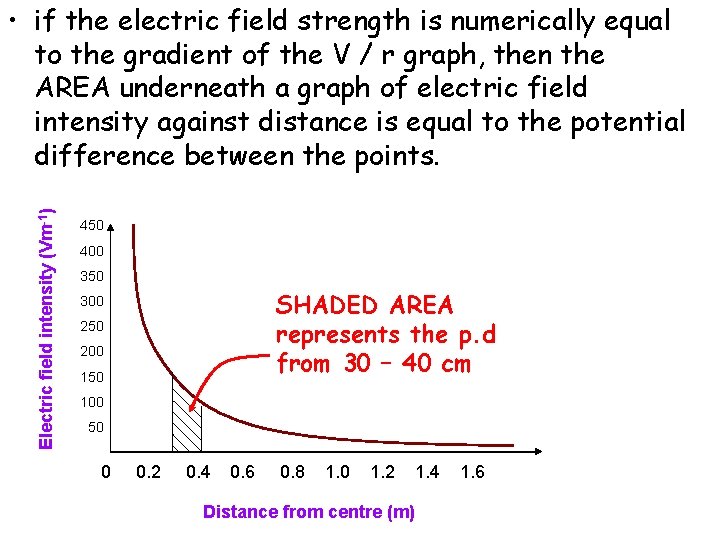
Electric field intensity (Vm-1) • if the electric field strength is numerically equal to the gradient of the V / r graph, then the AREA underneath a graph of electric field intensity against distance is equal to the potential difference between the points. 450 400 350 SHADED AREA represents the p. d from 30 – 40 cm 300 250 200 150 100 50 0 0. 2 0. 4 0. 6 0. 8 1. 0 1. 2 Distance from centre (m) 1. 4 1. 6