Relations Compare with function Function Set of ordered

Relations • Compare with function – Function: • Set of ordered pairs where x’s don’t repeat • x’s come from domain; y’s come from co-domain • Purpose: to transform input into output – Relation: • Any set of ordered pairs: the x’s may repeat • x and y must be drawn from the same set. • Purpose: to exhibit relationships among data in a set. • Examples & properties

Relations • Within some set, the elements may have some relationship • Can be depicted by – – A formula List/set of ordered pairs Directed graph Adjacency matrix 0 1 1 1 0 0 0 1 0 0 • Example: the “<“ relation on the set { 1, 2, 3, 4 } – 1 points to 2, 3, 4 – etc. • Standard notation: x. Ry means “x is related to y” where R is the name of the relation.

Examples Let S = { 1, 2, 3, 4, 5 }. Relations will be over this set. • x. Ry if y = x + 1 – A special case of a relation is a function. All functions are relations, but not all relations are functions! • x. Ry if y = x 1 0 0 0 0 1 0 1 0 0 0 0 0 1 0

Examples • R=S S – This is called the complete relation. • x. Ry if x mod 3 = y mod 3 – What if we had more numbers in S? • x. Ry = x | y 1 1 1 0 0 1 1 1 0 1 0 0 1 1 1 0 0 1 1 1 0 1 0 0 1

Properties of relations • • • Reflexive Symmetric Antisymmetric Transitive Definite Type of relation x: x. Rx x, y: x. Ry y. Rx x, y: (x y x. Ry) ~ y. Rx x, y, z: (x. Ry y. Rz) x. Rz x, y: x. Ry y. Rx Reflexive? Symmetric? Antisymmetric? Y Transitive? Definite? Equivalence relation Y Y Partial order Y Y Y Total order Y Y

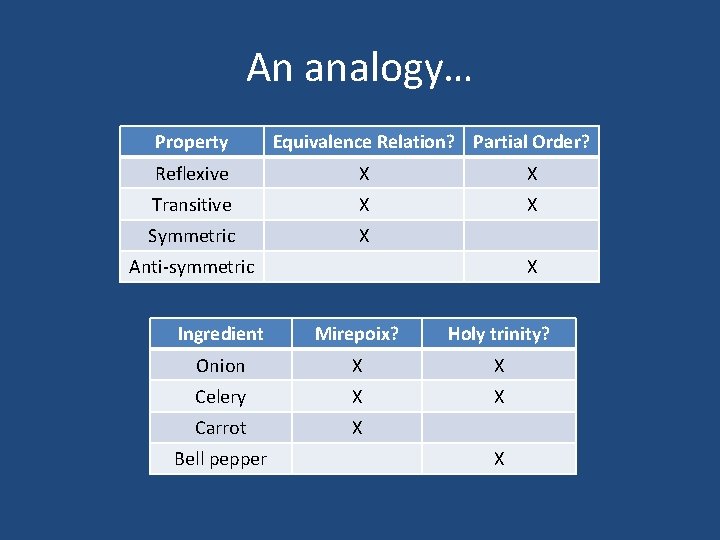
An analogy… Property Equivalence Relation? Partial Order? Reflexive X X Transitive X X Symmetric X Anti-symmetric X Ingredient Mirepoix? Holy trinity? Onion X X Celery X X Carrot X Bell pepper X

Adjacency matrix • Relation properties are sometimes easier to discern if you look at an adjacency matrix. 1 0 1 1 • Reflexive: All 1’s along main diagonal 1 0 0 • Symmetric • Anti-symmetric: Away from main diagonal, all 1’s have a 0 across the main diagonal (mirror image). • Transitive – not much help • Definite: Main diagonal is all 1’s, and for each other cell, either it or its mirror image is a 1.

Try these = < ≤ Reflexive? Symmetric? Antisymmetric? Transitive? Definite? Equiv. rel. ? Partial order? Total order? For the relational operators, let’s assume that the underlying set of objects is some subset of the integers, e. g. { 1, 2, 3 }. Same suit

Properties cont’d • Equivalence relation = a relation that is reflexive, symmetric, and transitive. – Useful when you want a collection of objects to be grouped into some partitions • What are some examples? • Partial/total order: – Useful when the set of objects need to be ranked • Many relations are possible. For example, for a set of 3 elements, you can have 512 possible relations. (Do you know why? ) However, most are not useful.

Examples of equiv. rel. • On the set of (positive) integers: – – – Same remainder when divided by 6 End in same digit Start with same digit Same number of digits Same number of divisors • On the set of people: – – – Live in same ZIP code Same sign of the zodiac Alumni of the same college Same blood type Same native language • In each case, how many equivalence classes are there?

Try this • Let S = Z Z. Let R be a relation on S such that: a. Rb if the a and b have the same Cartesian distance from (0, 0). – Show R is an equivalence relation. – Describe the equivalence classes of R.

Modulo • We can partition the set Z+ by using the mod (%) operator. • Pick a divisor, for example 5. • x. Ry if x mod 5 = y mod 5 • Equivalent definition: x. Ry if (x – y) mod 5 = 0. • What are the equivalence classes? • What if we try 10 as the divisor?