Relations Cartesian Product The Cartesian Product of A

Relations

Cartesian Product The Cartesian Product of A and B is defined as A X B = { (a, b)|a A and b B}. The Cartesian Product of n sets A 1, A 2 , A 3 , …………… An is defined as A 1 X A 2 X A 3 X ………………. . X An = { (a 1, a 2, ………an)|ai Ai , i=1, 2. . n}. The Expression (a 1, a 2, ………an) is called an ordered n-tuple. Example: Let A = { 0, 1, 2} and B = {a, b}. Then, A X B = {(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)} A X A = { (0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)}

Relations As Sets • Computing is the science (and art) of processing information. – A major concern is the relationship between different pieces of information. à Databases. • Examples of relations : – John has savings account number 333. – The File menu contains the exit option. – The root directory is the parent of the directory tree. • A binary relation can be represented as a set of pairs. – N-ary relations are simply an extension of this. 5. 3

Relations in Computing • Something like 80% of the software systems in existence involve databases. The vast majority of the databases in existence are based on relations : Relational Databases. There is a whole programming paradigm based on relations : the Relational programming languages. (PROLOG) Relational database query languages (SQL etc. ) are Relational languages. 5. 4

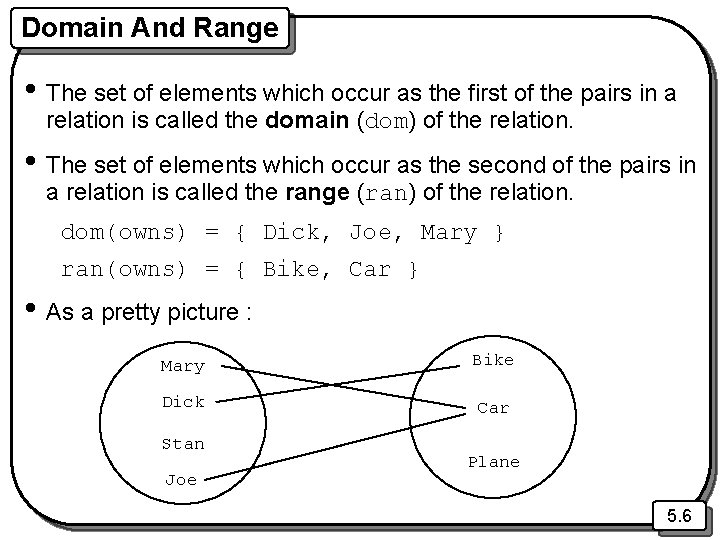
Source And Target • Assume we have a set : Transport = { Car, Bike, Horse, Plane } • The owns relation is a subset of People x Transport. owns = { (Dick, Bike), (Joe, Car), (Mary, Car) } • In this case People is the source set of the relation owns and Transport is the target set of the relation owns. • Note that not all the elements of either source or target sets needs to occur in the actual relation. – The relation may be partial. ( x Transport (Stan, x) owns) x Transport (Stan, x) owns 5. 5

Domain And Range • The set of elements which occur as the first of the pairs in a relation is called the domain (dom) of the relation. • The set of elements which occur as the second of the pairs in a relation is called the range (ran) of the relation. dom(owns) = { Dick, Joe, Mary } ran(owns) = { Bike, Car } • As a pretty picture : Mary Bike Dick Car Stan Joe Plane 5. 6

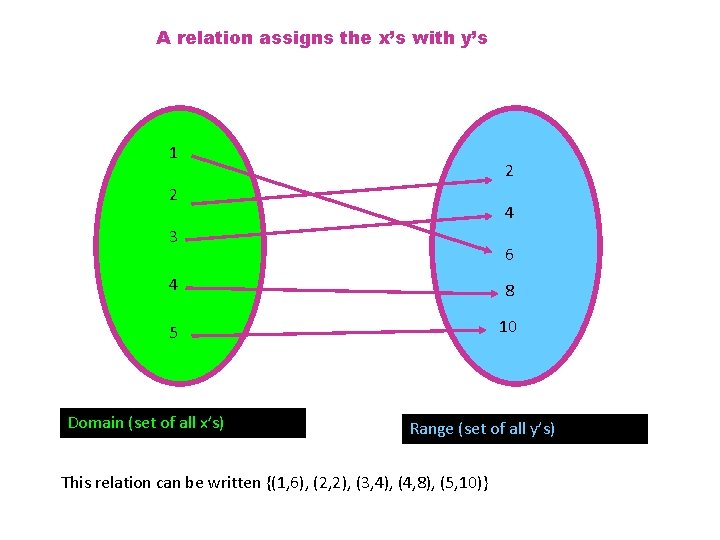
A relation is a set of ordered pairs. The domain is the set of all x values in the relation domain = {-1, 0, 2, 4, 9} These are the x values written in a set from smallest to largest {(2, 3), (-1, 5), (4, -2), (9, 9), (0, -6)} These are the y values written in a set from smallest to largest range = {-6, -2, 3, 5, 9} The range is the set of all y values in the relation Relations are theoretical basis for Relational programming languages such as Prolog and SQL. This is a relation

A relation assigns the x’s with y’s 1 2 2 4 3 6 4 8 5 10 Domain (set of all x’s) Range (set of all y’s) This relation can be written {(1, 6), (2, 2), (3, 4), (4, 8), (5, 10)}

Relational Inverse • The inverse of a relation is obtained by swapping round the components of each pair. R~ = { (1, 0), (2, 1), (5, 3) } S~ = { (2, 1), (5, 3) } • Mathematically, we can write S~ { (x, y) S (y, x) } 5. 9

Relational Composition • The composition of R with S is equal to the set of all those ordered pairs (x, z) such that we can find at least one value, say y, such that x. Ry and y. Sz. • That is R ; S { (x, y) R, (y, z) S (x, z) } • As usual, an alternative notation is sometimes used. Instead of R ; S we write S 1 thing. 0 1 3 • So R to mean the same 2 3 5 1 5 ; S = { (0, 1), (1, 1) }. 5. 10

Relational Override • This is essentially an update operation. • The override of R by S is denoted R S by adding to S all those ordered pairs from R whose first component is not in the domain of S. R S { (x, y) R x dom S } • This sounds a lot more complex than it is. Lets have an example. R = { (1, 2), (3, 4), (2, 3) } S = { (1, 6), (4, 5), (2, 7) } R S = { (1, 6), (4, 5), (2, 7), (3, 4) } • A good way to think of this is that R is the master database and S is a set of new records to be added, some of which update the data in already existing records. 5. 11

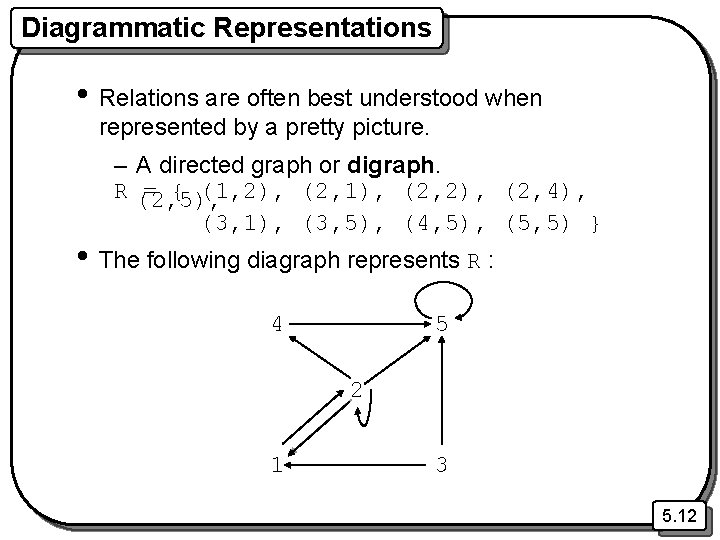
Diagrammatic Representations • Relations are often best understood when represented by a pretty picture. – A directed graph or digraph. R (2, 5), = { (1, 2), (2, 1), (2, 2), (2, 4), (3, 1), (3, 5), (4, 5), (5, 5) } • The following diagraph represents R : 4 5 2 1 3 5. 12

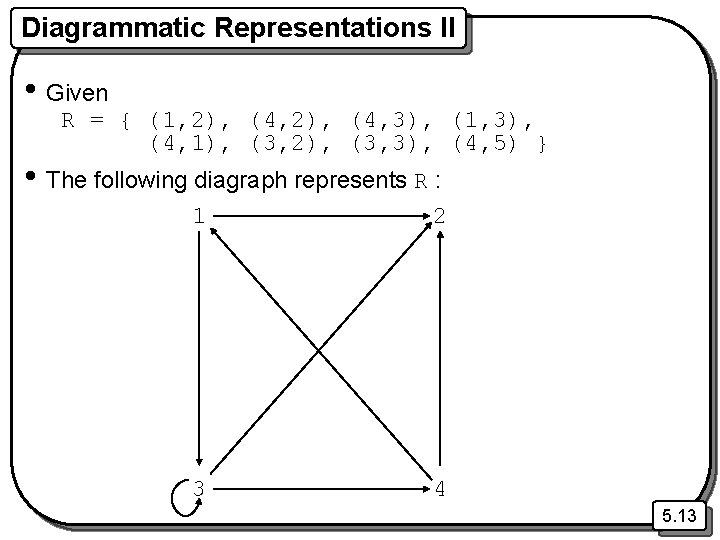
Diagrammatic Representations II • Given R = { (1, 2), (4, 3), (1, 3), (4, 1), (3, 2), (3, 3), (4, 5) } • The following diagraph represents R : 1 2 3 4 5. 13

Types Of Relations • An homogeneous relation is a binary relation in which the source and target sets are identical. R Names • Useful for things like – A family tree (parent, ancestor, married to etc. ) – Traveling problems (bus, rail and road connections etc. ) • An identity relation is a binary relation in which every element of a set is related to itself and only to itself. Ix = {x X (x, x) } • For example if X = { 0, 1, 2 } then Ix = { (0, 0), (1, 1), (2, 2) } 5. 14

Types Of Homogenous Relations • Can R = R ~? – Obviously, only for homogeneous relations. – Such a relation is called symmetric. – Given a relation R on the set X, for a symmetric relation : x, y X (x, y) R (y, x) R • Reflexive relations : every element of the domain is related to itself. Ix R – Not quite the same as a identity relation. – There may be other pairs as well. For example : R = { (1, 1), (2, 2), (1, 5), (2, 3) } 5. 15

Types Of Homogenous Relations II • If whenever a is related to b and b is related to c then a is related to c then the relation is transitive. R ; R R • If a relation is reflexive, symmetric and transitive then it is called an equivalence relation. • Given the relation R on the set { 1, 2, 3 } R = { (1, 1), (1, 2), (2, 1), (2, 2), (3, 3) } • Is this relation : – – Reflexive? Symmetric? Transitive? An equivalence relation? 5. 16

Reflexive x. Rx for all x A Symmetric If x. Ry, then y. Rx, for all x, y A Transitive If x. Ry and y. Rz, then x. Rz, for all x, y, z A Equivalence relation: Let R be a relation on A. R is an equivalence relation on A if the following conditions are satisfied: 1. x. Rx for all x A ( R is reflexive) 2. If x. Ry, then y. Rx, for all x, y A ( R is symmetric) 3. If x. Ry and y. Rz, then x. Rz, for all x, y, z A ( R is transitive) 5. 17

Example: Prove R is an equivalence relation. Let N be the set of natural numbers, that is, N = {1, 2, 3……. . }. Define a relation R in N as follows: R = {(x, y)| x, y N and x + y is even}. Example : Let A = { 1, 2, 3, 4}, and let R = { (1, 3), (4, 2), (2, 4), (2, 3), (3, 1)}. Is it R is equivalence or not Antisymmetric relation: A relation R on a set A is called an antisymmetric relation if (a, b) R and (b, a) R implies a = b. Example: R = { (1, 3), (4, 2), (2, 4), (2, 3), (3, 1)}. R is not antisymmetric because (1, 3) R and (3, 1) R, but certainly 1 ≠ 3. 5. 18

Problems 1. Let A = {1, 2, 3, 4, 5, 6}. Construct the relation R on A for the following cases. a) R = {(j, k) | j divides k} b) R = {(j, k) | j is a multiple of k} c) R = {(j, k) | (j – k)2 A} d) R = {(j, k) | j/k is a prime} 2. Let R be the relation from A = {1, 2, 3, 4, 5} to B = {1, 3, 5} which is defined by “ x is less than y. ” Write R as a set of ordered pairs. 3. Let R be the relation in the natural numbers N = {1, 2, 3, …. . } defined by “x + 2 y =10”, that is , let R = {(x, y) | x N, y N, x + 2 y = 10}. Find a) the domain and range of R b) R-1 5. 19