Relations and graphs Prof M Alonso Objectives Recognize

Relations and graphs Prof. M. Alonso

Objectives Recognize a relationship. Plot the graph of a relationship. Identify the independent variable and the dependent variable. Find the distance between two points Find the midpoint

Rectangular Coordinate System The most frequently used framework to draw a graph is called the Cartesian coordinate system or Rectangular Coordinate System.

Rectangular Coordinate System The center of the coordinate system is called the origin, which is (0, 0) It has two straight lines, perpendicular to each other, that pass through the origin. Each line is known as an axis and extends infinitely in both directions.

Rectangular Coordinate System The horizontal axis is called the x-axis, with positive numbers pointing to the right The vertical axis is the y-axis, with positive numbers pointing up.

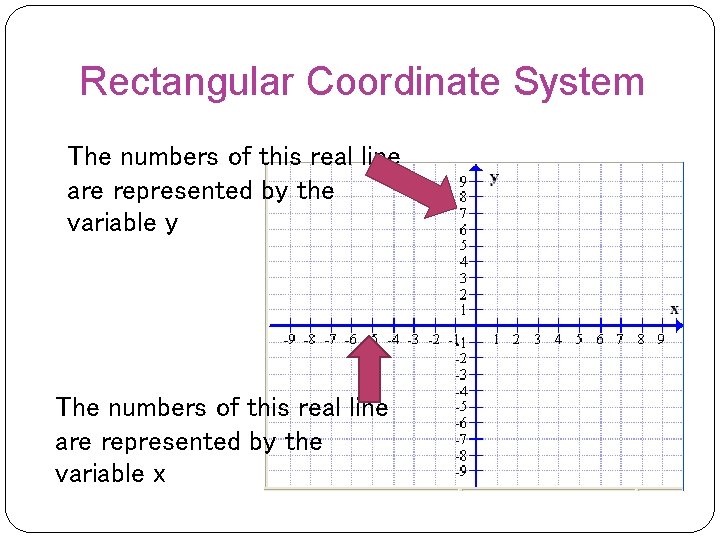
Rectangular Coordinate System The numbers of this real line are represented by the variable y The numbers of this real line are represented by the variable x

Ordered pair (a, b) What is an ordered pair? An ordered pair consists of two numbers, that's why it's called pair. It is called ordered because always the first number comes from the horizontal axis and the second number comes from the vertical axis. The symbol used is two numbers enclosed in a parenthesis (a, b)

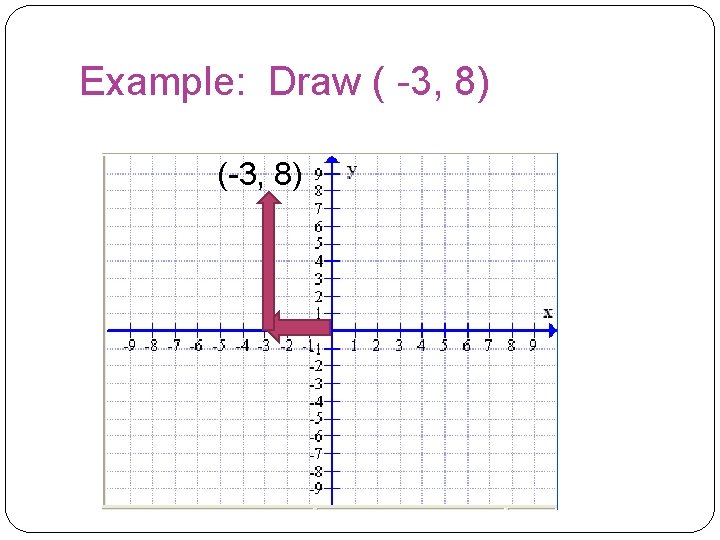
Example: Draw ( -3, 8) (-3, 8)

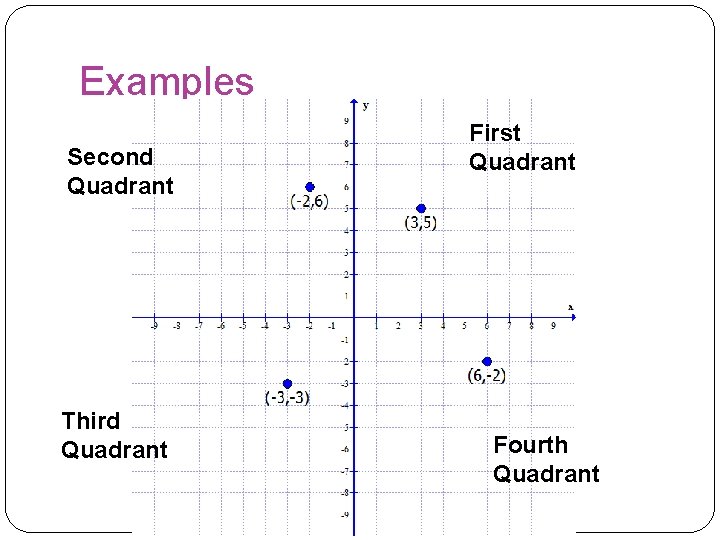
Examples Second Quadrant Third Quadrant First Quadrant Fourth Quadrant

Relation The concept of RELATION revolves around the concept of correspondence or association. Let's look at these examples Every day is associated with the maximum and minimum temperature. Every item in the supermarket is associated with a price. Each person who works has a monthly salary.

Relation A relation associates two quantities Note that the above examples show an association between two quantities. It is extremely important to establish associations between different types of phenomena, since once the correspondence is known, you can make predictions.

Definition of relation A relation consists of two sets and a rule of correspondence, such that to each element of the first set corresponds one or more elements in the second set. The first set is known as the domain and the second set is called the range.

Example 1 Consider a supermarket. You can find thousands of products. A possible relationship is to assign each product its price. The domain consists of the set of all the products sold by the supermarket. The range is the set of positive numbers, in symbols, the interval (0, ∞).

Example We can use the variable P to identify the different products that are in the supermarket. This variable is the independent variable. The set of all products is the domain. We can use the variable C to represent the cost of the product, that is, the price. This is the dependent variable The set of all possible prices is the range.

Example 2 Consider the following situation: Students enrolled in this course. A possible relationship is to associate with each person their student number. The Domain consists of the names of the students and the range is the set of student numbers.

Summary The relationships we will study in this course are those that the domain is a set of numbers and the range is also a set of numbers. Most of the phenomena studied in the Natural Sciences and in Business Administration are relations.

Definiton of relation Another way to define a relation is as a set of ordered pairs. In the ordered pair the first coordinate represents an element of the domain and the second coordinate represents a number of the range. We use the variable x to represent an element of the domain and y to represent an element of the range.

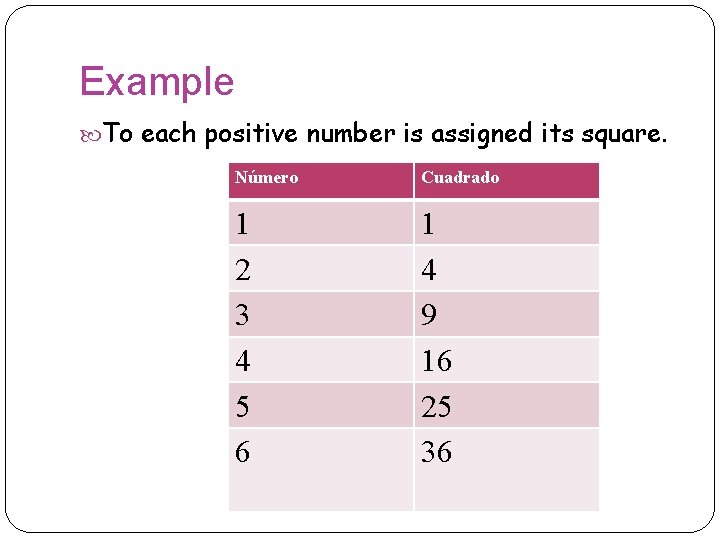
Example To each positive number is assigned its square. Número Cuadrado 1 2 3 4 5 6 1 4 9 16 25 36

Relation Each time we establish a relationship, ordered pairs are formed. In the previous example we have: Relation: {(1, 1), (2, 4), (3, 9), (4, 16), (5, 25), (6, 36)} Domain { 1, 2, 3, 4, 5, 6 } Range: {1, 4, 9, 16, 25, 36 }

Summary A relation is a set of ordered pairs The first coordinate of the ordered pair represents an element of the domain and the second coordinate represents a range element. Usually, we use the variable x to represent an element of the domain. To represent a scope element we use y. A relation can be represented by an equation

Graphs What is a graph? It is the geometric representation of the set of points that satisfies an equation. Method for graphing a Linear Equation: Arbitrarily select some numbers from the domain Substitute in the equation to find the value of y Draw the ordered pairs and join them

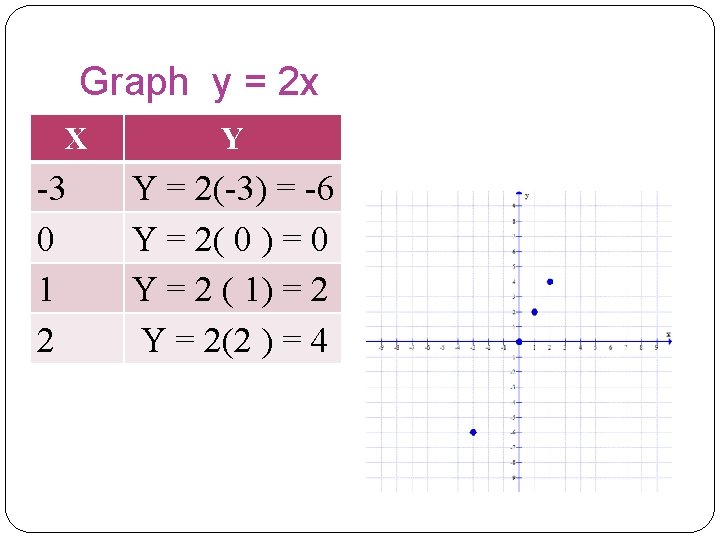
Graph y = 2 x X -3 0 1 2 Y Y = 2(-3) = -6 Y = 2( 0 ) = 0 Y = 2 ( 1) = 2 Y = 2(2 ) = 4

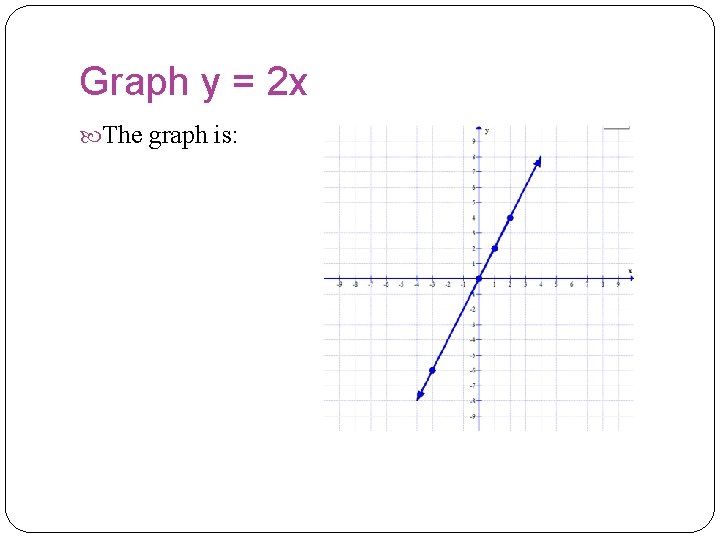
Graph y = 2 x The graph is:

Graph Y = 3 x -2 Y = - 4 x + 1

Intercepts Algebraically, an x-intercept is a point on the graph where y is zero, and. a y-intercept is a point on the graph where x is zero. Geometrically, the x-intercepts are where the graph crosses the x-axis, and the y-intercepts are where the graph crosses the y-axis.

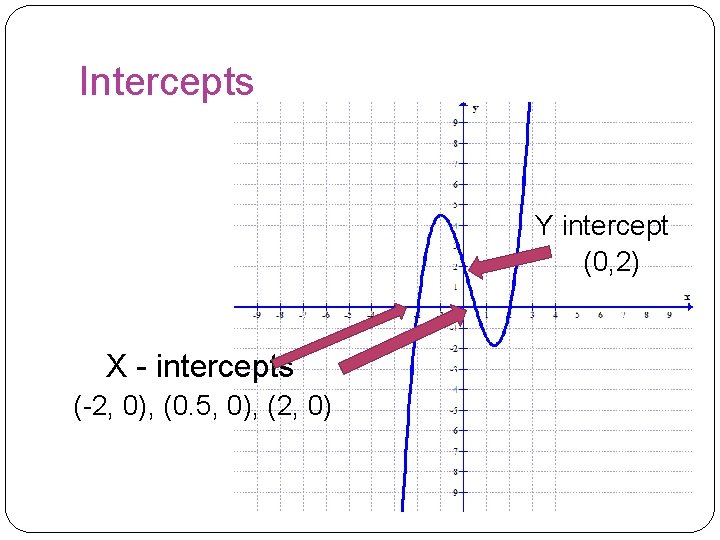
Intercepts Y intercept (0, 2) X - intercepts (-2, 0), (0. 5, 0), (2, 0)

Graphing a linear equation using the intercepts Find the x- and y – intercepts ( provided they are not the origin) and draw a line through them.

Example: Graph Y = 2 x - 6 Find the x- intercept Solve 0 = 2 x - 6 6 = 2 x 3 = x, (3, 0) is the x - intercept Find the y – intercept Solve Y = 2(0) - 6 Y = 6 , (0, - 6) is the y - intercept

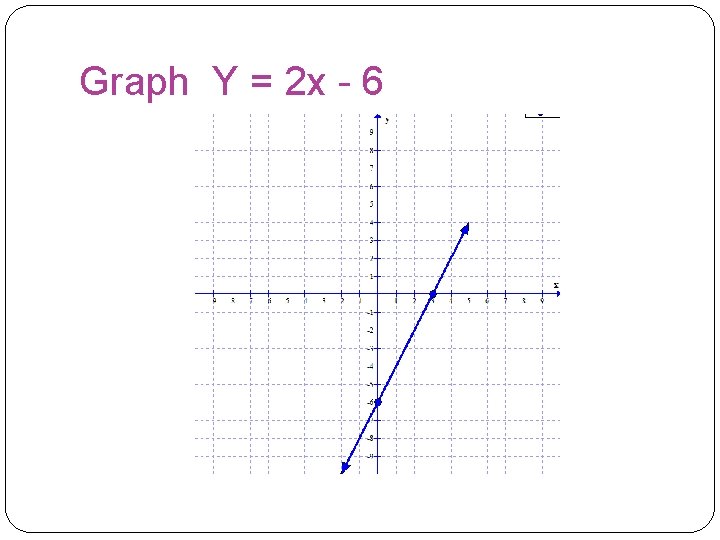
Graph Y = 2 x - 6

Linear inequalities

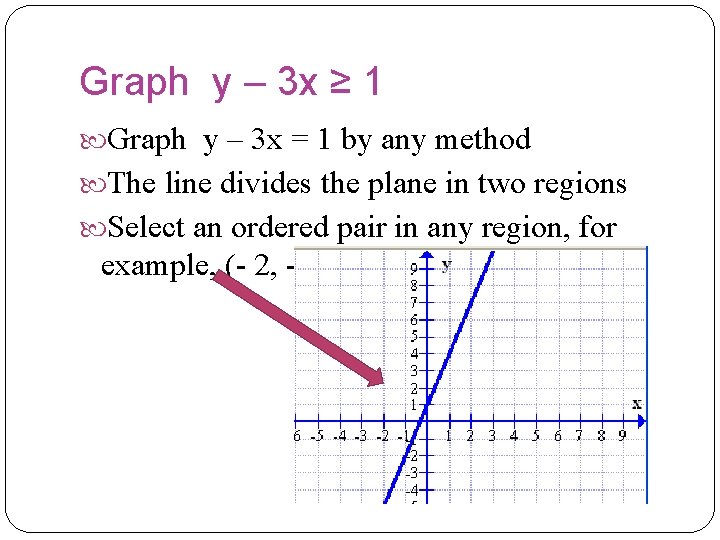
Graph y – 3 x ≥ 1 Graph y – 3 x = 1 by any method The line divides the plane in two regions Select an ordered pair in any region, for example, (- 2, - 2)

Linear inequalities Replace this pair ( -2, -2) in the inequality -2 – 3(-2) ≥ 1 -2 + 6 ≥ 1 4 ≥ 1 True Since this inequality is true and the pair we selected was to the left of the line we have to shade everything to the left of the line

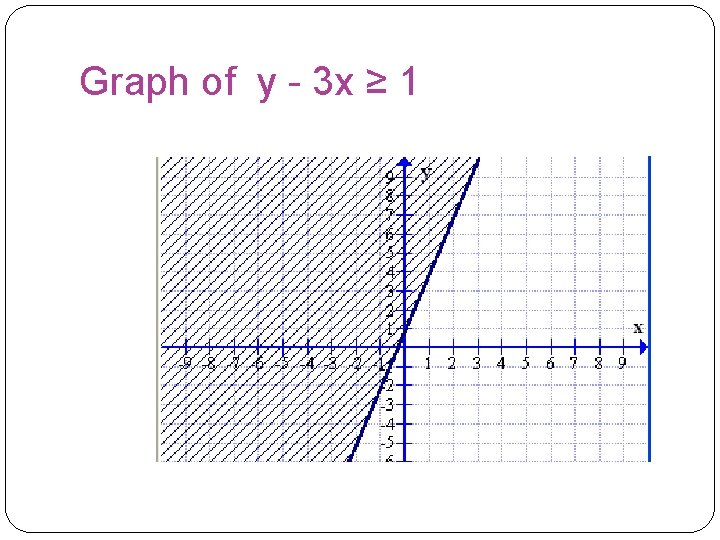
Graph of y - 3 x ≥ 1

Distance between 2 points We need a formula to calculate the distance between two points in the Cartesian plane.

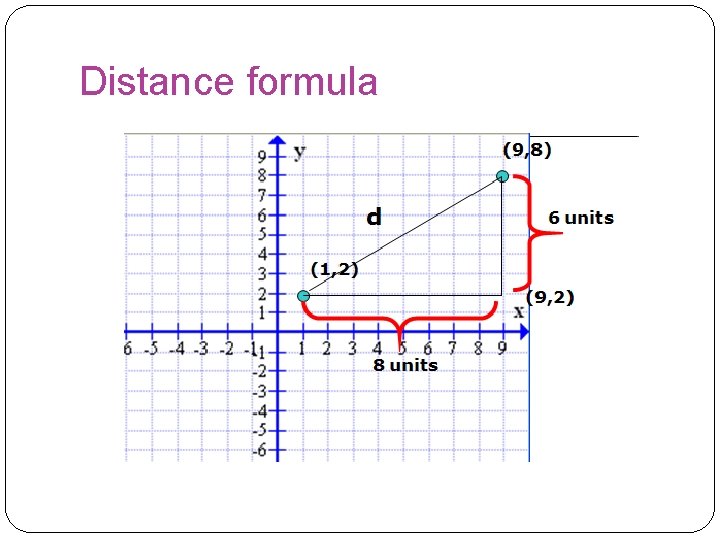
Distance formula

Distance formula We want to find d. Note that a right triangle was formed and the Pythagorean theorem is satisfied: c 2 = a 2 + b 2 In our case d is replaced by the letter c, a represents the length (9 - 1) = 8 and b represents the length of the other side (8 - 2) = 6. Therefore,

Exercises Find the distance between: (-1, 2) and (3, 5) (4, 7) y (-2, -5)

Midpoint Formula Sometimes you need to find the point that is exactly midway between two other points. For instance, you might need to find a line that divides into two equal halves a given line segment. This middle point is called the midpoint.

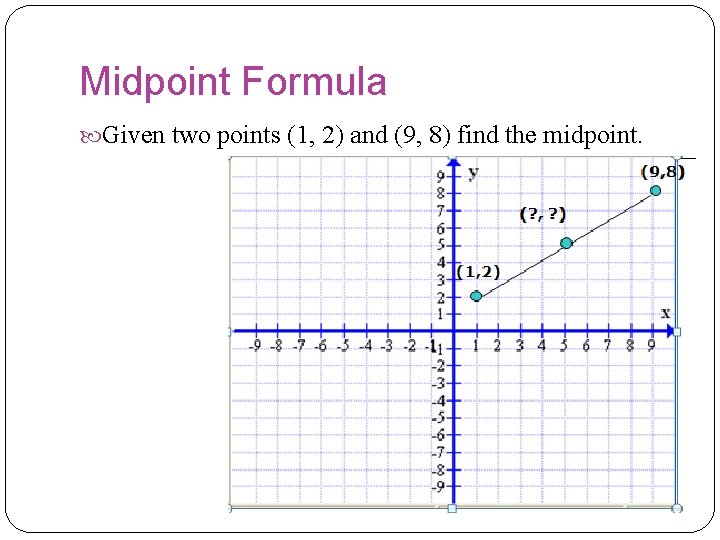
Midpoint Formula Given two points (1, 2) and (9, 8) find the midpoint.

Midpoint Formula The formula is In our example :

Exercise Find the midpoint between (0, -3) and ( - 4, 9)

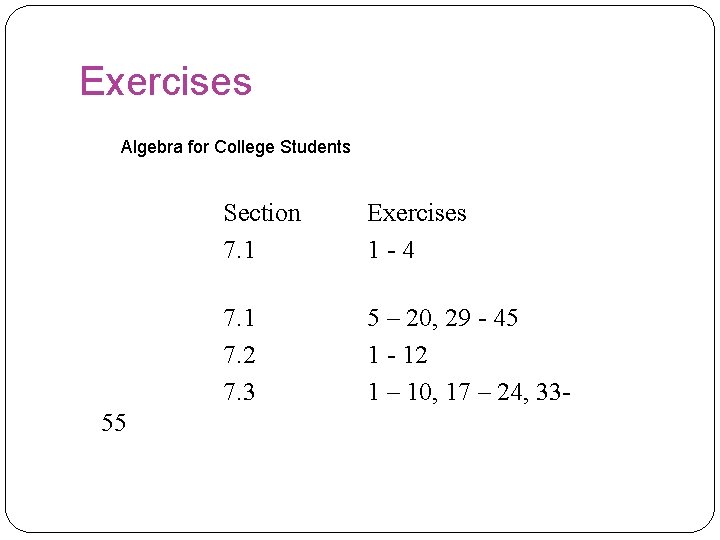
Exercises Algebra for College Students 55 Section 7. 1 Exercises 1 -4 7. 1 7. 2 7. 3 5 – 20, 29 - 45 1 - 12 1 – 10, 17 – 24, 33 -