Relations and Digraphs Contents 1 Relations and Directed

Relations and Digraphs

Contents 1. Relations and Directed Graphs 2. Special Properties of Binary Relations 3. Equivalence Relations 4. Ordering Relations, Lattices, Enumeration 5. Operations on relations

Introduction • Applications of relations are found throughout computer science and engineering, including relations between the inputs and outputs of computer programs, relations between data attributes in databases, and relations between symbols in computer languages.

Representing Relations using Digraphs Def 1. A directed graph (digraph) consists of a set V of vertices (or nodes) together with a set E of ordered pairs of elements of V called edges (or arcs). Example. Show the digraph of the relation R={(1, 1), (1, 3), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (4, 1)} on the set {1, 2, 3, 4}. Sol : 1 vertex : 1, 2, 3, 4 edge : (1, 1), (1, 3), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), 4 Ch 8 -4 (4, 1) 2 3

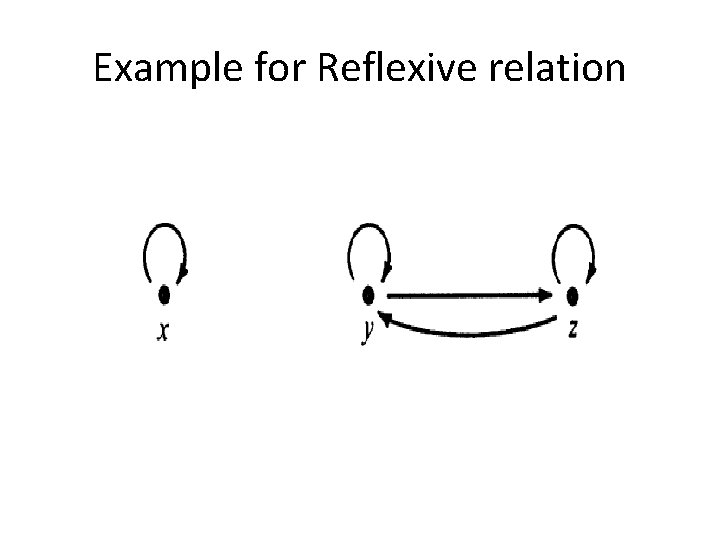
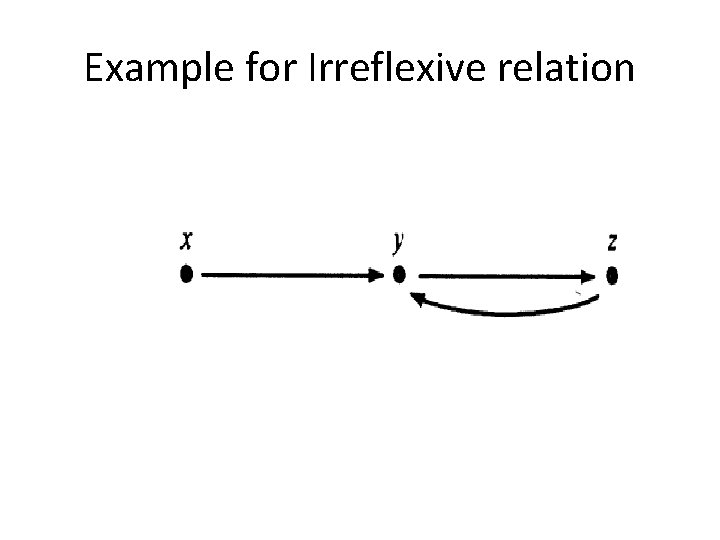
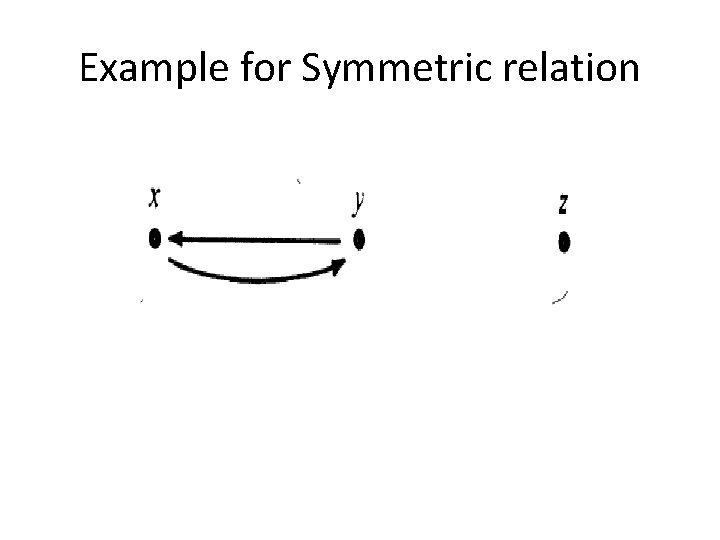
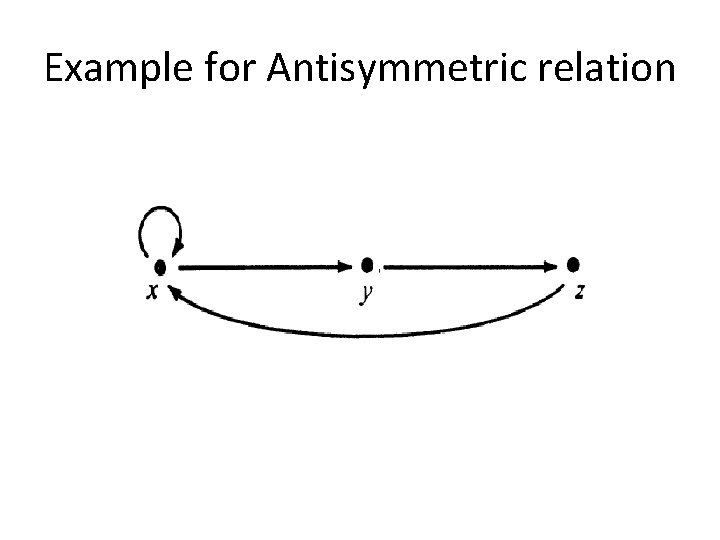
※ The relation R is reflexive iff for every vertex, (loop) ※ The relation R is symmetric iff for any vertices x≠y, either x y or x y ※ The relation R is antisymmetric iff for any x≠y, x y or x y Ch 8 -5

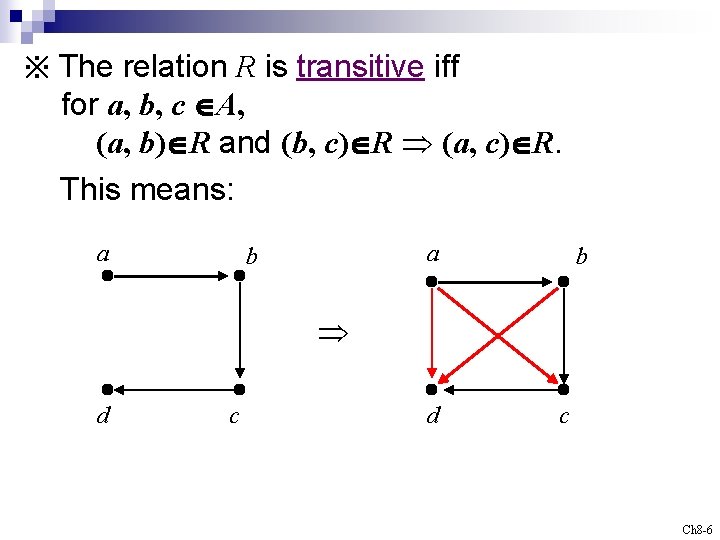
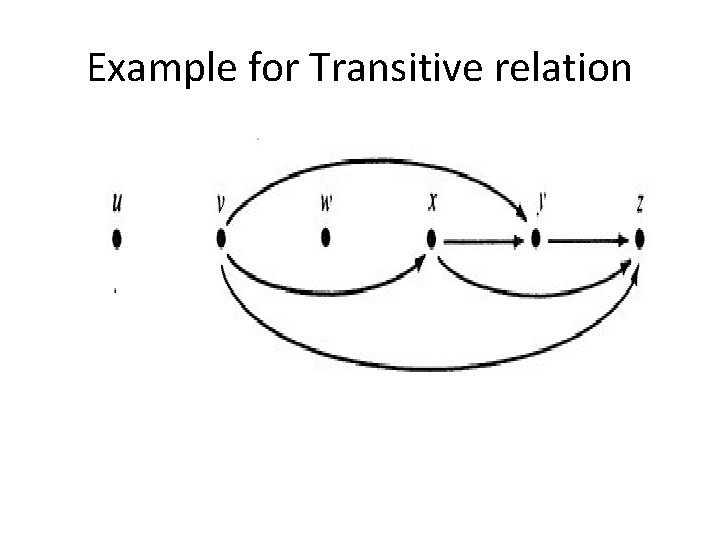
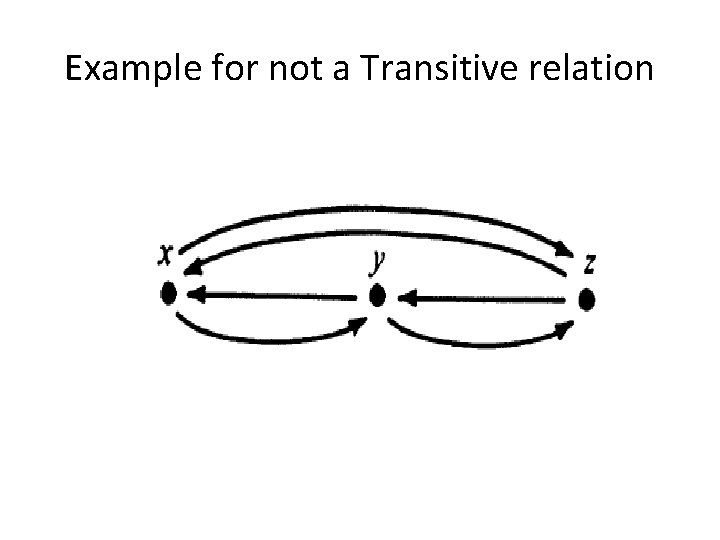
※ The relation R is transitive iff for a, b, c A, (a, b) R and (b, c) R (a, c) R. This means: a a b b d c Ch 8 -6

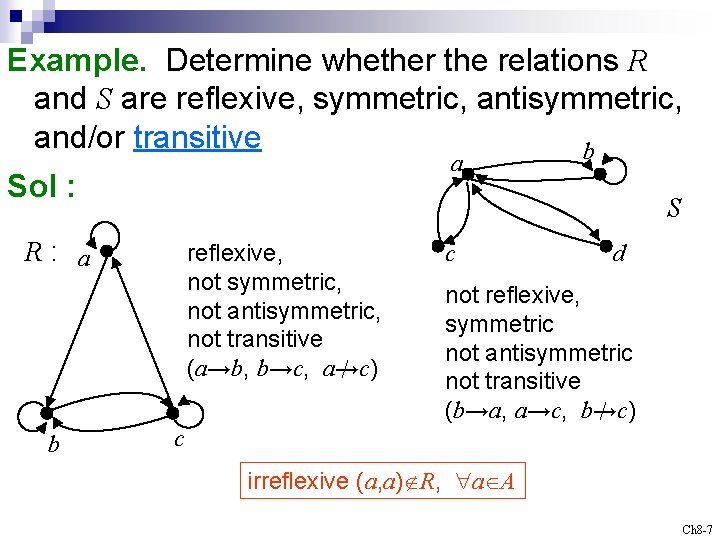
Example. Determine whether the relations R and S are reflexive, symmetric, antisymmetric, and/or transitive b a Sol : S R: a b reflexive, not symmetric, not antisymmetric, not transitive (a→b, b→c, a→c) c d not reflexive, symmetric not antisymmetric not transitive (b→a, a→c, b→c) c irreflexive (a, a) R, a A Ch 8 -7

Equivalence Relations Def 1. A relation R on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive. Example 1. Let R be the relation on the set of integers such that a. Rb if and only if a=b or a=-b. Then R is an equivalence relation. Example 2. Let R be the relation on the set of real numbers such that a. Rb if and only if a-b is an integer. Then R is an equivalence relation. Ch 8 -8

Example. (Congruence Modulo m) Let m Z and m > 1. Show that the relation R={ (a, b) | a≡b (mod m) } is an equivalence relation on the set of integers. ( a is congruent to b modulo m) Sol : Note that a≡b(mod m) iff m | (a-b). ∵ a≡a (mod m) (a, a) R reflexive If a≡b(mod m), then a-b=km, k Z b-a= (-k)m b≡a (mod m) symmetric If a≡b(mod m), b≡c(mod m) then a-b=km, b-c=lm a-c=(k+l)m a≡c(mod m) transitive ∴ R is an equivalence relation.

Example. Let l(x) denote the length of the string x. Suppose that the relation R={(a, b) | l(a)=l(b), a, b are strings of English letters } Is R an equivalence relation? Sol : (a, a) R string a (a, b) R (b, a) R reflexive symmetric Yes. (a, b) R, (b, c) R (a, c) R transitive Ch 8 -10

Example. Let R be the relation on the set of real numbers such that x. Ry if and only if x and y differ by less than 1, that is |x- y| < 1. Show that R is not an equivalence relation. Sol : x. Rx x since x- x =0 reflexive x. Ry |x- y| < 1 |y- x| < 1 y. Rx symmetric x. Ry, y. Rz |x- y| < 1, |y- z| < 1 |x- z| < 1 Not transitive Ch 8 -11

Representing Relations using Digraphs Def 1. A directed graph (digraph) consists of a set V of vertices (or nodes) together with a set E of ordered pairs of elements of V called edges (or arcs). Ch 8 -12

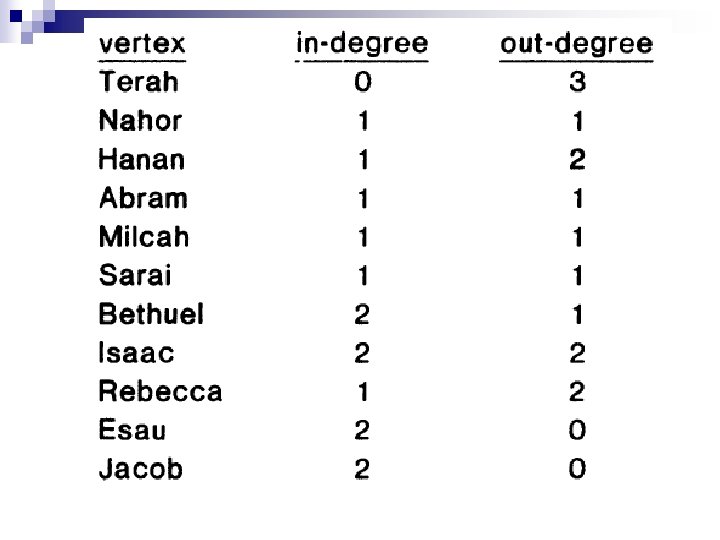
DIGRAPH • A pair of sets G = (V, E) is a directed graph (digraph) if. The elements of V are called vertices and the elements of E are called edges. • An edge (x, y) is said to be from x to y, and is represented in a diagram by an arrow with the tail at x and the head at y. Such an edge is said to be incident from x, incident to y, and incident on both x and y. • If there is an edge in E from x to y we say x is adjacent to y. The number of edges incident from a vertex is called the out-degree of the vertex and the number of edges incident to a vertex is called the in-degree. • An edge from a vertex to itself is called a loop, and will ordinarily be permitted. A digraph with no loops is called loop-free or simple.

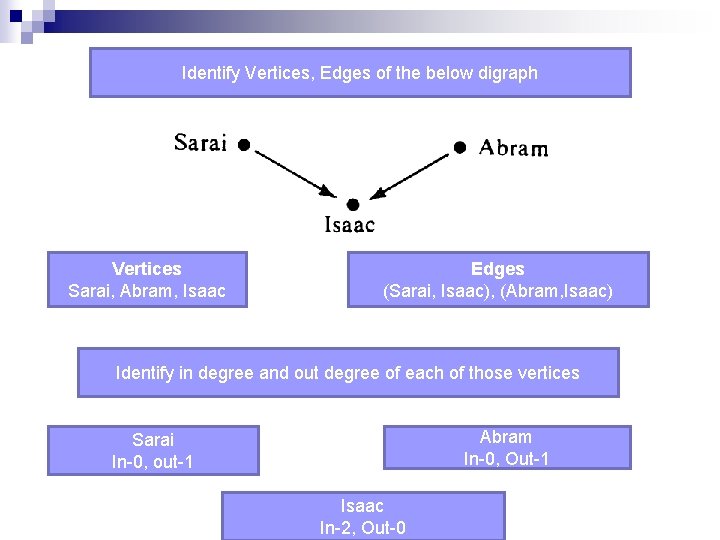
Identify Vertices, Edges of the below digraph Vertices Sarai, Abram, Isaac Edges (Sarai, Isaac), (Abram, Isaac) Identify in degree and out degree of each of those vertices Abram In-0, Out-1 Sarai In-0, out-1 Isaac In-2, Out-0

n Out-degree – the number of edges incident from a vertex n In-degree – the number of edges incident to a vertex n Loop-free (or) simple digraph – a digraph with no loops

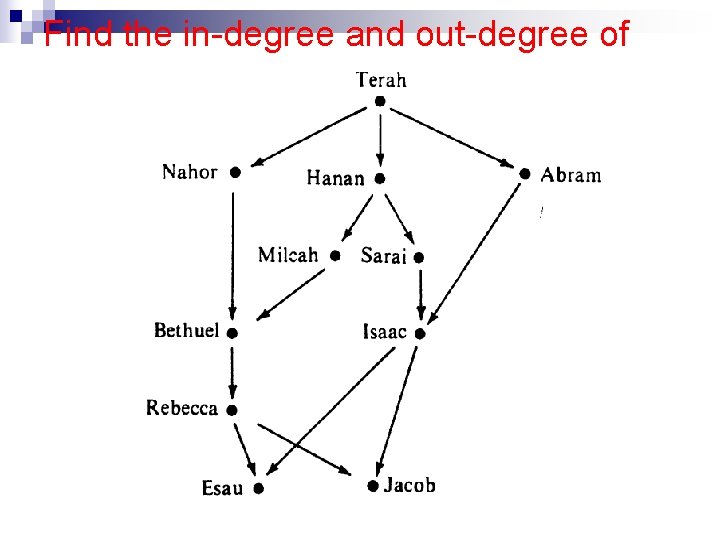
Find the in-degree and out-degree of

Paths in Directed Graphs Def 1. A path from a to b in the digraph G is a sequence of edges (x 0, x 1), (x 1, x 2), …, (xn-1, xn) in G, where n Z+, and x 0= a, xn= b. This path is denoted by x 0, x 1, x 2, …, xn and has length n. Ex. 1 2 3 4 5 A path from 1 to 5 of length 4 Theorem 1 Let R be a relation on a set A. There is a path of length n, where n Z+, from a to b if and only if (a, b) Rn. Ch 8 -18

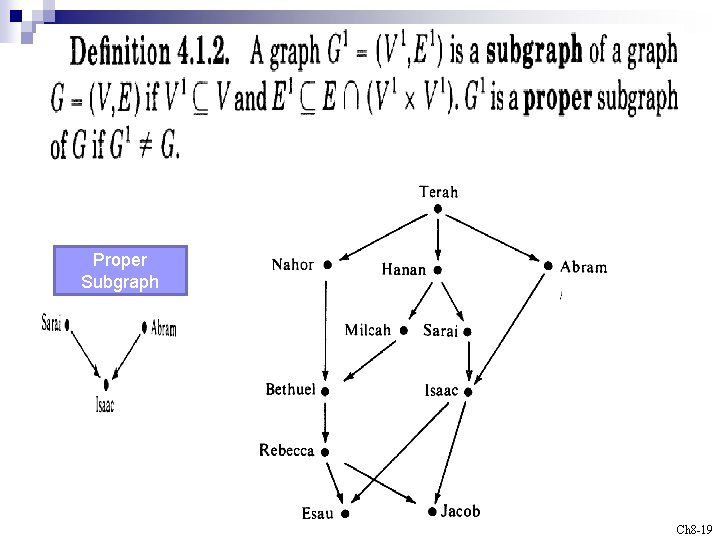
Proper Subgraph Ch 8 -19

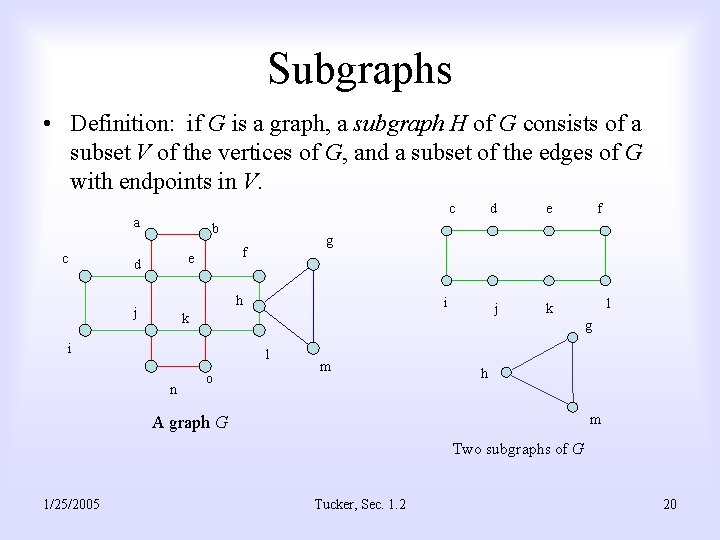
Subgraphs • Definition: if G is a graph, a subgraph H of G consists of a subset V of the vertices of G, and a subset of the edges of G with endpoints in V. c a c b h j i k j k f l g i l n e g f e d d o m h m A graph G Two subgraphs of G 1/25/2005 Tucker, Sec. 1. 2 20

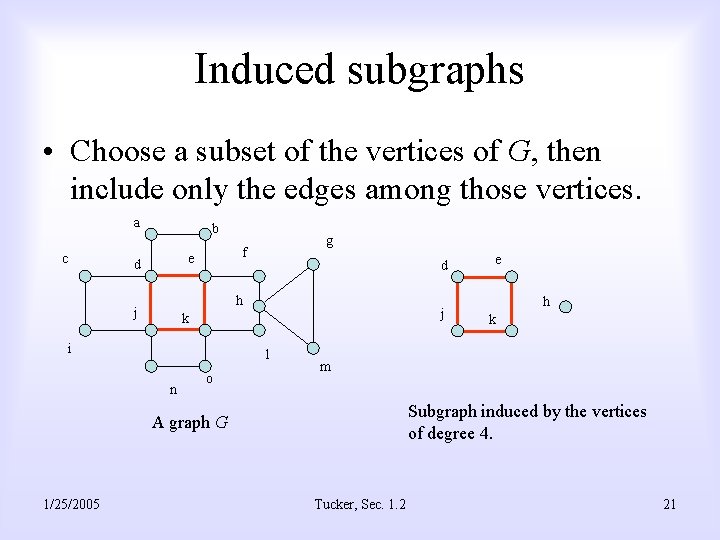
Induced subgraphs • Choose a subset of the vertices of G, then include only the edges among those vertices. a c b e d g f d h j j k i l n o h k m Subgraph induced by the vertices of degree 4. A graph G 1/25/2005 e Tucker, Sec. 1. 2 21

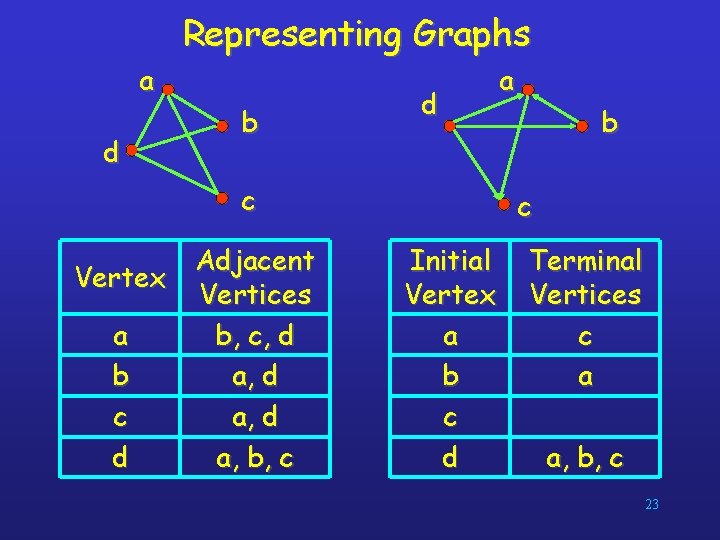
Representing Graphs a d b d c Adjacent Vertex Vertices a b, c, d b a, d c a, d d a, b, c a b c Initial Vertex a b c d Terminal Vertices c a a, b, c 23

Definition of Isomorphism • Two graphs G and are isomorphic if : – There exists a one-to-one correspondence between vertices in G and , such that – There is an edge between a and b in G if and only if there is an edge between the corresponding vertices and in. • The definition for oriented graphs is the same, except the head and tail of each edge of G must correspond to the head and tail in 1/25/2005 Tucker, Sec. 1. 2 . 24

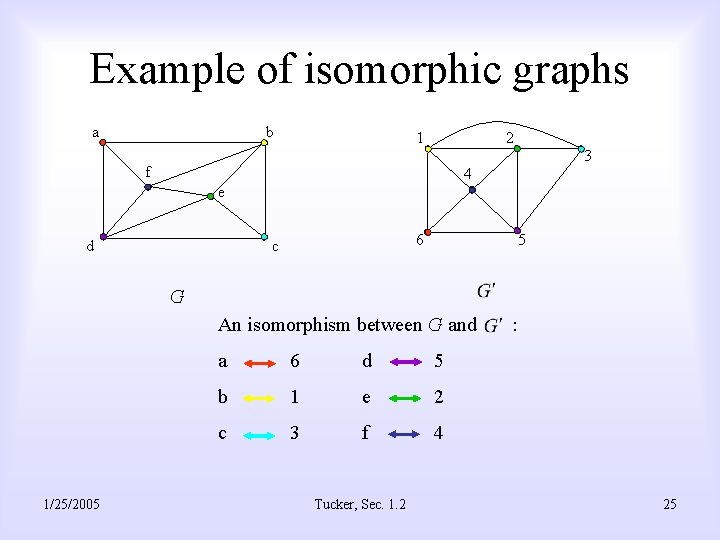
Example of isomorphic graphs a b 1 2 3 f 4 e d 6 c 5 G An isomorphism between G and 1/25/2005 a 6 d 5 b 1 e 2 c 3 f 4 Tucker, Sec. 1. 2 : 25

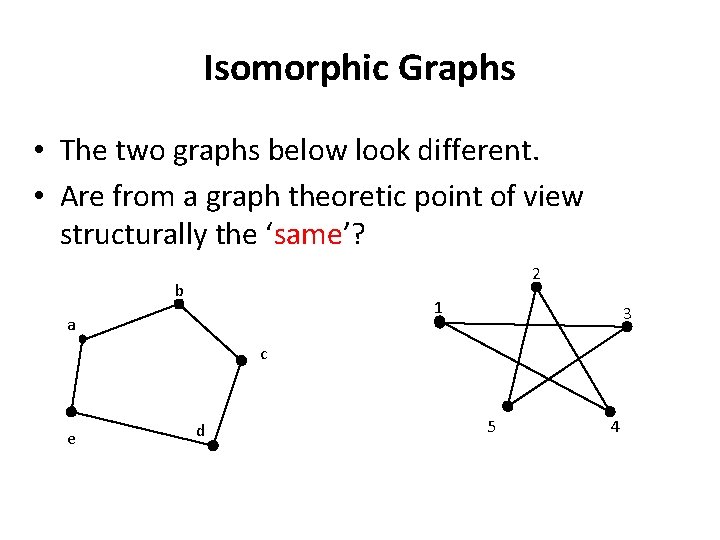
Isomorphic Graphs • The two graphs below look different. • Are from a graph theoretic point of view structurally the ‘same’? 2 b 1 a 3 c e d 5 4

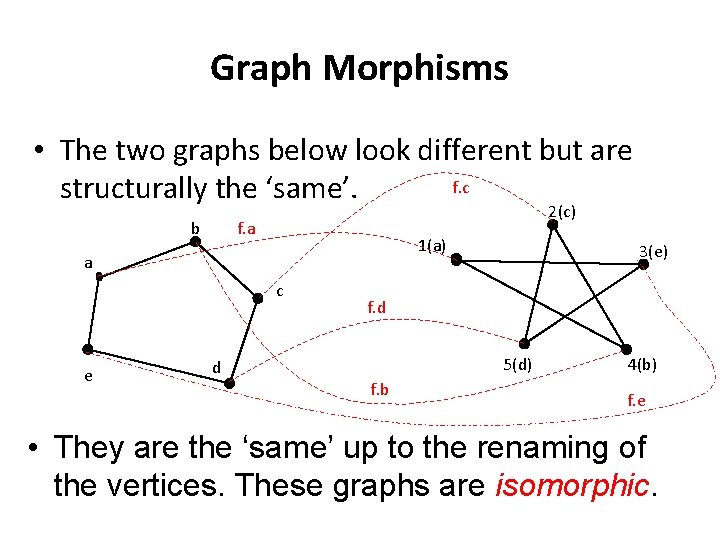
Graph Morphisms • The two graphs below look different but are f. c structurally the ‘same’. b 2(c) f. a 1(a) a c e 3(e) f. d 5(d) d f. b 4(b) f. e • They are the ‘same’ up to the renaming of the vertices. These graphs are isomorphic.

Elementary properties of isomorphic graphs • Edge and vertex counts – Isomorphic graphs have the same number of edges and vertices. • Vertex sequence (the list of vertex degrees) – Isomorphic graphs have the same vertex sequences. • Warning!! These can be used to show two graphs are not isomorphic, but can not show that two graphs are isomorphic. 1/25/2005 Tucker, Sec. 1. 2 28

Two non-isomorphic graphs Vertices: 6 Edges: 7 Vertex sequence: 4, 3, 3, 2, 2, 0. 1/25/2005 Vertices: 6 Edges: 7 Vertex sequence: 5, 3, 2, 2, 1, 1. Tucker, Sec. 1. 2 29

Subgraph properties of isomorphic graphs • Isomorphic graphs have the same sets of subgraphs: – there is a one-to-one correspondence between the subgraphs such that corresponding subgraphs are isomorphic. • Typically check induced subgraphs, or number of a specific kind of subgraphs such as cycles or cliques. • Warning!! These can be used to show two graphs are not isomorphic, but can not show that two graphs are isomorphic. 1/25/2005 Tucker, Sec. 1. 2 30

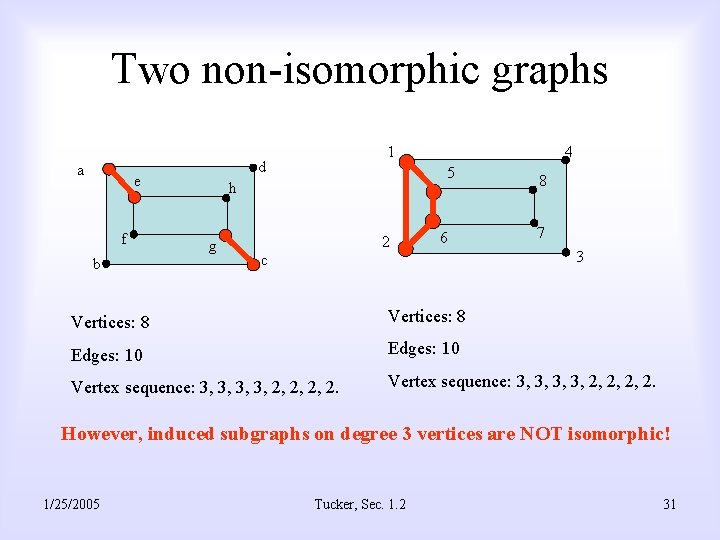
Two non-isomorphic graphs a d e f b 1 5 h g 4 2 6 c 8 7 3 3 Vertices: 8 Edges: 10 Vertex sequence: 3, 3, 2, 2, 2, 2. However, induced subgraphs on degree 3 vertices are NOT isomorphic! 1/25/2005 Tucker, Sec. 1. 2 31

An approach to checking isomorphism: ü Count the vertices. The graphs must have an equal number. ü Count the edges. The graphs must have an equal number. ü Check vertex degree sequence. Each graph must have the same degree sequence. ü Check induced subgraphs for isomorphism. If the subgraphs are not isomorphic, then the larger graphs are not either. üCount numbers of cycles/cliques. If these tests don’t help, and you suspect the graphs actually are isomorphic, then try to find a one-to-one correspondence between vertices of one graph and vertices of the other. Remember that a vertex of degree n in the one graph must correspond to a vertex of degree n in the other. 1/25/2005 Tucker, Sec. 1. 2 32

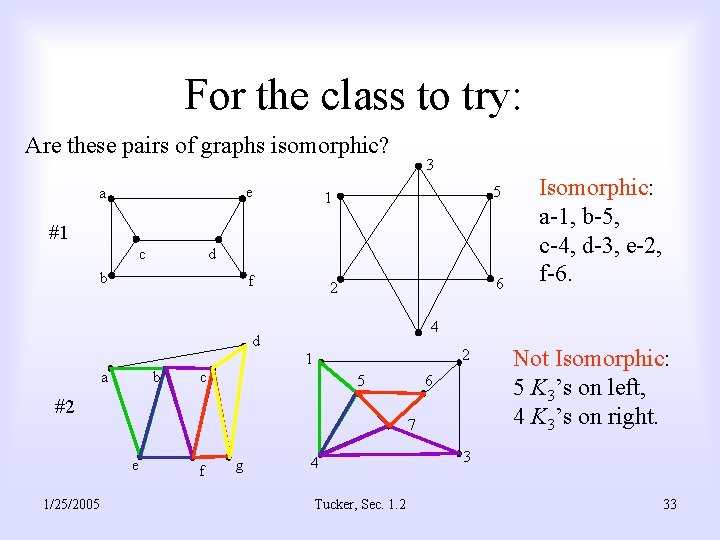
For the class to try: Are these pairs of graphs isomorphic? e a 3 5 1 #1 c d b f d a b 6 2 4 2 1 c 5 #2 1/25/2005 6 7 e f g Isomorphic: a-1, b-5, c-4, d-3, e-2, f-6. 4 Tucker, Sec. 1. 2 Not Isomorphic: 5 K 3’s on left, 4 K 3’s on right. 3 33

Problems

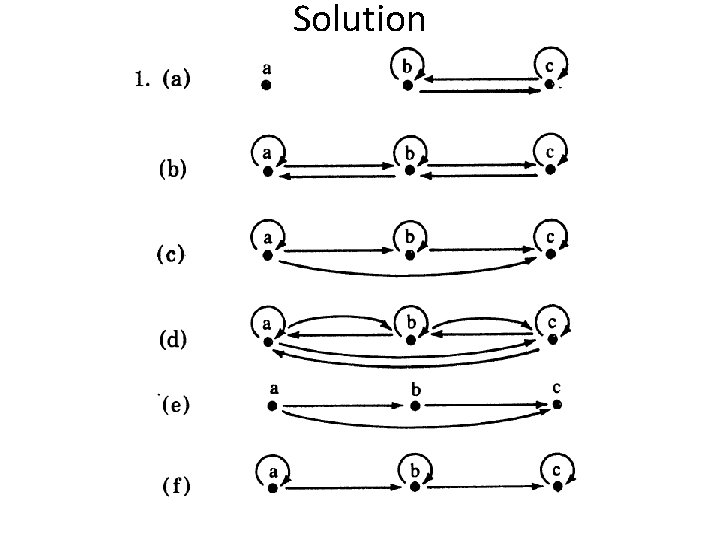
Solution for 1(a)

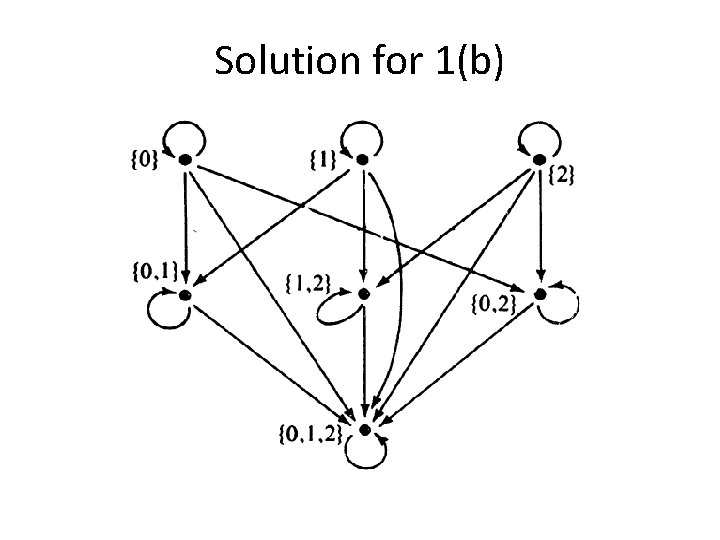
Solution for 1(b)

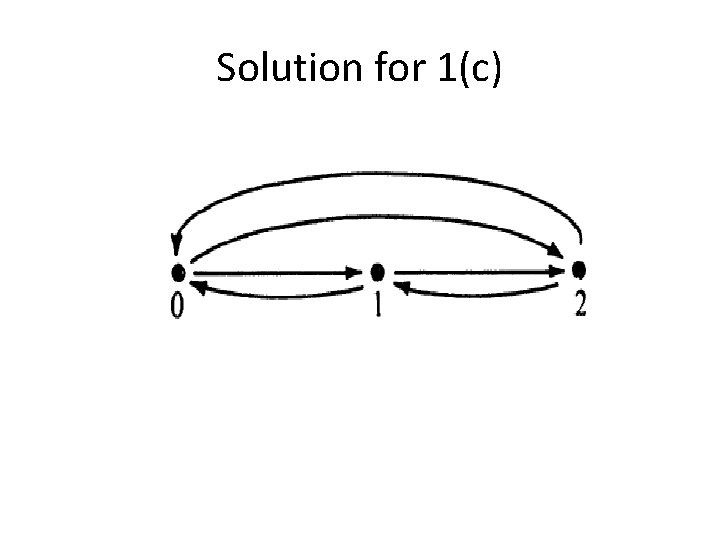
Solution for 1(c)

Example for Transitive relation

Example for not a Transitive relation

Example for Reflexive relation

Example for Irreflexive relation

Example for Symmetric relation

Example for Antisymmetric relation

• Equivalence relation – A binary relation that is transitive, reflexive and symmetric is called an equivalence relation • Partial ordering relation – A binary relation that is transitive, reflexive and antisymmetric is called a partial ordering relation

Problem

Solution