Relational Query Languages Relational Algebra procedural Relational Calculus

Relational Query Languages Relational Algebra (procedural) Relational Calculus (non-procedural) 1

Relational Languages • Relational Algebra (procedural) – defines operations on tables • Relational Calculus (declarative) – based on first-order predicate calculus • Every relational algebra query can be translated to relational calculus • Every safe relational calculus query can be translated to relational algebra. • Any language that is atleast as expressive as relational algebra is said to be relationally complete.

Relational Algebra Operators • Select: given a relation R and a predicate P, select tuples from R that satisfy P. • Project: given a relation R and a subset of its attributes X, return a relation which is the same as R except that all columns not in X are left out. • Rename: given a relation R and a name N, return a relation that is exactly the same as R except that it has a name N. • Cartesian Product: Given 2 relations R 1 and R 2, . return a relation R 3 whose tuples are the concatenation of tuples in R 1 and R 2 • Union: Given relations R 1 and R 2, return a relation R 3 which contains all tuples in R 1 and R 2 • Set Difference: Given relations R 1 and R 2, return a relation R 3 containing all tuples in R 1 that are not in R 2 3
![Selection Operation • sselection cond(R) or select[selection cond]R • Example: Employee(name, dept, sal) select Selection Operation • sselection cond(R) or select[selection cond]R • Example: Employee(name, dept, sal) select](http://slidetodoc.com/presentation_image_h/2e923ab910e75ebce2d74b71ed432ae6/image-4.jpg)
Selection Operation • sselection cond(R) or select[selection cond]R • Example: Employee(name, dept, sal) select [sal > 20, 000] Employee sal name dept jane pharmacy 30, 000 jack hardware 30, 000 jill pharmacy 75, 000 joe toy 20, 000 bill toy 12, 000 jane jack jill pharmacy 30, 000 hardware 30, 000 pharmacy 75, 000 select [(dept = toy) or (sal < 20, 000)] Employee name joe bill dept toy sal 20, 000 12, 000 4
![Projection • Proj [list of attr of R] (R ) or P R A Projection • Proj [list of attr of R] (R ) or P R A](http://slidetodoc.com/presentation_image_h/2e923ab910e75ebce2d74b71ed432ae6/image-5.jpg)
Projection • Proj [list of attr of R] (R ) or P R A Jane Jim June B C Toy 10, 000 Toy 20, 000 Complaint 20, 000 Proj[A]R A Jane Jim June list of attr of R (R) S A C Jane Toy John Complaint Proj[CB]R C 10, 000 20, 000 B Toy Complaint Toy 5

Cartesian Product • Denoted by R x S R: A joe jack B toy com C 10 K 20 K S: A joe jack Rx. S: R. A joe jack B toy com C 10 K 20 K S. A joe jack D jill D jill attributes get the name, R. A, where A is attrib name, and R is the relation name from which attrib originates. If there is no possible ambiguity, relation name is dropped! • Notice attribute naming strategy to disambiguate attribute names 6

Set Difference • Denoted by R - S ( Illegal if R & S have different numbers of attributes or if respective domains mismatch!) R A B S Jane Toy Jim Toy June Complaint R-S= A Jim June A C Jane Toy John Complaint B Toy Complaint Note attributes in resulting relation take name from the first relation 7

Rename Operator • Strategy used to disambiguate attribute names: – For union and set difference operators, the resulting relation takes the attribute names of the first relation – For cartesian product, attributes are named as Relationname. attribute-name, where Relation name refers to the relation from which the attribute originally came. – Strategy will not disambiguate when the same relation appears multiple times in the relational query. • Let R(A, B) be a relation. Consider R x R the attributes of the resulting relation? • Define a rename operator: • denoted by rename[N]R or by r N(R) ---- what to name – returns a relation which is exactly same as R except it has the name N 8

Rename Operator • • Consider relation Employee(name, dept, sal) List all the employees who work in the same department as Jill We first find the department(s) for which Jill works – Proj[dept](select[name = Jill] Employee) ---list of departments for which Jill works To find out about all Employees working for this department, we need to reference the Employee table again: – select[P] ( Employee x Proj[dept](select[name = Jill] Employee) ) – where P is a selection predicate which requires dept values to be equal. If we use Employee. dept in P it is ambiguous which instance of Employee relation in the query the attribute refers to. To disambiguate, use rename operator: Proj[Employee. name](select[Employee. dept = Employee 2. dept] Employee x (Proj[dept] (select[name = Jill]( rename[Employee 2](Employee)))) 9

Formal Definition of Relational Algebra • Basic Expressions: – Relation in a database – Constant Relations • General Expressions: constructed from basic ones. Let E 1 and E 2 be relational algebra expressons. Then the following are also expressions: – E 1 U E 2, if arity of E 1 = E 2 and corresponding attributes are of the same type – E 1 - E 2, if arity of E 1 = E 2 and corresponding attributes are of the same type – E 1 x E 2, if attributes in E 1 and E 2 have different names – Select[P](E 1), where P is a predicate on attributes in E 1 – Proj[S](E 1), where S is a list of some attributes in E 1 – rename[X](E 1), where X is a new name for relation E 1 10

Additional Operators Basic Relational Algebra operators are like assembly language. Define more powerful operators that make the task of writing relational algebra queries easier Each of these operators can be expressed in relational algebra and do not increase the expressibility of the language Example: Intersection R Ç S = R - (R - S) = {t|t ÎR & t Î S} 11
![Joins R join condition S = select[ join condition] (R x S) join condition Joins R join condition S = select[ join condition] (R x S) join condition](http://slidetodoc.com/presentation_image_h/2e923ab910e75ebce2d74b71ed432ae6/image-12.jpg)
Joins R join condition S = select[ join condition] (R x S) join condition is of the form: <condition> AND <condition> where each condiition is of the form Ai q Bj, where – Ai is attribute of R – Bj is attribute of S – q is a comparison operator {=, <, >, <=, >=, <>} Example: E(emp, dept) M(dept, mgr) List all employees and their managers. Proj[emp, mgr](select[E. dept = M. dept] (Ex. M)) can be represented as: Proj[emp, mgr] ( E E. dept = M. dept M ) 12

Types of Joins • Theta-Join: if a join condition uses some comparison operator other than equality. – E. g. , list names of all managers who manage departments other than Jill’s – Proj[mgr]( select[emp = Jill](E ) (E. dept ¹ M. dept) M) • Equi-Join: if join conditions use only equality operator. – E. g. , list the manager’s name of Jill’s department – Proj[mgr]( select[emp = Jill](E ) (E. dept = M. dept) M) • Natural Join: special type of equi-join. . – Let R and S be relations. Let attributes of R and S be denoted by R and S respectively. – Denote by R U S the union of the list of attributes of R and S – Let list of attributes common to both R and S be {A 1, A 2, …, An} – Natural join of R and S (denoted R S) is: – Proj[R U S ] (R R. A 1 = S. A 1 and R. A 2 = S. A 2 and … and R. An = S. An S) – E. g. , Proj[mgr]( select[emp = Jill](E ) M) 13

Assignment Operator • Lots of time convenient to write relational algebra expressions in parts using assignment to temporary relational variables. • For this purpose use assignment operator, denoted by : = • E. g. , Who makes more than their manager? E(emp, dept, sal) M(mgr, dept) ESM(emp, sal, mgr) : = Proj[emp, sal, mgr] (E M) (Proj[ESM. emp](ESM [mgr = E. emp & ESM. sal >E. sal] E) ) • With the assignment operator, a query can be written as a sequential program consisting of a series of assignments followed by an expression whose value is the result of the query. 14

Examples • A query is a composition of basic relational algebra operators • Consider relations: – customer(ssno, name, street, city) – account(acctno, custid, balance) • list account balance of Sharad • list names of all customers who have a higher balance than all customers in Champaign
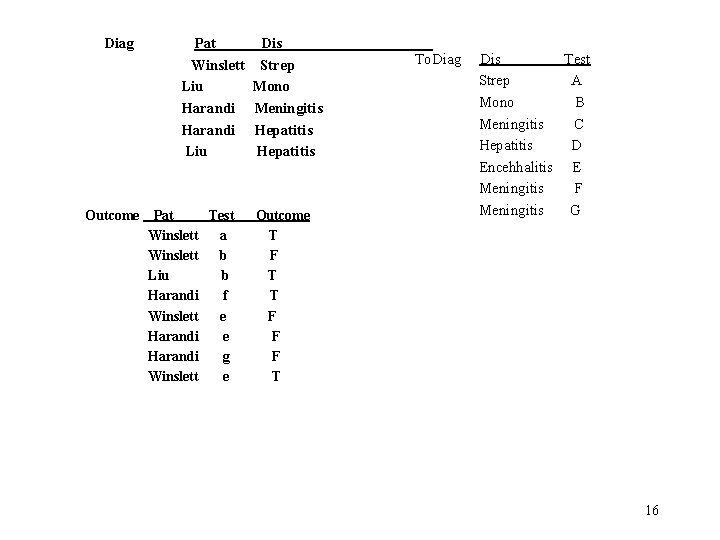
Diag Outcome Pat Winslett Liu Harandi Liu Pat Test Winslett a Winslett b Liu b Harandi f Winslett e Harandi g Winslett e Dis Strep Mono Meningitis Hepatitis Outcome T F T T F F F T To. Diag Dis Test Strep A Mono B Meningitis C Hepatitis D Encehhalitis E Meningitis F Meningitis G 16

1. Who has what disease? Diag 2. Who has a disease they have been tested for? – Proj[pat](Diag | | To. Diag | | Outcome) 3. Who has a disease they tested positively for? Proj[pat](Diag | | To. Diag | | (select[outcome = ‘T’])Outcome)) 4. Who has a disease that they tested both positively & negatively for? Temp 1(pat, dis) : = Proj[pat, dis](Diag | | To. Diag select[outcome = ‘T’])Outcome) Temp 2(pat, dis) : = Proj[pat, dis](Diag | | To. Diag select[outcome = ‘F’])Outcome) Proj[pat](Temp 1 Ç Temp 2) Use better names!! 17

Example of Queries in Relational Algebra 5. Who tested both positively and negatively for a disease, whether or not they have it? Testpos(pat, dis) = Proj[pat, dis](To. Diag | | select[outcome = ‘T’]) Outcome) Testneg(pat, dis) = Proj[pat, dis](To. Diag | | select[outcome = ‘F’]) Outcome) (Testpos Ç Testneg)[pat] 6. Who tested both positively & negatively for the same test? (Winslett) Proj[pat](Outcome | | condition (rename[Outcome 2](Outcome)) where condition is: [Outcome. pat = Outcome 2. pat & Outcome. test = Outcome 2. test & Outcome. outcome = Outcome 2. outcome] 18
![7. What testable disease does no one have? (encephalitis) Proj[dis]To. Diag - Proj[dis]Diag Note 7. What testable disease does no one have? (encephalitis) Proj[dis]To. Diag - Proj[dis]Diag Note](http://slidetodoc.com/presentation_image_h/2e923ab910e75ebce2d74b71ed432ae6/image-19.jpg)
7. What testable disease does no one have? (encephalitis) Proj[dis]To. Diag - Proj[dis]Diag Note technique: compute opposite of what you want, take a difference. Use in hard queries with negation (‘no one’) 8. What disease does more than one person have? Proj[dis](Diag condition rename[Diag 2](Diag)) where, condition is [Diag. pat ¹ Diag 2. pat & Diag. dis = Diag 2 dis] 9. What disease does everyone have? clue that query is very hard Disease(dis) : = diag[dis] Patients(pat) : = diag[pat] Diseases. Not. Everyone. Has(dis) : = Proj[dis]((Patients x Disease) Diag) Disease - Diseases Not Everyone Has Note technique used! A very hard query might require taking the difference several times. 19

Outer Joins E emp Jones Chu Swami Barth dept Missiles Tanks Revolver sal M 10 K 20 K 50 K 100 K mgr dept Mendez Tanks Frank Explosive Jones Missiles Right outer join of E with M emp Jones Chu null dept sal Missiles 10 K Tanks 20 K Explosives null mgr Jones Mendez Frank left outer join of E with M Full outer join of E with M emp dept sal Jones Missiles 10 K Chu Tanks 20 K Swami Tanks 50 K Barth Revolver 100 K null Explosives null mgr Jones Mendez null Frank emp dept sal Jones Missiles 10 K Chu Tanks 20 K Swami Tanks 50 K Barth Revolver 100 K mgr Jones Mendez null

Aggretate Functions • Mathematical aggregate functions (e. g. , sum, count, average, min, max) on a collection of values from the database. • [grouping attributes] F [function list] (<relation expression>) where grouping attributes specify how to group the tuples function list specify the aggregate functions to be applied to the individual groups relation expression is the expression that results in a relation. • Example: Consider a relation Employee(dno, ssno, sal). An expression [dno] F [COUNT ssno, AVERAGE salary] (Employee) results in a relation: dno #employee average_salary 1 10 10, 000 Queries involving aggregate functions cannot be expressed in 2 23 8000 pure relational algebra! 21

Recursive Closure Queries Consider parent relation parent Child sam Chuck Harvey Reggie Mom Anda Donna Betty Cristie Dad Chuck Harvey Reggie John It may be interesting to query the relation for the following: retrieve all the female anscestors of sam. retrieve all male ansestors of chuck retrieve harvey’s family tree retrieve all the descendants of cristie Such queries (in general) require an unbounded application of joins of the parent relation to itself and CANNOT be represented in relational algebra. 22
- Slides: 22