Relational Models CSE 515 in One Slide We








































- Slides: 57

Relational Models

CSE 515 in One Slide We will learn to: l Put probability distributions on everything l Learn them from data l Do inference with them

Beyond Vectors We want to put distributions on: l Trees l Graphs l Objects of different types and their relations l Class hierarchies l Relational databases l Knowledge bases l Programs l Etc.

Two Approaches l Piecemeal l l Develop probabilistic models for each All-in-one l l All are easily expressed in first-order logic Add probability to first-order logic

First-Order Logic l l l l Symbols: Constants, variables, functions, predicates E. g. : Anna, x, Mother. Of(x), Friends(x, y) Logical connectives: Conjunction, disjunction, negation, implication, quantification, etc. Literal: Atom (predicate) or its negation Clause: Disjunction of literals All formulas can be converted to conjunction of clauses Grounding: Replace all variables by constants E. g. : Friends (Anna, Bob) World: Assignment of truth values to all ground atoms

Example: Friends & Smokers

Example: Friends & Smokers

Example: Friends & Smokers

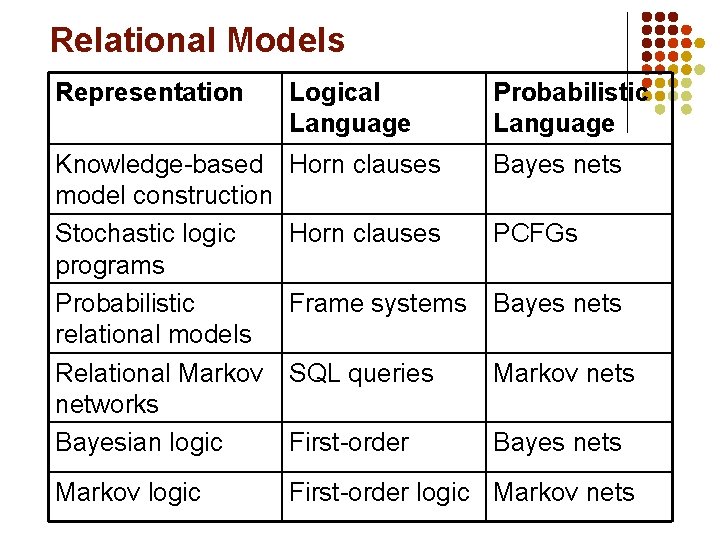
Relational Models Representation Logical Language Probabilistic Language Knowledge-based model construction Stochastic logic programs Probabilistic relational models Relational Markov networks Bayesian logic Horn clauses Bayes nets Horn clauses PCFGs Frame systems Bayes nets SQL queries Markov nets First-order Bayes nets Markov logic First-order logic Markov nets

Markov Logic l l l Most developed approach to date Many other approaches can be viewed as special cases Main focus of this lecture

Markov Logic: Intuition l l l A logical KB is a set of hard constraints on the set of possible worlds Let’s make them soft constraints: When a world violates a formula, It becomes less probable, not impossible Give each formula a weight (Higher weight Stronger constraint)

Markov Logic: Definition l A Markov Logic Network (MLN) is a set of pairs (F, w) where l l l F is a formula in first-order logic w is a real number Together with a set of constants, it defines a Markov network with l l One node for each grounding of each predicate in the MLN One feature for each grounding of each formula F in the MLN, with the corresponding weight w

Example: Friends & Smokers

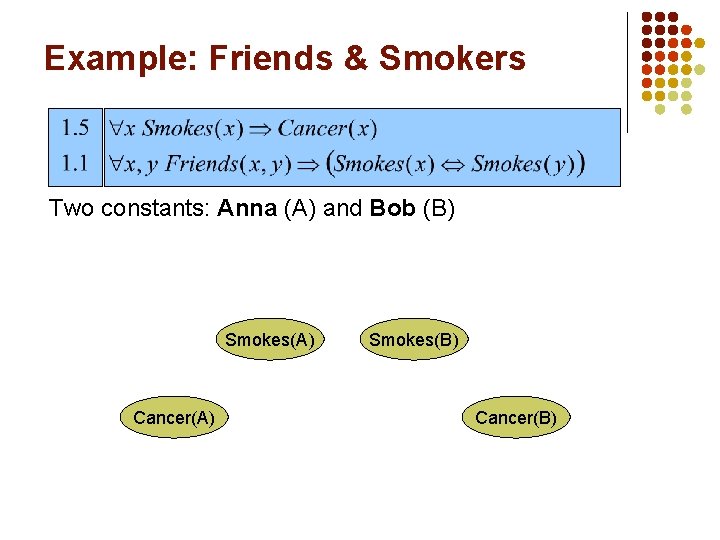
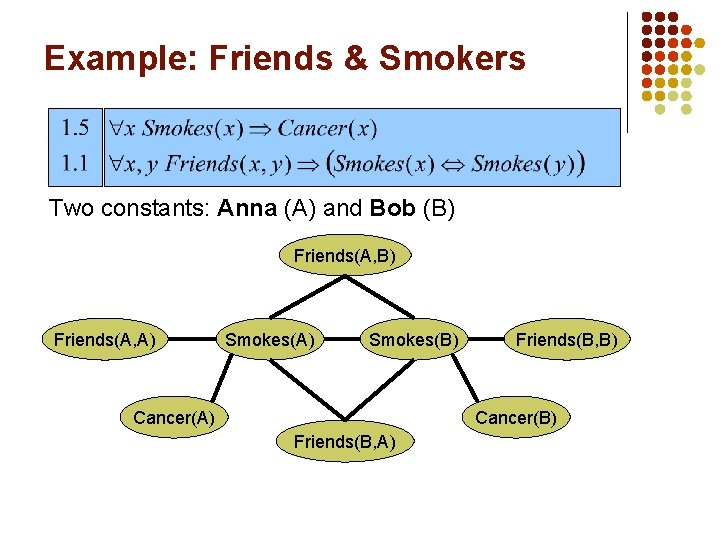
Example: Friends & Smokers Two constants: Anna (A) and Bob (B)

Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Smokes(A) Cancer(A) Smokes(B) Cancer(B)

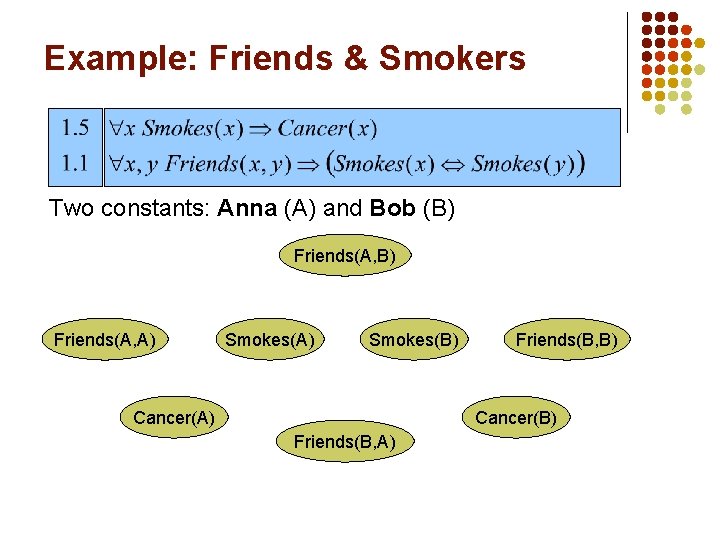
Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)

Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)

Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)

Markov Logic Networks l MLN is template for ground Markov nets l Probability of a world x: Weight of formula i l l l No. of true groundings of formula i in x Typed variables and constants greatly reduce size of ground Markov net Functions, existential quantifiers, etc. Infinite and continuous domains

Relation to Statistical Models l l l Markov logic has all the models we’ve seen in this class as special cases Markov logic allows objects to be interdependent (non-i. i. d. ) Markov logic makes it easy to compose models

Relation to First-Order Logic l l l Infinite weights First-order logic Satisfiable KB, positive weights Satisfying assignments = Modes of distribution Markov logic allows contradictions between formulas

Inference in Markov Logic l l P(Formula|MLN, C) = ? MCMC: Sample worlds, check formula holds P(Formula 1|Formula 2, MLN, C) = ? If Formula 2 = Conjunction of ground atoms l l First construct min subset of network necessary to answer query (generalization of KBMC) Then apply MCMC, belief propagation, etc.

Ground Network Construction network ← Ø queue ← query nodes repeat node ← front(queue) remove node from queue add node to network if node not in evidence then add neighbors(node) to queue until queue = Ø

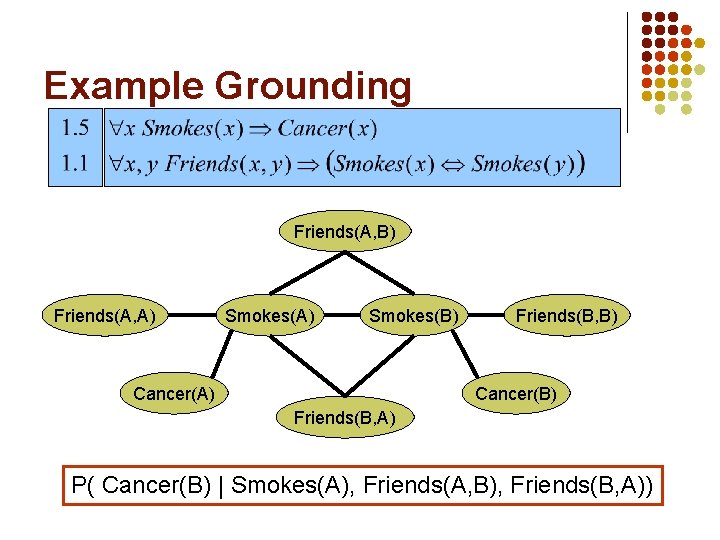
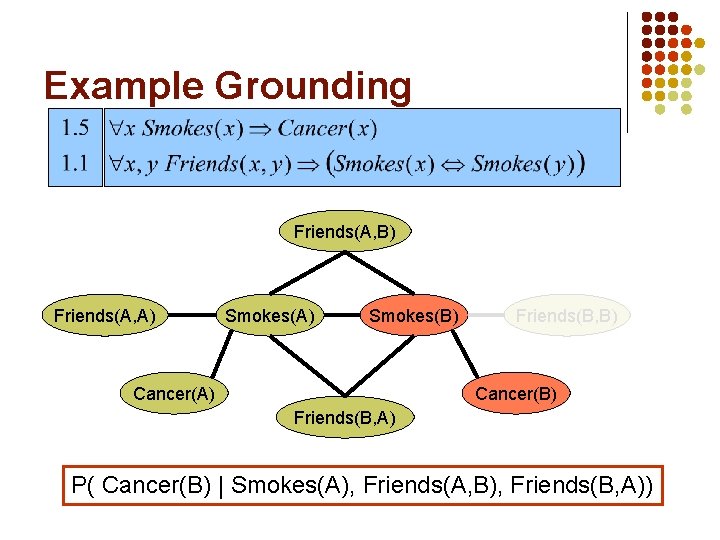
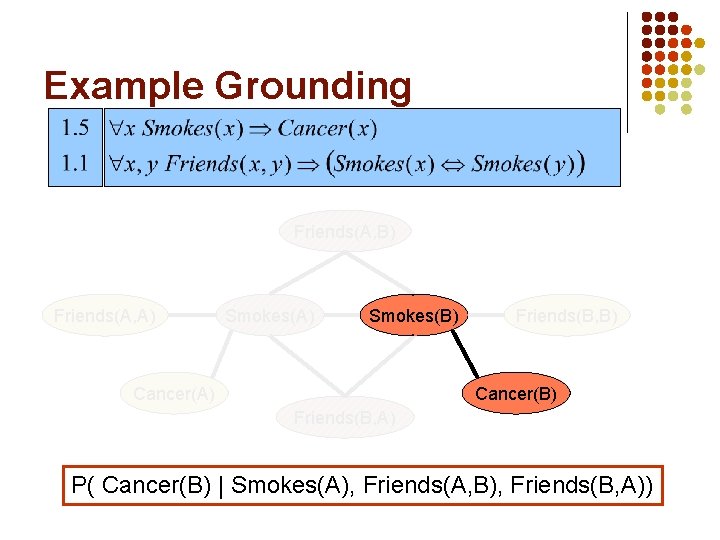
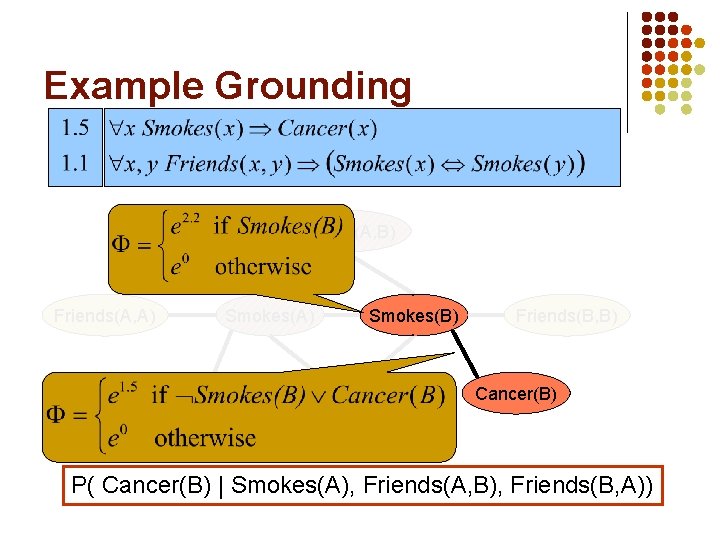
Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

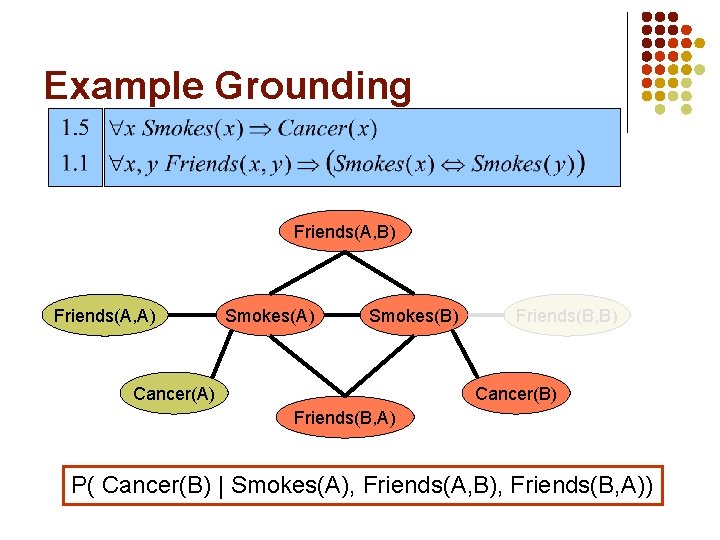
Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

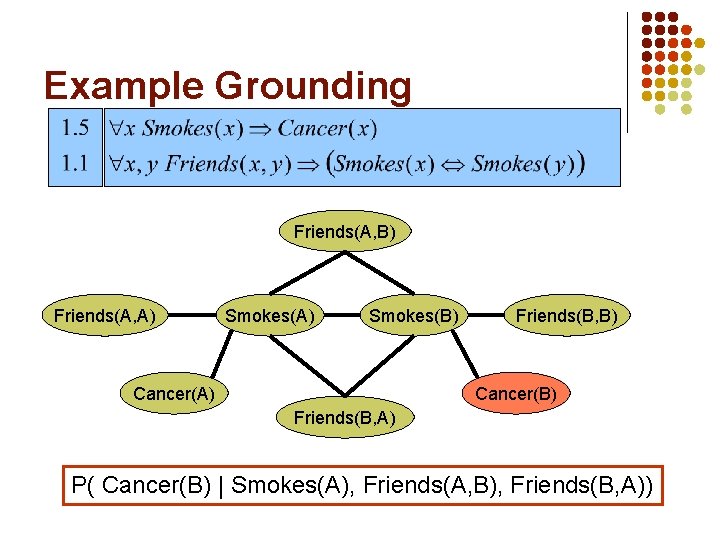
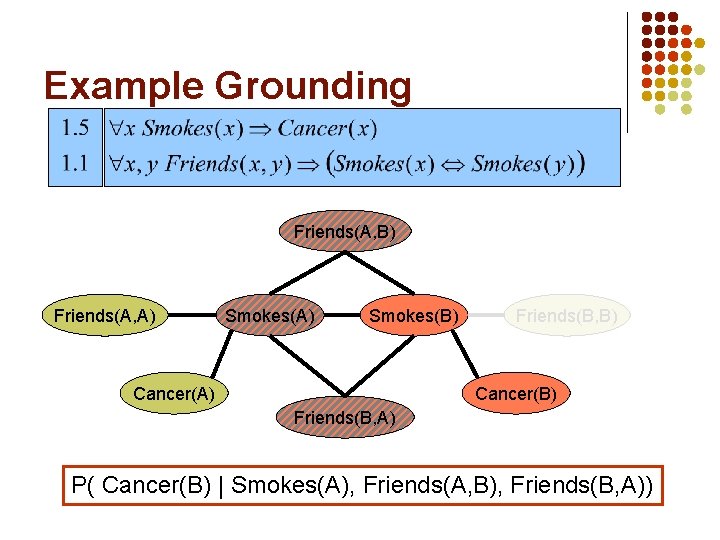
Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

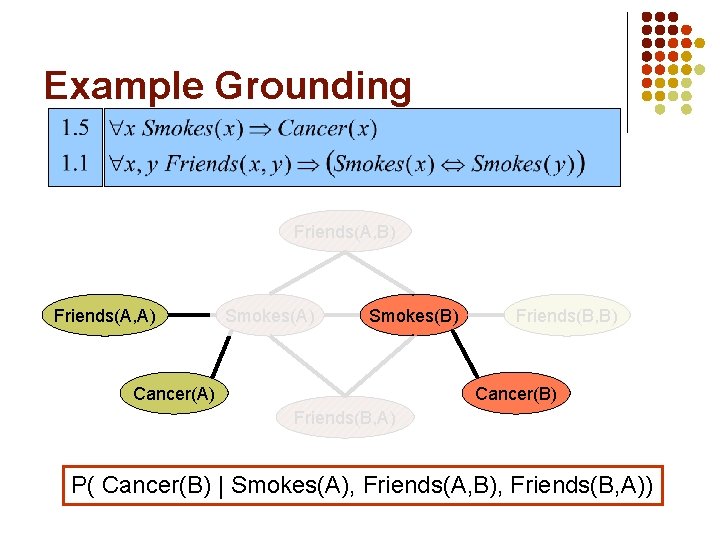
Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

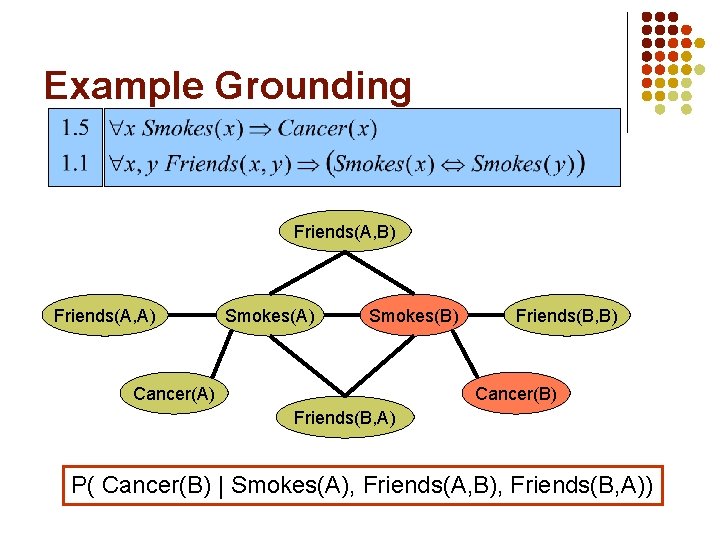
Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

Example Grounding Friends(A, B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A) P( Cancer(B) | Smokes(A), Friends(A, B), Friends(B, A))

Other Options l l Lazy inference Lifted inference

Learning l l Data is a relational database Closed world assumption → Complete data Learning parameters (weights) Learning structure (formulas)

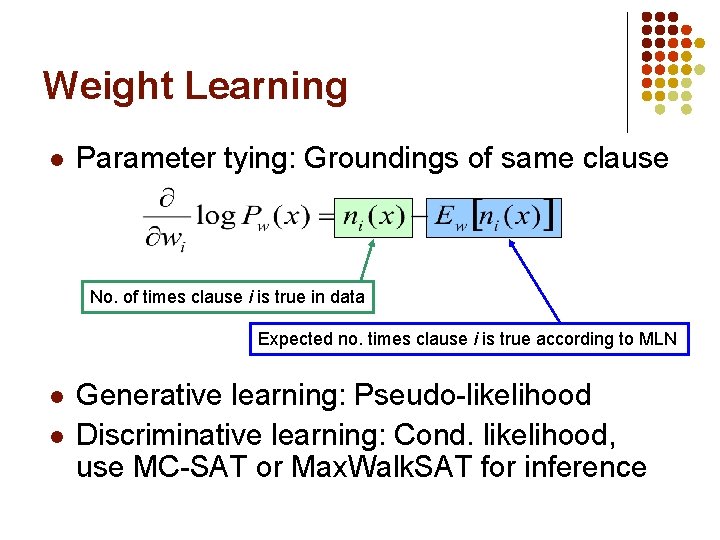
Weight Learning l Parameter tying: Groundings of same clause No. of times clause i is true in data Expected no. times clause i is true according to MLN l l Generative learning: Pseudo-likelihood Discriminative learning: Cond. likelihood, use MC-SAT or Max. Walk. SAT for inference

Structure Learning l l l l Generalizes feature induction in Markov nets Any inductive logic programming approach can be used, but. . . Goal is to induce any clauses, not just Horn Evaluation function should be likelihood Requires learning weights for each candidate Turns out not to be bottleneck Bottleneck is counting clause groundings Solution: Subsampling

Structure Learning l l Initial state: Unit clauses or hand-coded KB Operators: Add/remove literal, flip sign Evaluation function: Pseudo-likelihood + Structure prior Search: Beam, shortest-first, bottom-up, etc.

Alchemy Open-source software including: l Full first-order logic syntax l Inference: MCMC, belief propagation, etc. l Generative & discriminative weight learning l Structure learning l Programming language features alchemy. cs. washington. edu

Example: Information Extraction Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06). Singla, P. , & Domingos, P. (2006). Memory-efficent inference in relatonal domains. In Proceedings of the Twenty-First National Conference on Artificial Intelligence (pp. 500 -505). Boston, MA: AAAI Press. H. Poon & P. Domingos, Sound and Efficient Inference with Probabilistic and Deterministic Dependencies”, in Proc. AAAI-06, Boston, MA, 2006. P. Hoifung (2006). Efficent inference. In Proceedings of the Twenty-First National Conference on Artificial Intelligence.

Segmentation Author Title Venue Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06). Singla, P. , & Domingos, P. (2006). Memory-efficent inference in relatonal domains. In Proceedings of the Twenty-First National Conference on Artificial Intelligence (pp. 500 -505). Boston, MA: AAAI Press. H. Poon & P. Domingos, Sound and Efficient Inference with Probabilistic and Deterministic Dependencies”, in Proc. AAAI-06, Boston, MA, 2006. P. Hoifung (2006). Efficent inference. In Proceedings of the Twenty-First National Conference on Artificial Intelligence.

Entity Resolution Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06). Singla, P. , & Domingos, P. (2006). Memory-efficent inference in relatonal domains. In Proceedings of the Twenty-First National Conference on Artificial Intelligence (pp. 500 -505). Boston, MA: AAAI Press. H. Poon & P. Domingos, Sound and Efficient Inference with Probabilistic and Deterministic Dependencies”, in Proc. AAAI-06, Boston, MA, 2006. P. Hoifung (2006). Efficent inference. In Proceedings of the Twenty-First National Conference on Artificial Intelligence.

Entity Resolution Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06). Singla, P. , & Domingos, P. (2006). Memory-efficent inference in relatonal domains. In Proceedings of the Twenty-First National Conference on Artificial Intelligence (pp. 500 -505). Boston, MA: AAAI Press. H. Poon & P. Domingos, Sound and Efficient Inference with Probabilistic and Deterministic Dependencies”, in Proc. AAAI-06, Boston, MA, 2006. P. Hoifung (2006). Efficent inference. In Proceedings of the Twenty-First National Conference on Artificial Intelligence.

State of the Art l Segmentation l l Entity resolution l l l HMM (or CRF) to assign each token to a field Logistic regression to predict same field/citation Transitive closure Alchemy implementation: Seven formulas

Types and Predicates token = {Parag, Singla, and, Pedro, . . . } field = {Author, Title, Venue} citation = {C 1, C 2, . . . } position = {0, 1, 2, . . . } Token(token, position, citation) In. Field(position, field, citation) Same. Field(field, citation) Same. Cit(citation, citation)

Types and Predicates token = {Parag, Singla, and, Pedro, . . . } field = {Author, Title, Venue, . . . } citation = {C 1, C 2, . . . } position = {0, 1, 2, . . . } Token(token, position, citation) In. Field(position, field, citation) Same. Field(field, citation) Same. Cit(citation, citation) Optional

Types and Predicates token = {Parag, Singla, and, Pedro, . . . } field = {Author, Title, Venue} citation = {C 1, C 2, . . . } position = {0, 1, 2, . . . } Token(token, position, citation) In. Field(position, field, citation) Same. Field(field, citation) Same. Cit(citation, citation) Evidence

Types and Predicates token = {Parag, Singla, and, Pedro, . . . } field = {Author, Title, Venue} citation = {C 1, C 2, . . . } position = {0, 1, 2, . . . } Token(token, position, citation) In. Field(position, field, citation) Same. Field(field, citation) Same. Cit(citation, citation) Query

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Formulas Token(+t, i, c) => In. Field(i, +f, c) ^ !Token(“. ”, i, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

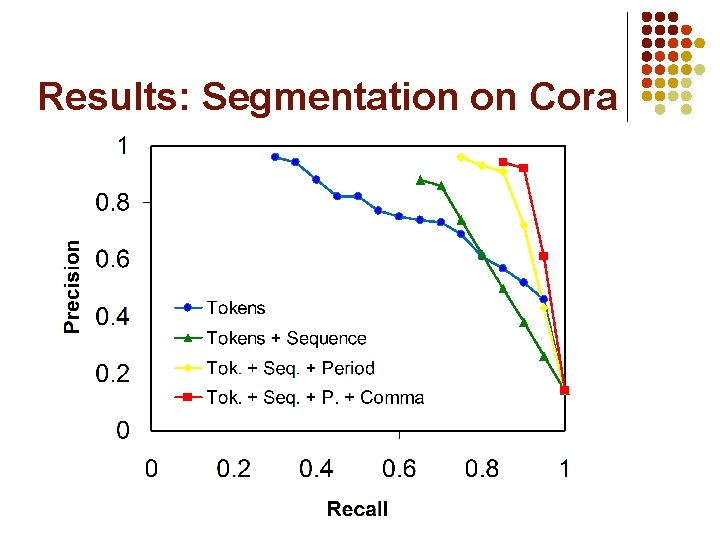
Results: Segmentation on Cora

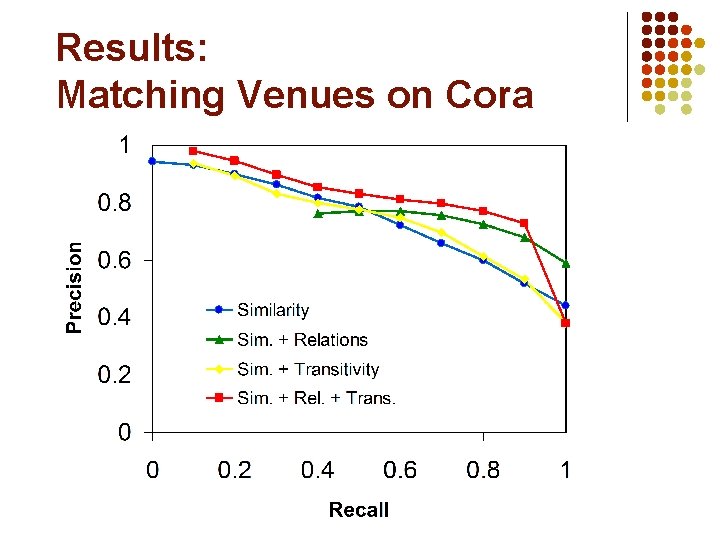
Results: Matching Venues on Cora