Relational Model of Data over Domains with Similarities

Relational Model of Data over Domains with Similarities An Extension for Similarity Queries and Knowledge Extraction Radim Belohlavek Vilem Vychodil Stanislav Opichal Dept. Computer Science Palacky University, Olomouc Czech Republic 1 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Outline problem setting: introducing extended Codd’s model preliminaries from fuzzy logic functional dependencies (as example of data dependencies): Armstrong axioms and completeness, entailment and non-redundant bases, computation of bases relational algebra and calculus practical issues further issues, future research 2 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Problem setting Our paper: contribution to an extension of Codd’s relational model extension concerns uncertainty (imprecision) Abiteboul S. et al. : The Lowell database research self-assessment. Comm. ACM 48(5)(2005), 111– 118: management of uncertainty in the foundations of databases extension: provides framework for approximate matches and related issues (similarity queries, similarity join, . . . ) contrary to exact matches of the classical model we add: similarity relations on domains ranks assigned to tuples in this talk: data dependencies relational algebra and calculus practical issues 3 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Problem setting (cntd. ) Our extension of Codd’s model: (ranked) data tables over domains with similarities ranked table answer to similarity-based query 4 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Problem setting (cntd. ) Related work extensions of Codd’s model employing fuzzy logic several approaches, many papers Raju, Majumdar, Fuzzy functional dependencies and lossless join decomposition of fuzzy relational database systems. ACM Trans. Database Systems Vol. 13, No. 2, 1988, pp. 129– 166. extensions of Codd’s model employing probability different both semantically and technically (probability=fuzzy logic) Fuhr, Rölleke, A probabilistic relational algebra for the integration of information retrieval and database systems. ACM Trans. Information Systems 15: 32– 66, 1997. D. Dey and S. Sarkar S. A probabilistic relational model and algebra. ACM Trans. Dat. Syst. 21: 339– 369, 1996. 5 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Problem setting (cntd. ) related work Fagin at al. R. Fagin. Combining fuzzy information: an overview. ACM SIGMOD Record 31(2): 109 -118, 2002. Natsev, Chang, Smith, Li, Vitter: Supporting incremental join queries on ranked inputs. VLDB 2001, pp. 281– 290. Cohen, Sagiv: An incremental algorithm for computing ranked full disjunctions. PODS 2005, pp. 98– 107. Rank. SQL + related research Li, Chang, Ilyas, Song: Rank. SQL: Query Algebra and Optimization for Relational top-k queries. ACM SIGMOD 2005, pages 131– 142, 2005. Illyas, Aref, Elmagarmid: Supporting top-k join queries in relational databases. The VLDB Journal 13: 207– 221, 2004. 6 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Preliminaries from fuzzy logic invented by Zadeh: simple calculus for handling of vagueness: Zadeh L. A. : Fuzzy sets. Inf. Control (1965). basic principle: allows propositions to have intermediate truth degrees instead of just 0 (false) and 1 (true), e. g. ||John is tall. || = 0. 9, ||A is simiar to B|| = 0. 7 developed since late 1960 s for a long time no firm logical foundations, ad hoc approaches, many results of low quality logical foundations developed in late 1990 s, monographs available 7 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Preliminaries: structures of truth degrees classical logic: two-element Boolean algebra, given by set {0, 1} of truth degrees (truth functions of) logical connectives (conjunction, implication, . . . ) fuzzy logic: several possibilities, a general one: complete residuated lattice, given by (partially ordered) set L of truth degrees, e. g. L = [0, 1], L = {0, 0. 1, 0. 2, . . . , 1}, non-linearly ordered L, . . . (truth functions of) logical connectives (conj. , impl. , . . . ) Complete residuated lattice – basic structure of truth degrees L = L, , , 0, 1 , where L, , , 0, 1 … complete lattice, L, , 1 … commutative monoid, , … adjoint pair (a b c iff a b c). details in proceedings 8 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Our extension of Codd’s model (ranked) data tables over domains with similarities ranked table answer to similarity-based query Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with 9 IDA 2007

Functional dependencies formulas A B (A, B Y , sets of attributes) describing attribute dependencies, e. g. {flight No. } {depart. time, arriv. time} used in knowledge extraction data mining formal concept analysis (attribute implications) interpreted in tables with yes/no-attributes knowledge extraction relational databases (functional dependencies) interpreted in DB relations (tables with general attributes) data redundancy, normalization, DB design, . . . knowledge extraction (Manilla, R¨aiha: Algorithms for inferring functional dependencies from relations, Data & Knowledge Eng. 12: 83– 99. ) 10 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Recalling functional dependencies (FDs). . . ordinary setting table D A B is true in table D means: for any tuples x 1, x 2: IF x 1 and x 2 agree on their values of attributes from A THEN x 1 and x 2 agree on their values of attributes from B Example {y 1, y 2} {y 3} is true in D, {y 1} {y 2} is not (x 2 x 4 counterexample) { flight No. } { departure time, arrival time } 11 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Fuzzy functional dependencies: syntax Definition Fuzzy functional dependence (FFD) over attributes Y : A B, where A, B LY (fuzzy sets of attributes) Example {0. 7/y 1} {0. 3/y 2} {0. 4/y 1, y 2, 0. 1/y 3} {y 3, 0. 5/y 4} {y 1, y 3} {y 4} … ordinary dependence {} … empty Intended meaning of A B • as in ordinary case, but equality replaced by similarity • for any of two tuples x 1, x 2 X IF x 1 and x 2 have similar values on attributes from A THEN x 1 and x 2 have similar values on attributes from B • new kind of dependencies (data mining apeal) • A B can be true to a degree from L, not only 0 or 1 • degrees A(y), B(y) act as tresholds Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with 12 IDA 2007

Semantics of FFDs D … table with similarities (for simplicity, ranks=1) Definition (degree ||A B||D to which A B is true in … defined by ||A B||D D x x X((x (A) x (A))* ((x (B) x (B)) 1 2 1 2 Remark Ordinary meaning of functional dependencies is a particular case: A and B ordinary sets, y ordinary equality for each y Y. 13 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Semantics of FFD: models, entailment D … table with similarities Definition (models and entailment in ranked tables) T … a set of T of FFDs models of T: Mod(T ) = { … in words: D I for each A B T : ||A B||D = 1}, D is a model of T means “each FFD from T is true in D” Definition (models and entailment in ranked tables) T … a set (fuzzy set) of T of FFDs degree of entailment of A B from T: ||A B||T = D Mod(T ) ||A B||D … in words: a degree to which A B follows from T = degree of “A B is true in each model of T ” Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with 14 IDA 2007

Armstrong-like rules, provability, and completeness Recall: Armstrong W. W. : Dependency structures in data base relationships. IFIP Congress, Geneva, Switzerland, 1974. a system of deduction rules s. t. A B is entailed by T iff A B is provable from T in our setting, entailment is a matter of degree, two concepts of provability and completeness: ordinary completeness (interesting only degree 1): φ follows from T iff φ provable from T graded completeness (any degree interesting): degree to which φ follows from T = = degree of provability of φ from T. We present a syntactico-semantically complete (both types) system of Armstrong-like rules. 15 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Armstrong-like rules, provability, and completeness Deduction rules: rules describing what FFDs can be inferred (in one elementary step) from other FFDs inspired by Armstrong-like rules, several equivalent systems one of them (an elegant one) is “classical” Armstrong rules + “fuzzy rule” 16 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Ordinary provability and completeness Provability: T. . . theory (set of FFDs) A B is provable from T, written T ⊢ A B, if there is a sequence φ1, . . . , φn of FFDs such that i. φn is A B, ii. for each φ i : φ i 2 T or 'i is inferred from the preceding formulas (i. e. , φ1, . . . , φi− 1) using one of the deduction rules (Ax)–(Cut). Provability: bivalent notion (either T ⊢ A B or T ⊬ A B). Theorem (ordinary completeness) ||A B||T = 1 ( A B follows from T, in degree 1) iff T ⊢ A B (A B is provable from T) 17 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Graded provability and completeness Provability: bivalent notion (either T ⊢ A B or T ⊬ A B). can we capture a degree of semantic entailment syntactically? (i. e. , by a modification of the concept of proof) Graded provability. . . set of FFDs |A B |T ∈ L … degree which A B is provable from T (details proceedings) Theorem (graded completeness) ||A B ||T = |A B |T (degree of entailment = degree of provability). 18 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Non-redundant bases of FFDs aim: large sets of FFDs small sets of FFDs (equally informative) example: Given ranked table D with similarities, extract true FFDs from D, but only the essential ones Definition (complete set of FFDs) A set T of FFDs is complete in D if 1. for each A B ∈ T : ||A B||D = 1 (each FFD from T is true in D) 2. for each A B : ||A B||D = ||A B||T complete set T of D fully describe validity of FFDs in D 19 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Non-redundant bases of FFDs (cntd. ) Definition (Non-redundant bases of D) A set T of FFDs a non-redundant basis of 1. 2. D if T is complete in D No T′ ⊂ T is complete In what follows: computation of particular non-redundant bases based on so-called pseudo-intents 20 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Non-redundant bases using pseudo-intents Definition (pseudo-intents of D) A system of pseudo-intents of a ranked table D with similarities is a system P of fuzzy sets of attributes such that P∈ P iff (detailed description in proceedings) the role of pseudo-intents: Theorem (non-redundant basis based on pseudo-intents) If P is a system of pseudo-intents then T = { P C (P ) | P ∈ is a non-redundant basis of P} D C(P) is a particular modification of P, details omitted. Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with 21 IDA 2007

Computing pseudo-intents (+non-redundant bases) Theorem (pseudo-intents from fixpoints of cl. T* ) Let P be a system of pseudo-intents of D. Then P = { P ∈ fix(cl. T* ) | P ≠ C (P ) } Where of cl. T* is defined by: For Z ∈ LY we put . . . operator on L-sets in Y fix(cl. T* ) = {P | cl. T* (P) = P}. . . fixpoints of cl. T* Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with 22 IDA 2007

Computing non-redundant bases (algorithm) Input: D (data table over dom. with similarity relations). Output: P (system of pseudo intents) B≔ 0 if B ≠ C(B ): add B to P while B ≠ Y : T ≔ { P C (P ) | P ∈ P } B ≔ B+ (B+ is lectically smallest fixed point of cl. T* which is a successor of B) if B ≠ C(B ): add B to P polynomial time delay complexity 23 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Relational algebra and calculus basic traits (details in proceedings and a forthcoming paper): extension of classical relational algebra which takes similarities into account relational algebra — operations: counterparts to Boolean operations (union, . . . ) new operations arising within the framework of fuzzy logic (e. g. based on thresholds, like a-cut: [a. D](t) = {t |D (t) ≥ a}) operations where exact matches are extended by similarity-based matches (selection, join, . . . ) further operations: e. g. topk (best k tuples satisfying a query considerable interest) relational calculus: based on formal predicate fuzzy logic (essential are nonstandard issues like quantifiers “most”, etc. ) well-founded like in the classical case: Theorem (equivalence theorem) Relational algebra and relational calculus for the extended model are equivalent. 24 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

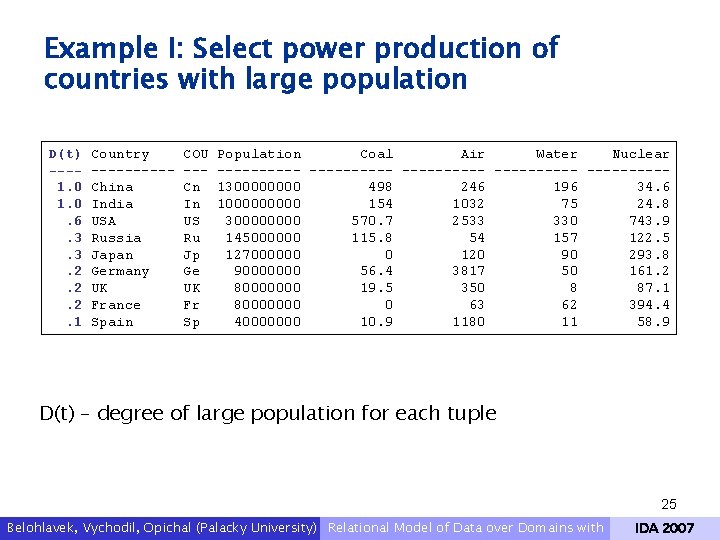
Example I: Select power production of countries with large population D(t) ---1. 0. 6. 3. 3. 2. 2. 2. 1 Country -----China India USA Russia Japan Germany UK France Spain COU --Cn In US Ru Jp Ge UK Fr Sp Population Coal Air Water Nuclear ---------- -----130000 498 246 196 34. 6 100000 154 1032 75 24. 8 30000 570. 7 2533 330 743. 9 145000000 115. 8 54 157 122. 5 127000000 0 120 90 293. 8 90000000 56. 4 3817 50 161. 2 80000000 19. 5 350 8 87. 1 80000000 0 63 62 394. 4 40000000 10. 9 1180 11 58. 9 D(t) – degree of large population for each tuple 25 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Implementation of domains with similarities I Similarity of power production from coal is defined by table ≈c Cn In US Ru Jp Ge Fr UK Sp ─────────────── Cn 1. 3 In 1. 6 US. 3 1 Ru. 6 1. 4 Jp 1. 4 1. 8. 9 Ge. 4. 4 1. 4. 7. 6 Fr 1. 4 1. 8. 9 UK. 8. 7. 8 1 1 Sp. 9. 6. 9 1 1 Similarity table DDL CREATE TABLE t_sim_coal ( country_code 1 VARCHAR(2), country_code 2 VARCHAR(2), similarity NUMBER(3, 2), CONSTRAINT t_sim_coal_pk PRIMARY KEY ( country_code 1, country_code 1 ) ); COUNTRY_CODE 1 ------Cn Cn In In US Ru. . . COUNTRY_CODE 2 SIMILARITY -------Cn 1 US. 3 In 1 Ru. 6 US 1 Ru 1 26 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Similarity defined by table – performance issues Similarity for two countries is retrieved by join in following steps – let’s suppose that both country codes are available from a main loop 1. Find out a ROWID in the index t_sim_coal_pk for the two given country codes 2. Retrieve similarity from the table t_sim_coal using the ROWID and provide it for further query execution It is obvious that there is additional step – retrieving of the ROWID. But the ROWID is not necessary for result. t_sim_coal should be replaced by database structure supporting searching, which gives the similarity value immediately instead of the ROWID (i. e. index organized table) Similarity table DDL CREATE TABLE t_sim_coal ( country_code 1 VARCHAR(2), country_code 2 VARCHAR(2), similarity NUMBER(3, 2), CONSTRAINT t_sim_coal_pk PRIMARY KEY ( country_code 1, country_code 1 ) ); COUNTRY_CODE 1 ------Cn Cn In In US Ru. . . COUNTRY_CODE 2 SIMILARITY -------Cn 1 US. 3 In 1 Ru. 6 US 1 Ru 1 27 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Implementation of domains with similarities II Ranking of large population is defined by function Definition in RDBMS with procedural extension function large_population ( p_population in varchar 2 ) return number is large_popul_c constant number : = 50000; l_ret number : =0; begin return least( p_population/large_popul_c, 1 ); end; / 28 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

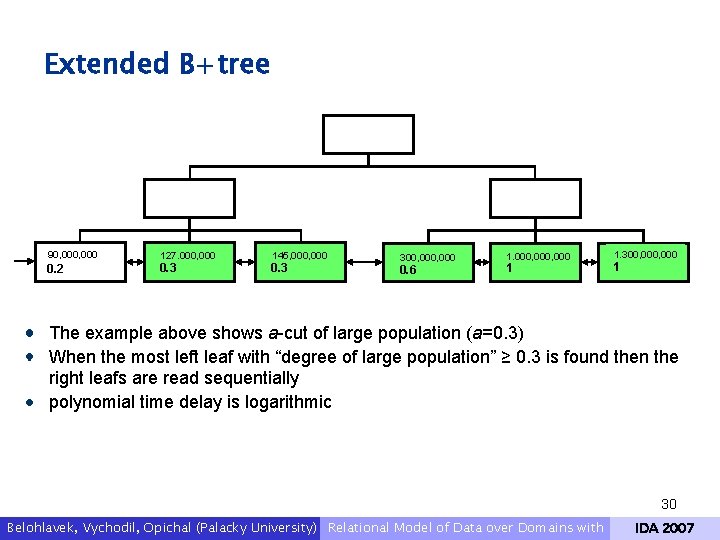
Ranking defined by function - performance considerations Ranking or similarity defined by function can lead to decreased performance during SQL execution on large data It is possible to created an index based on function using row columns as parameters. But the index transforms the result to ROWID which is not very helpful Extending classical B+tree by a degree values in the leaves. The leaves would consist of indexed column, the degree value and the ROWID. The extended B+tree would support operations like topk or a-cut very effectively provided that ranking function is monotonous 29 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Extended B+tree 90, 000 0. 2 127, 000 0. 3 145, 000 0. 3 300, 000 0. 6 1, 000, 000 1 1, 300, 000 1 The example above shows a-cut of large population (a=0. 3) When the most left leaf with “degree of large population” ≥ 0. 3 is found then the right leafs are read sequentially polynomial time delay is logarithmic 30 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Implementation of ranked table in ORDBMS (cntd. ) Let’s define object view Definition of object type in ORDBMS Oracle 10 g create or replace type powerprod_t AS OBJECT ( country varchar 2(30), population number, coal number, air number, water number, nuclear number, MEMBER FUNCTION similar_coal(itupple in powerprod_t) return number, MEMBER FUNCTION similar_air(itupple in powerprod_t) return number, MEMBER FUNCTION similar_water(itupple in powerprod_t) return number, MEMBER FUNCTION similar_nuclear(itupple in powerprod_t) return number, MEMBER FUNCTION large_popul(itupple in powerprod_t) return number ); 31 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Implementation of ranked table in ORDBMS (cntd. ) Let’s define object view over the table t_countries using object type powerprod_t. Definition of object view powerprod_v in ORDBMS Oracle 10 g create or replace view powerprod_v of powerprod_t with object identifier (country) as select country, population, coal, air, water, nuclear from t_countries; 32 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

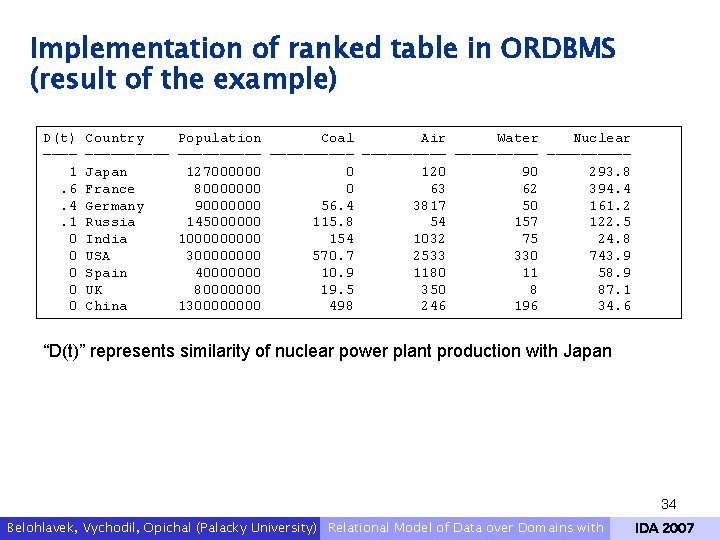
Implementation of ranked table in ORDBMS (cntd. ) And now we can select i. e. all countries having similar power production from nuclear power plats Definition of object view powerprod_v in ORDBMS Oracle 10 g select a. similar_nuclear(value(b)) "D(t)", a. country "Country", a. population "Population", a. coal "Coal", a. air "Air", a. water "Water", a. nuclear "Nuclear" from powerprod_v a, powerprod_v b where b. country='Japan' order by 1 desc / “D(t)” represents similarity of nuclear power plant production with Japan Note, that similar_nuclear search similarities in the table t_sim_nuclear 33 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Implementation of ranked table in ORDBMS (result of the example) D(t) ———— 1. 6. 4. 1 0 0 0 Country ————— Japan France Germany Russia India USA Spain UK China Population Coal Air Water Nuclear —————————— ————— 127000000 0 120 90 293. 8 80000000 0 63 62 394. 4 90000000 56. 4 3817 50 161. 2 145000000 115. 8 54 157 122. 5 100000 154 1032 75 24. 8 30000 570. 7 2533 330 743. 9 40000000 10. 9 1180 11 58. 9 80000000 19. 5 350 8 87. 1 130000 498 246 196 34. 6 “D(t)” represents similarity of nuclear power plant production with Japan 34 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007

Future research further study of extended Codd’s model (foundations, algorithms, implementation), connection to existing work on Rank. SQL, to work on algorithms, . . . , further data dependencies, data redundancy (approximate redundancy), data mining aspects, implications true in degrees other than 1 (at least a, etc. ): bases, . . . involve tolerance: e. g. “almost complete” basis, can it be smaller? . . . 35 Belohlavek, Vychodil, Opichal (Palacky University) Relational Model of Data over Domains with IDA 2007