RELATIONAL ALGEBRA II Unary Relational Operations SELECT and

RELATIONAL ALGEBRA (II)

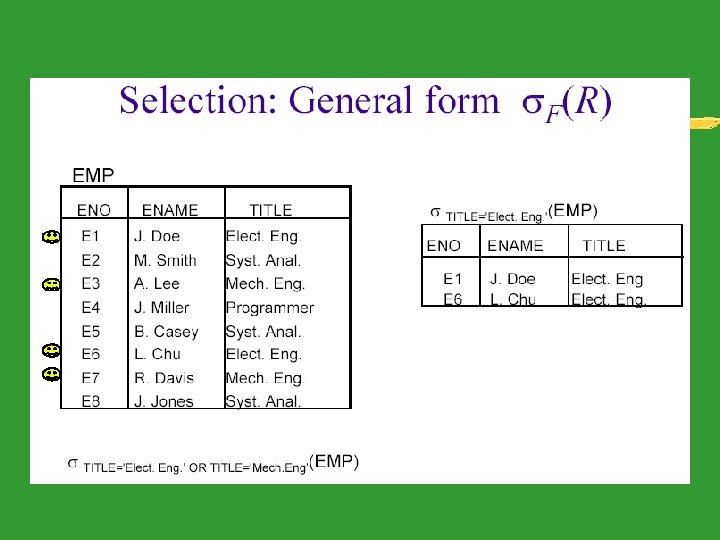
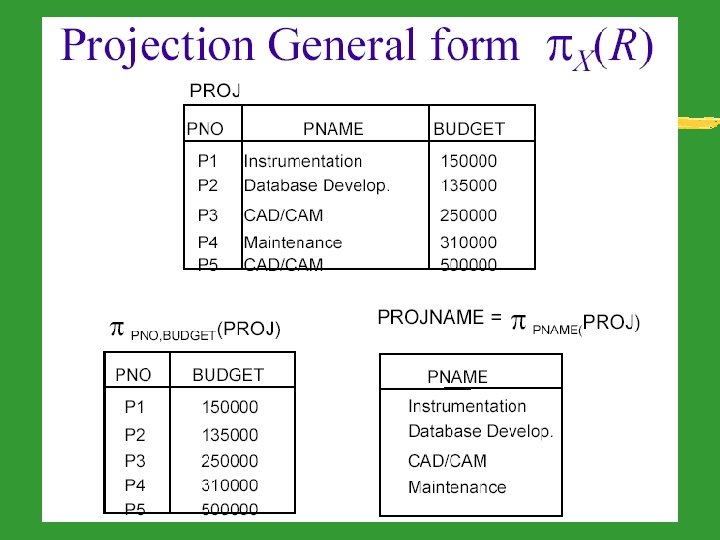
Unary Relational Operations: SELECT and PROJECT z. The PROJECT Operation z. Sequences of Operations and the RENAME Operation z. The SELECT Operation

Relational Algebra Operations from Set Theory z. The UNION, INTERSECTION, and MINUS Operations

Binary Relational Operations: JOIN and DIVISION z. The JOIN Operation z. The EQUIJOIN and NATURAL JOIN Variations of JOIN z. A Complete Set of Relational Algebra Operations z. The DIVISION Operation

Additional Relational Operations z. Aggregate Functions and Grouping z. Recursive Closure Operations z. OUTER JOIN Operations z. The OUTER JOIN Operation

SPECIAL RELATIONAL OPERATORS The following operators are peculiar to relations: - Join operators There are several kind of join operators. We only consider three of these here (others will be considered when we discuss null values): - (1) Condition Joins - (2) Equijoins - (3) Natural Joins - Division

JOIN OPERATORS Condition Joins: - Defined as a cross-product followed by a selection: R ⋈c S = σc(R S) (⋈ is called the bow-tie) where c is the condition. - Example: Given the sample relational instances S 1 and R 1 The condition join S ⋈S 1. sid<R 1. sid R 1 yields

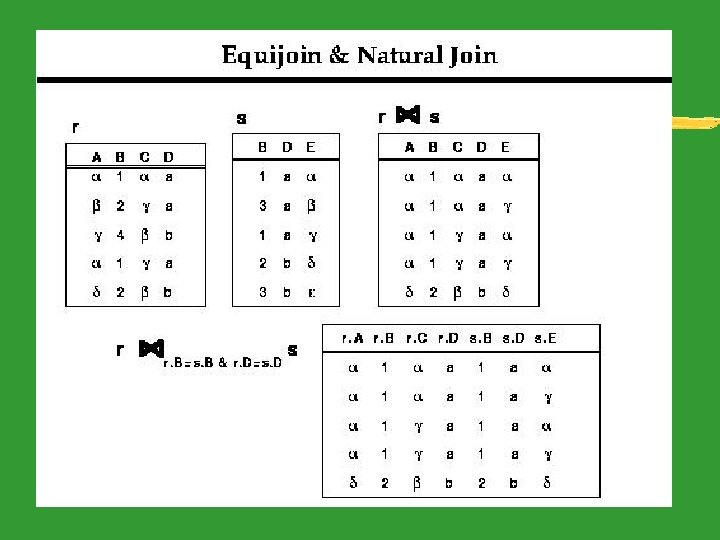
Equijoin: Special case of the condition join where the join condition consists solely of equalities between two fields in R and S connected by the logical AND operator (∧). Example: Given the two sample relational instances S 1 and R 1 The operator S 1 R. sid=Ssid R 1 yields

Natural Join - Special case of equijoin where equalities are implicitly specified on all fields having the same name in R and S. - The condition c is now left out, so that the “bow tie” operator by itself signifies a natural join. - N. B. If the two relations have no attributes in common, the natural join is simply the cross-product.

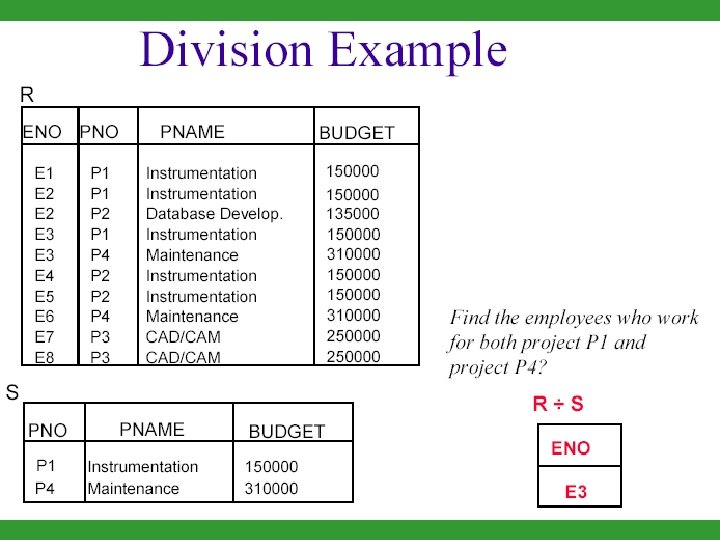
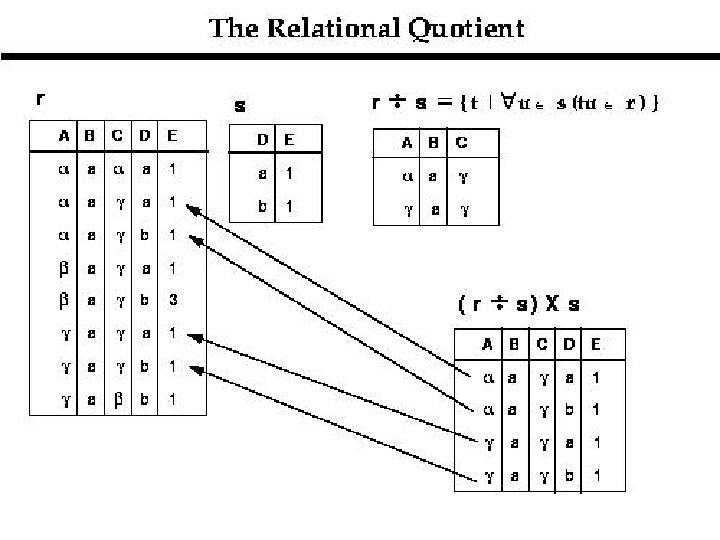
DIVISION - The division operator is used for queries which involve the ‘all’ qualifier such as “Find the names of sailors who have reserved all boats”. - The division operator is a bit tricky to explain.

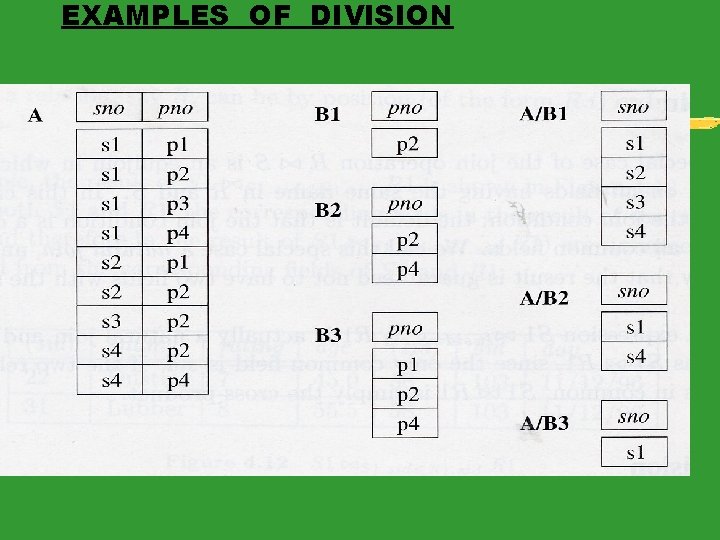
EXAMPLES OF DIVISION

DIVISION Example: Find the names of sailors who have reserved all boats: (1) A = sid, bid(Reserves). A 1 = sid(Reserves) A 2 = bid(Reserves) (2) B 2 = bid(Boats) B 3 is the rest of B. Thus, B 2 ={101, 102, 103, 104} (3) Find the rows of A such that their A. sid is the same and their combined A. bid is the set B 2. Thus we find A 1 = {22} (4) Get the set of A 2 corresponding to A 1: A 2 = {Dustin}

FORMAL DEFINITION OF DIVISION The formal definition of division is as follows: A/B = x(A) - x(( x(A) B) – A)

EXAMPLES OF ALGEBRA QUERIES In the rest of this chapter we shall illustrate queries using the following new instances S 3 of sailors, R 2 of Reserves and B 1 of boats.

QUERY Q 1 Given the relational instances: (Q 1) Find the names of sailors who have reserved boat 103 sname((σbid=103 Reserves) ⋈ Sailors) The answer is thus the following relational instance {<Dustin>, <Lubber>, <Horatio>}

QUERY Q 1 (cont’d) There are of course several ways to express Q 1 in relational algebra. Here is another: sname(σbid=103(Reserves⋈ Sailors)) Which of these expressions should we use? That is a question of optimization. Indeed, when we describe how to state queries in SQL, we can leave it to the optimizer in the DBMS to select the nest approach.

QUERY Q 2 (Q 2) Find the names of sailors who have reserved a red boat. sname((σcolor=‘red’Boats) ⋈ Reserves ⋈ Sailors)

QUERY Q 3 (Q 3) Find the colors of boats reserved by Lubber. color((σsname=‘Lubber’Sailors)Sailors ⋈ Reserves ⋈ Boats)

QUERY Q 4 (Q 4) Find the names of Sailors who have reserved at least one boat sname(Sailors ⋈ Reserves)

QUERY Q 5 (Q 5) Find the names of sailors who have reserved a red or a green boat. (Tempboats, (σcolor=‘red’Boats) ∪ (σcolor=‘green’Boats)) sname(Tempboats ⋈ Reserves ⋈ Sailors)

QUERY Q 6 (Q 6) Find the names of Sailors who have reserved a red and a green boat. It seems tempting to use the expression used in Q 5, replacing simply ∪ by ∩. However, this won’t work, for such an expression is requesting the names of sailors who have requested a boat that is both red and green! The correct expression is as follows: (Tempred, sid((σcolor=‘red’Boats) ⋈ Reserves)) (Tempgreen, sid((σcolor=‘green’Boats) ⋈ Reserves)) sname ((Tempred ∩ Tempgreen) ⋈ Sailors)

QUERY Q 7 (Q 7) Find the names of sailors who have reserved at least two boats. (Reservations, sid, sname, bid(Sailors ⋈ Reserves)) (Reservationpairs(1 sid 1, 2 sname, 3 bid 1, 4 sid 2, 5 sname, 6 bid 2), Reservations) sname 1σ(sid 1=sid 2) (bid 1 bid 2)Reservationpairs)

QUERY 8 (Q 8) Find the sids of sailors with age over 20 who have not reserved a red boat. sid(σage>20 Sailors) - sid((σcolor=‘red’Boats) ⋈ Reserves ⋈ Sailors)

QUERY 9 (Q) Find the names of sailors who have reserved all boats. (Tempsids, ( sid, bid. Reserves) / ( bid. Boats)) sname(Tempsids ⋈ Sailors

QUERY Q 10 (Q 10) Find the names of sailors who have reserved all boats called Interlake. (Tempsids, ( sid, bid. Reserves)/( bid(σbname=‘Interlake’Boats))) sname(Tempsids ⋈ Sailors)

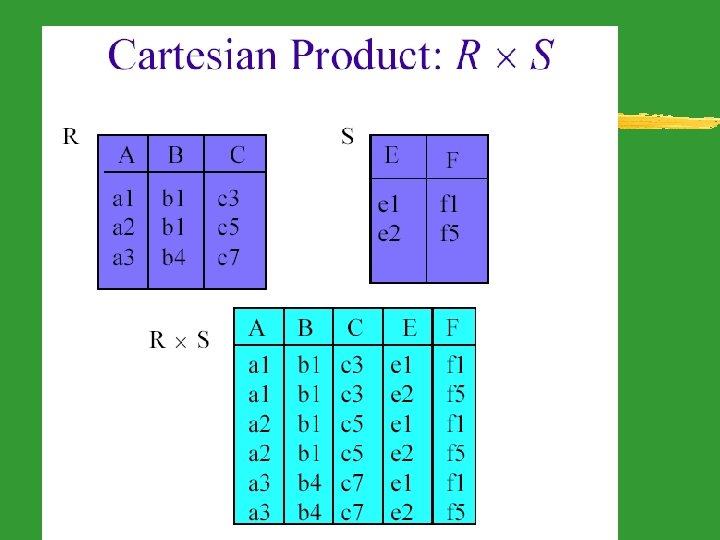
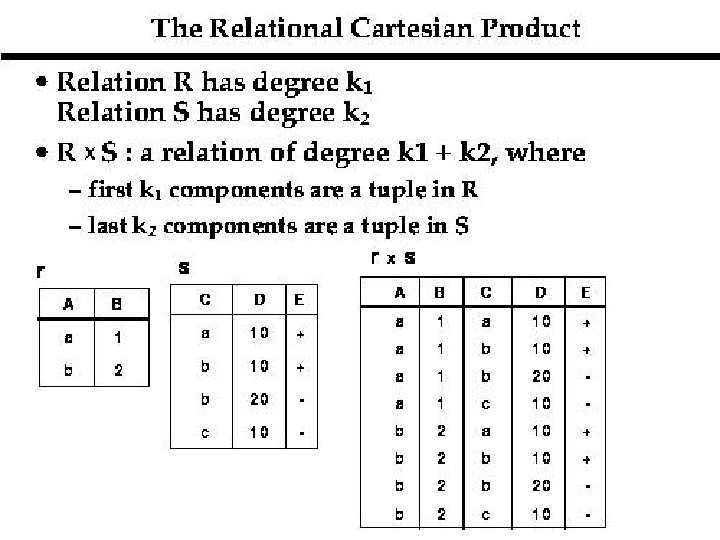
Cartesian Product z. R(A 1, A 2, . . . , Am) and S(B 1, B 2, . . . , Bn) z. T(A 1, A 2, . . . , Am, B 1, B 2, . . . , Bn) = R(A 1, A 2, . . . , Am) X S(B 1, B 2, . . . , Bn) z. A tuple t is in T if and only if t[A 1, A 2, . . . , Am] is in R and t[B 1, B 2, . . . , Bn] is in S. - If R has N 1 tuples and S has N 2 tuples, then T will have N 1*N 2 tuples.

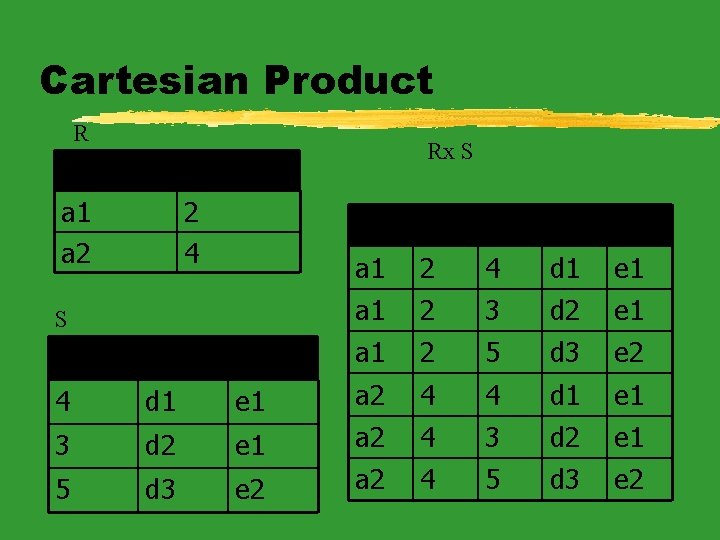
Cartesian Product R A a 1 a 2 Rx S B 2 4 S A B C D E a 1 2 4 d 1 e 1 a 1 2 3 d 2 e 1 C D E a 1 2 5 d 3 e 2 4 d 1 e 1 a 2 4 4 d 1 e 1 3 d 2 e 1 a 2 4 3 d 2 e 1 5 d 3 e 2 a 2 4 5 d 3 e 2

Examples of Queries in Relational Algebra

Natural-Join z. Denoted by |x|. z. Binary operation z. Creates a Cartesian-product of the arguments then performs selection to force equality on attributes that appear in both relations

Division z. Denoted by z. Binary Operation z. Used in queries that include the phrase “for all”.

Division (Cont’d) z. Division is an operation on schema R – S z. A tuple t is in r s if and only if: zt is in ΠR – S(r) and z. For every tuple ts in s, there is a tuple tr in r satisfying both of the following: a. tr[S] = ts[R] b. tr[R – S] = t

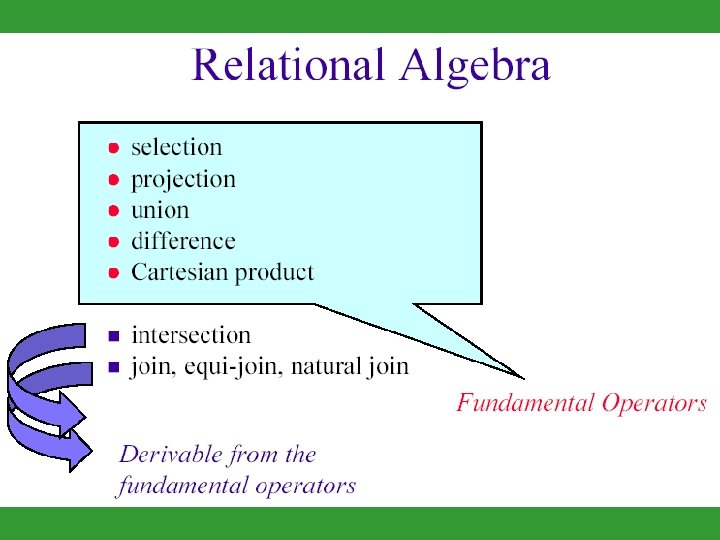
Relational Algebra Fundamental operators z select z project z cartesian product z union z set difference s p - Other operators z natural join z set intersection z division JOIN (butterfly symbol)

A Simple DB account had transaction account ac# owner ss# balance 1 bob 123 1000 2 sue 456 2000 3 jane 789 3000 transaction t# ac# type amount outcome 1 1 W 1500 bounced 2 2 D 1000 ok 3 1 W 100 ok 4 3 D 500 ok 5 2 W 200 ok date 5/1/98 5/2/98 5/4/98 5/7/98 5/9/98

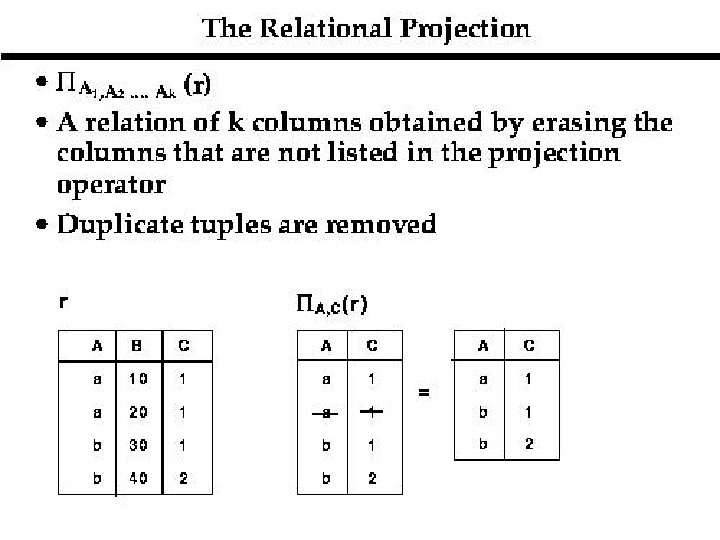
Select s balance>=1500 account eg: result : ac# owner ss# balance 2 sue 456 2000 3 jane 789 3000 Project eg: π result: owner, ss# account owner bob sue jane ss# 123 456 789

Cartesian product eg: account transaction y this will have 15 rows like the ones shown below: ac# owner ss# balance t# type amount outcome date 1 bob 123 1000 1 W 1500 bounced 5/1/98 2 sue 456 2000 2 D 1000 ok 5/2/98 …………… Composing operations eg: “show all transactions done by account owner Bob”. σ account. ano= transaction. ano((s owner=“Bob” account) transaction)

z. Natural Join - combines σ, π, - very commonly used Natural Join forms the cross product of its two arguments, does a selection to enforce equality of columns with the same name and removes duplicate columns. Eg: “show all transactions done by account owner Bob” σ owner=“Bob” (account JOIN transaction)

Rename operation What if you need to access the same relation twice in a query? eg. person(ss#, name, mother_ss#, father_ss#) “Find the name of Bob’s mother” needs the “person” table to be accessed twice. The operation ρ x (r) evaluates to a second logical copy of relation r renamed to x.

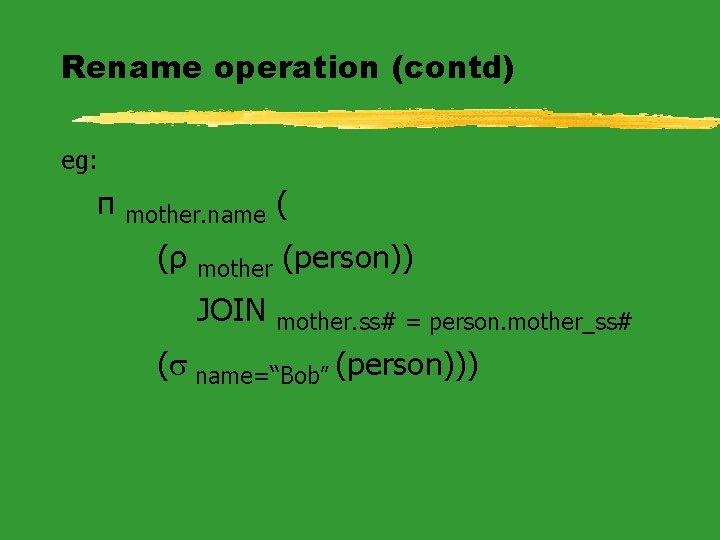
Rename operation (contd) eg: π mother. name (ρ ( mother (person)) JOIN mother. ss# = person. mother_ss# (s name=“Bob” (person)))