Relational Algebra Database Systems 1 What is an

Relational Algebra Database Systems 1

What is an “Algebra” u. Mathematical system consisting of: w Operands --- variables or values from which new values can be constructed. w Operators --- symbols denoting procedures that construct new values from given values. 2

What is Relational Algebra? u. An algebra whose operands are relations or variables that represent relations. u. Operators are designed to do the most common things that we need to do with relations in a database. w The result is an algebra that can be used as a query language for relations. 3

Core Relational Algebra u. Union, intersection, and difference. w Usual set operations, but require both operands have the same relation schema. u. Selection: picking certain rows. u. Projection: picking certain columns. u. Products and joins: compositions of relations. u. Renaming of relations and attributes. 4

Relational Algebra u. Procedural language u. Six basic operators w select: w project: w union: w set difference: – w Cartesian product: x w rename: u. The operators take one or two relations as inputs and produce a new relation as a result.

The SELECT Operation u. SELECT extracts tuples from a relation w result has same relation schema as operand u. SELECT requires a selection condition w selection condition is a boolean expression to filter tuple values u. Syntax: <selection condition> (R) u. Selection condition may contain AND, OR, NOT, =, <, , >, ,

Selection u. R 1 : = SELECTC (R 2) w C is a condition (as in “if” statements) that refers to attributes of R 2. w R 1 is all those tuples of R 2 that satisfy C. 7

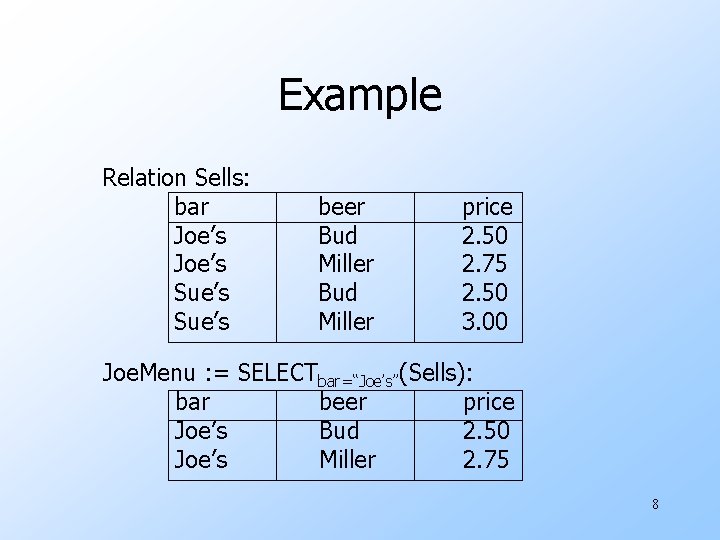
Example Relation Sells: bar Joe’s Sue’s beer Bud Miller price 2. 50 2. 75 2. 50 3. 00 Joe. Menu : = SELECTbar=“Joe’s”(Sells): bar beer price Joe’s Bud 2. 50 Joe’s Miller 2. 75 8

SELECT Examples r 2(STORESTOCK) = < "S 002", "I 065", 120 >, < "S 333", "I 954", 198 >, < "S 047", "I 099", 267 >, < "S 047", "I 954", 300 > Store. Id = "S 047" (STORESTOCK) < "S 047", "I 099", 267 >, < "S 047", "I 954", 300 > quantity < 200 (STORESTOCK) < "S 002", "I 065", 120 >, < "S 333", "I 954", 198 >

The PROJECT Operation u. PROJECT extracts attributes from a relation w result schema attributes are a subset of the operand schema u. PROJECT requires a attribute list u. Syntax: <attribute list> (R) u. Duplicates are not kept in result w result is a relation, which is a set

Projection u. R 1 : = PROJL (R 2) w L is a list of attributes from the schema of R 2. w R 1 is constructed by looking at each tuple of R 2, extracting the attributes on list L, in the order specified, and creating from those components a tuple for R 1. w Eliminate duplicate tuples, if any. 11

Example Relation Sells: bar Joe’s Sue’s beer Bud Miller Prices : = PROJbeer, price(Sells): beer price Bud 2. 50 Miller 2. 75 Miller 3. 00 price 2. 50 2. 75 2. 50 3. 00 12

Composing Operations r(STOCKITEM) = < "I 075", "Ice Cream", $1. 49, false >, < "I 345", "Cupcakes", $1. 99, false >, < "I 333", "Twinkies", $1. 98, false > Price ( Description="Ice Cream" (STOREITEM)) SELECT result: PROJECT result: < "I 075", "Ice Cream", $1. 49, false > < $1. 49 >

Product u. R 3 : = R 1 * R 2 w Pair each tuple t 1 of R 1 with each tuple t 2 of R 2. w Concatenation t 1 t 2 is a tuple of R 3. w Schema of R 3 is the attributes of R 1 and R 2, in order. w But beware attribute A of the same name in R 1 and R 2: use R 1. A and R 2. A. 14

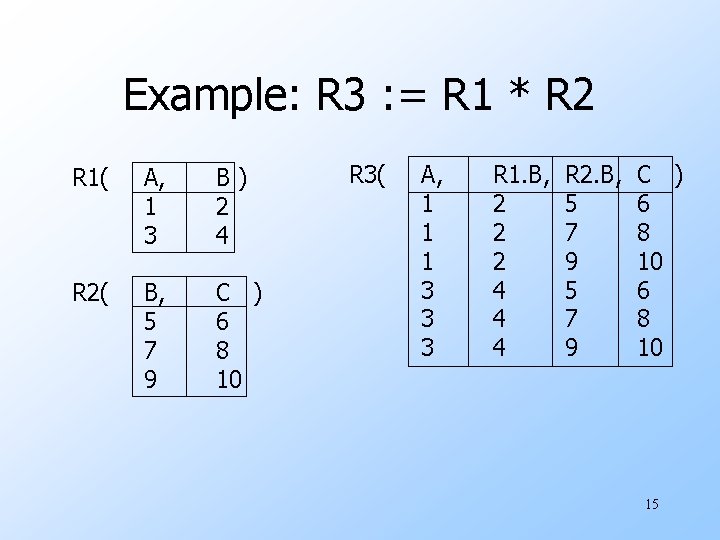
Example: R 3 : = R 1 * R 2 R 1( A, 1 3 B) 2 4 R 2( B, 5 7 9 C ) 6 8 10 R 3( A, 1 1 1 3 3 3 R 1. B, 2 2 2 4 4 4 R 2. B, 5 7 9 C ) 6 8 10 15

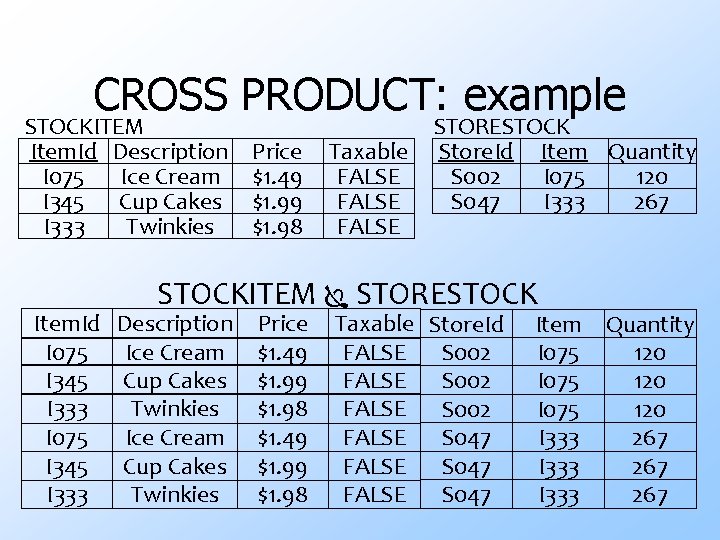
CROSS PRODUCT: example STOCKITEM Item. Id Description Price I 075 Ice Cream $1. 49 I 345 Cup Cakes $1. 99 I 333 Twinkies $1. 98 Taxable FALSE STORESTOCK Store. Id Item Quantity S 002 I 075 120 S 047 I 333 267 STOCKITEM STORESTOCK Item. Id Description I 075 Ice Cream I 345 Cup Cakes I 333 Twinkies Price $1. 49 $1. 99 $1. 98 Taxable Store. Id FALSE S 002 FALSE S 047 Item I 075 I 333 Quantity 120 120 267 267

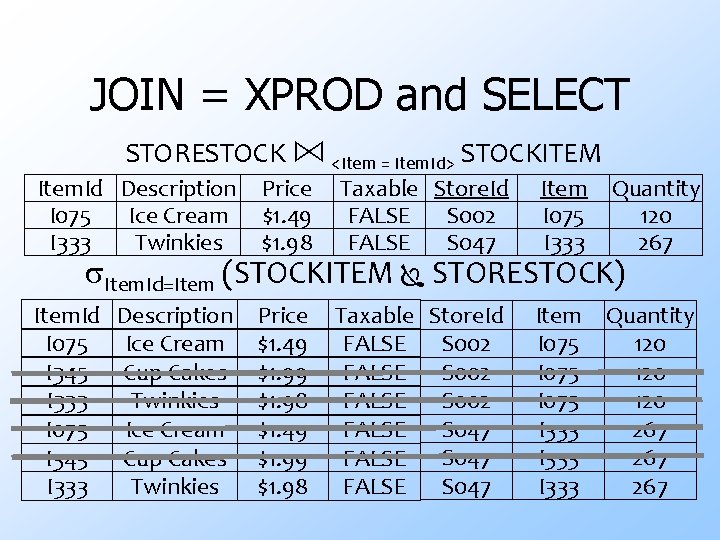
JOIN = XPROD and SELECT STORESTOCK ⋈ <Item = Item. Id> STOCKITEM Item. Id Description I 075 Ice Cream I 333 Twinkies Price $1. 49 $1. 98 Taxable Store. Id Item Quantity FALSE S 002 I 075 120 FALSE S 047 I 333 267 Item. Id=Item (STOCKITEM STORESTOCK) Item. Id Description I 075 Ice Cream I 345 Cup Cakes I 333 Twinkies Price $1. 49 $1. 99 $1. 98 Taxable Store. Id FALSE S 002 FALSE S 047 Item I 075 I 333 Quantity 120 120 267 267

The JOIN Operation u. JOIN combines tuples from two tables based on values of related attributes (usually a FK) u. JOIN requires a join condition w boolean expression comparing attributes from each operand u. Syntax: R⋈ <join condition> S u. The join condition may contain AND, =, <, , >, ,

Theta-Join u. R 3 : = R 1 JOINC R 2 w Take the product R 1 * R 2. w Then apply SELECTC to the result. u. As for SELECT, C can be any booleanvalued condition. w Historic versions of this operator allowed only A theta B, where theta was =, <, etc. ; hence the name “theta-join. ” 19

Example Sells( bar, Joe’s Sue’s beer, Bud Miller Bud Coors price ) 2. 50 2. 75 2. 50 3. 00 Bar. Info : = Sells JOIN Bar. Info( bar, Joe’s Sue’s Bars( name, addr ) Joe’s Maple St. Sue’s River Rd. Sells. bar = Bars. name beer, Bud Miller Bud Coors price, 2. 50 2. 75 2. 50 3. 00 Bars name, addr ) Joe’s Maple St. Sue’s River Rd. 20

Natural Join u. A frequent type of join connects two relations by: w Equating attributes of the same name, and w Projecting out one copy of each pair of equated attributes. u. Called natural join. u. Denoted R 3 : = R 1 JOIN R 2. 21

Example Sells( bar, Joe’s Sue’s beer, Bud Miller Bud Coors price ) 2. 50 2. 75 2. 50 3. 00 Bars( bar, addr ) Joe’s Maple St. Sue’s River Rd. Bar. Info : = Sells JOIN Bars Note Bars. name has become Bars. bar to make the natural join “work. ” Bar. Info( bar, Joe’s Sue’s beer, Bud Milller Bud Coors price, 2. 50 2. 75 2. 50 3. 00 addr ) Maple St. River Rd. 22

Renaming u. The RENAME operator gives a new schema to a relation. u. R 1 : = RENAMER 1(A 1, …, An)(R 2) makes R 1 be a relation with attributes A 1, …, An and the same tuples as R 2. u. Simplified notation: R 1(A 1, …, An) : = R 2. 23

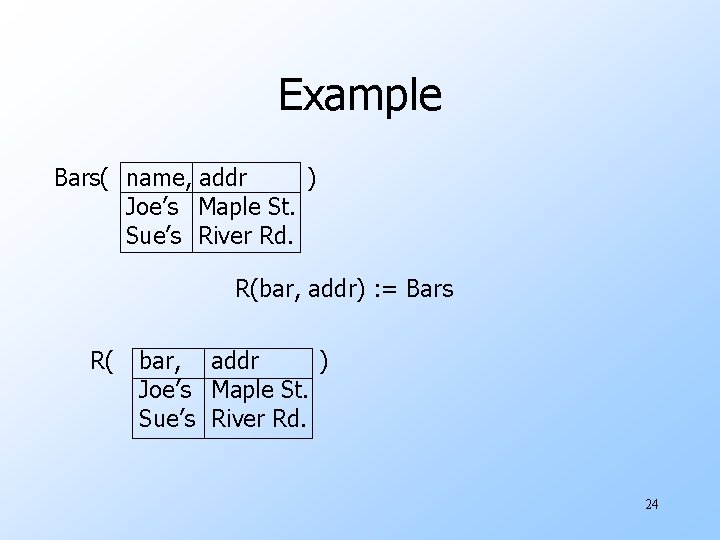
Example Bars( name, addr ) Joe’s Maple St. Sue’s River Rd. R(bar, addr) : = Bars R( bar, addr ) Joe’s Maple St. Sue’s River Rd. 24

RENAME u. Rename the attributes of a relation or change the relation name u. The general RENAME operation : w S (B 1, B 2, …, Bn )(R) changes both: • the relation name to S, and • the column (attribute) names to B 1, …. . Bn w S(R) changes: • the relation name only to S w (B 1, B 2, …, Bn )(R) changes: • the column (attribute) names only to B 1, …. . Bn

RENAME (shorthand) ushorthand for renaming attributes : R 1 FNAME, LNAME, SALARY (DEP 5_EMPS) R 1 has same attribute names as DEP 5_EMPS R 2 (F, L, S) ( FNAME, LNAME, SALARY (DEP 5_EMPS)) R 2 has attributes renamed to F, L and S R 3 (F, L, S) FNAME, LNAME, SALARY (DEP 5_EMPS) R 3 also has attributes renamed to F, L and S

Building Complex Expressions u Algebras allow us to express sequences of operations in a natural way. w Example: in arithmetic --- (x + 4)*(y - 3). u Relational algebra allows the same. u Three notations, just as in arithmetic: 1. Sequences of assignment statements. 2. Expressions with several operators. 3. Expression trees. 27

Sequences of Assignments u. Create temporary relation names. u. Renaming can be implied by giving relations a list of attributes. u. Example: R 3 : = R 1 JOINC R 2 can be written: R 4 : = R 1 * R 2 R 3 : = SELECTC (R 4) 28

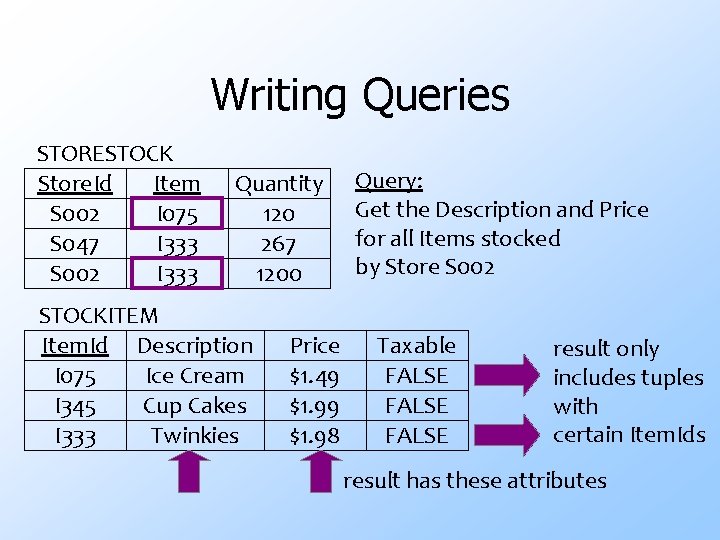
Writing Queries STORESTOCK Store. Id Item S 002 I 075 S 047 I 333 S 002 I 333 Quantity 120 267 1200 STOCKITEM Item. Id Description I 075 Ice Cream I 345 Cup Cakes I 333 Twinkies Price $1. 49 $1. 98 Query: Get the Description and Price for all Items stocked by Store S 002 Taxable FALSE result only includes tuples with certain Item. Ids result has these attributes

Writing Queries STORESTOCK Store. Id Item S 002 I 075 S 047 I 333 S 002 I 333 Quantity 120 267 1200 STOCKITEM Item. Id Description I 075 Ice Cream I 345 Cup Cakes I 333 Twinkies Price $1. 49 $1. 98 Query: Get the Description and Price for all Items stocked by Store S 002 We need a join to merge data across relations Taxable FALSE

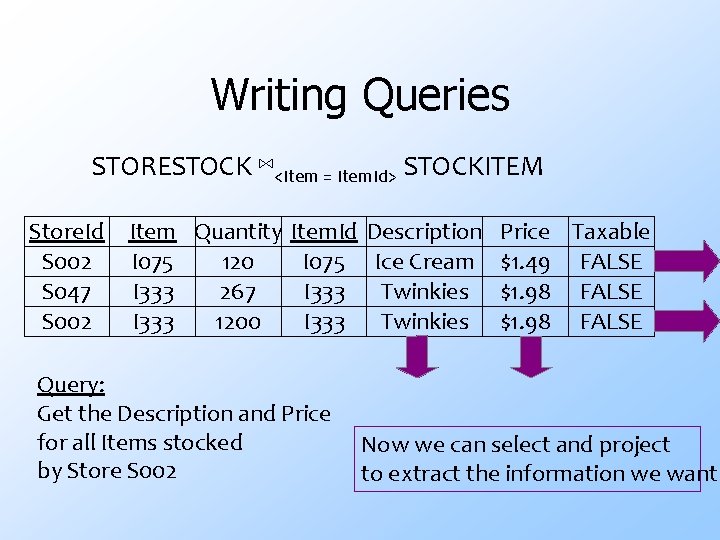
Writing Queries STORESTOCK ⋈<Item = Item. Id> STOCKITEM Store. Id S 002 S 047 S 002 Item Quantity Item. Id I 075 120 I 333 267 I 333 1200 Query: Get the Description and Price for all Items stocked by Store S 002 Description Ice Cream Twinkies Price Taxable $1. 49 FALSE $1. 98 FALSE Now we can select and project to extract the information we want

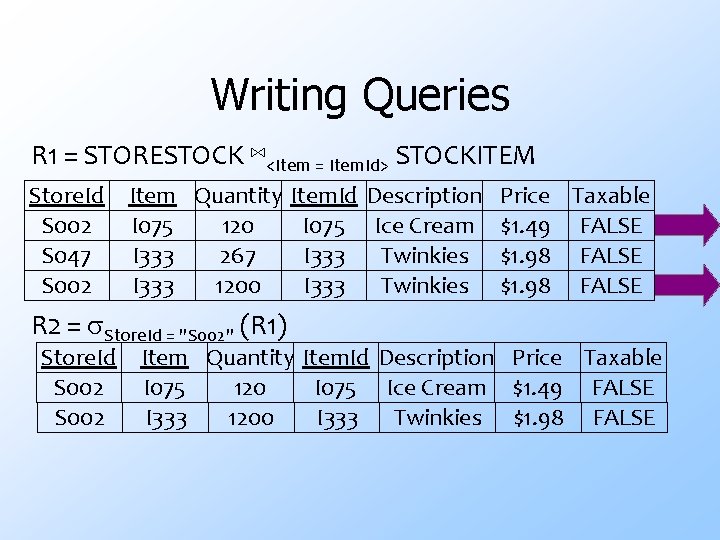
Writing Queries R 1 = STORESTOCK ⋈<Item = Item. Id> STOCKITEM Store. Id S 002 S 047 S 002 Item Quantity Item. Id I 075 120 I 333 267 I 333 1200 R 2 = Store. Id = "S 002" (R 1) Store. Id S 002 Description Ice Cream Twinkies Price Taxable $1. 49 FALSE $1. 98 FALSE Item Quantity Item. Id Description Price Taxable I 075 Ice Cream $1. 49 FALSE I 075 120 I 333 Twinkies $1. 98 FALSE I 333 1200

Writing Queries R 2 = Store. Id = "S 002" (R 1) Store. Id S 002 Item Quantity Item. Id Description Price Taxable I 075 Ice Cream $1. 49 FALSE I 075 120 I 333 Twinkies $1. 98 FALSE I 333 1200 R 3 = <Description, Price> (R 2) Description Price Ice Cream $1. 49 Twinkies $1. 98

Composing Queries Since the operands and results of every query are relations, we can compose or chain queries. R 1 = STORESTOCK ⋈<Item = Item. Id> STOCKITEM R 2 = Store. Id = "S 002" (R 1) R 3 = <Description, Price> (R 2) <Description, Price>( Store. Id = "S 002" (STORESTOCK ⋈<Item = Item. Id> STOCKITEM))

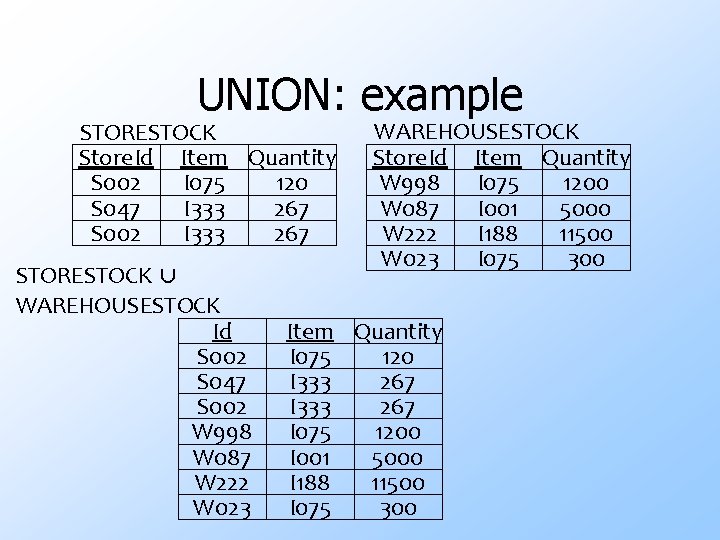
UNION: example STORESTOCK Store. Id Item Quantity S 002 I 075 120 S 047 I 333 267 S 002 I 333 267 STORESTOCK ⋃ WAREHOUSESTOCK Id S 002 S 047 S 002 W 998 W 087 W 222 W 023 WAREHOUSESTOCK Store. Id Item Quantity W 998 I 075 1200 W 087 I 001 5000 W 222 I 188 11500 W 023 I 075 300 Item Quantity I 075 120 I 333 267 I 075 1200 I 001 5000 I 188 11500 I 075 300

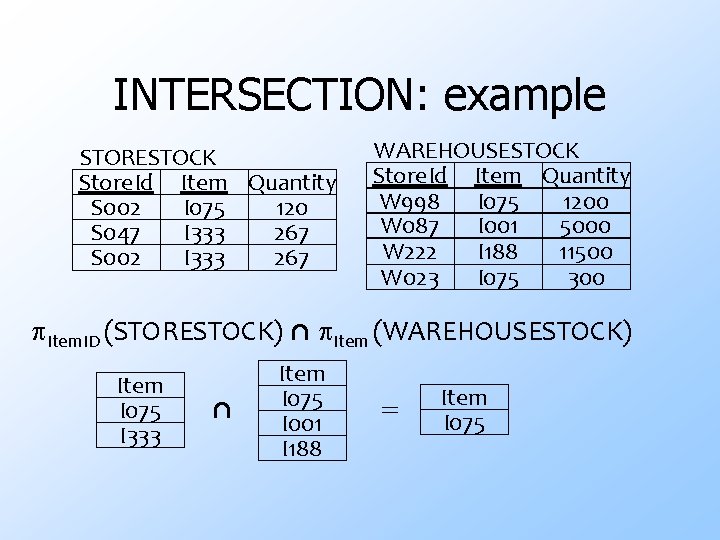
INTERSECTION: example STORESTOCK Store. Id Item Quantity S 002 I 075 120 S 047 I 333 267 S 002 I 333 267 WAREHOUSESTOCK Store. Id Item Quantity W 998 I 075 1200 5000 W 087 I 001 W 222 I 188 11500 W 023 I 075 300 Item. ID (STORESTOCK) ⋂ Item (WAREHOUSESTOCK) Item I 075 I 333 ⋂ Item I 075 I 001 I 188 = Item I 075

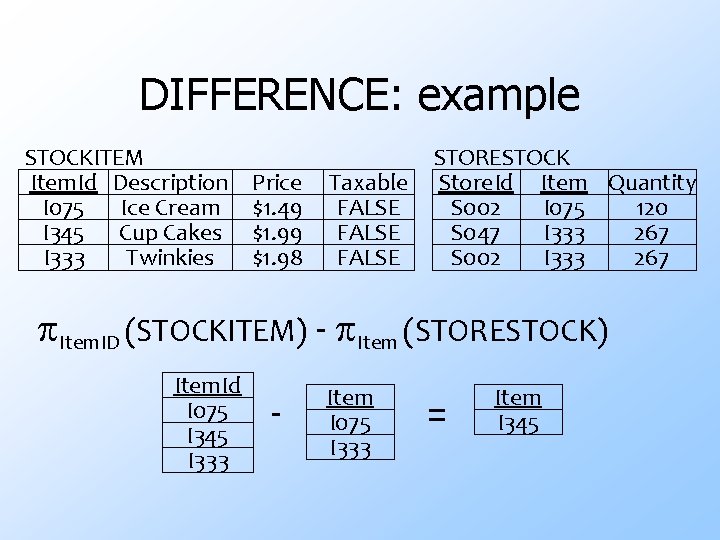
DIFFERENCE: example STOCKITEM Item. Id Description Price I 075 Ice Cream $1. 49 I 345 Cup Cakes $1. 99 I 333 Twinkies $1. 98 Taxable FALSE STORESTOCK Store. Id Item Quantity S 002 I 075 120 S 047 I 333 267 S 002 I 333 267 Item. ID (STOCKITEM) - Item (STORESTOCK) Item. Id I 075 I 345 I 333 - Item I 075 I 333 = Item I 345

Operator Precedence The normal way to group operators is: 1. Unary operators , , and have highest precedence. 2. Next highest are the “multiplicative” operators, and . , C 3. Lowest are the “additive” operators, , , and —. u But there is no universal agreement, so we always put parentheses around the argument of a unary operator, and it is a good idea to group all binary operators with parentheses enclosing their arguments. Example Group R S T as R ( (S ) T ). ,

Expression Trees u. Leaves are operands --- either variables standing for relations or particular, constant relations. u. Interior nodes are operators, applied to their child or children. 40

Example u. Using the relations Bars(name, addr) and Sells(bar, beer, price), find the names of all the bars that are either on Maple St. or sell Bud for less than $3. 41

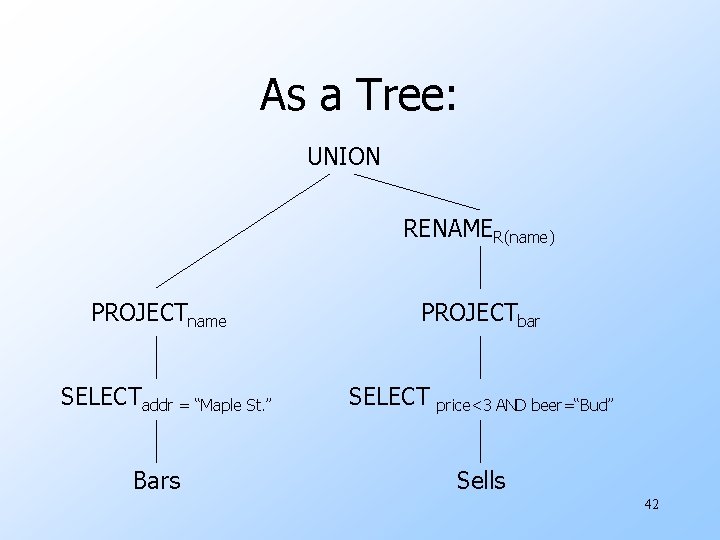
As a Tree: UNION RENAMER(name) PROJECTname SELECTaddr = “Maple St. ” Bars PROJECTbar SELECT price<3 AND beer=“Bud” Sells 42

Example u. Using Sells(bar, beer, price), find the bars that sell two different beers at the same price. u. Strategy: by renaming, define a copy of Sells, called S(bar, beer 1, price). The natural join of Sells and S consists of quadruples (bar, beer 1, price) such that the bar sells both beers at this price. 43

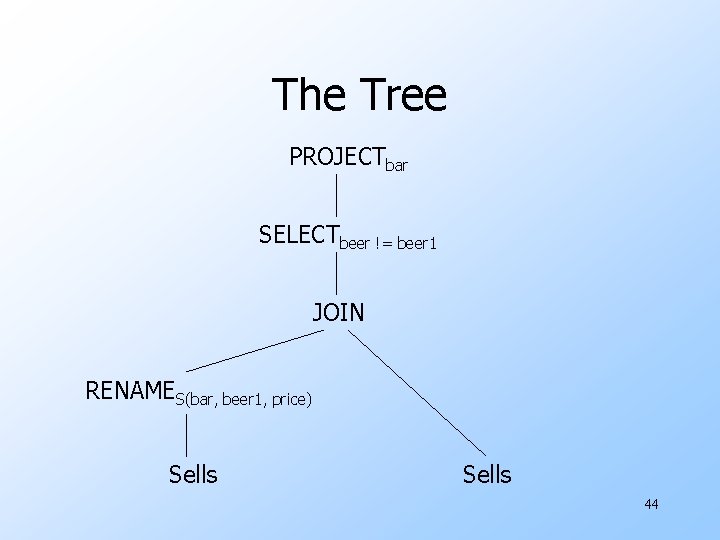
The Tree PROJECTbar SELECTbeer != beer 1 JOIN RENAMES(bar, beer 1, price) Sells 44

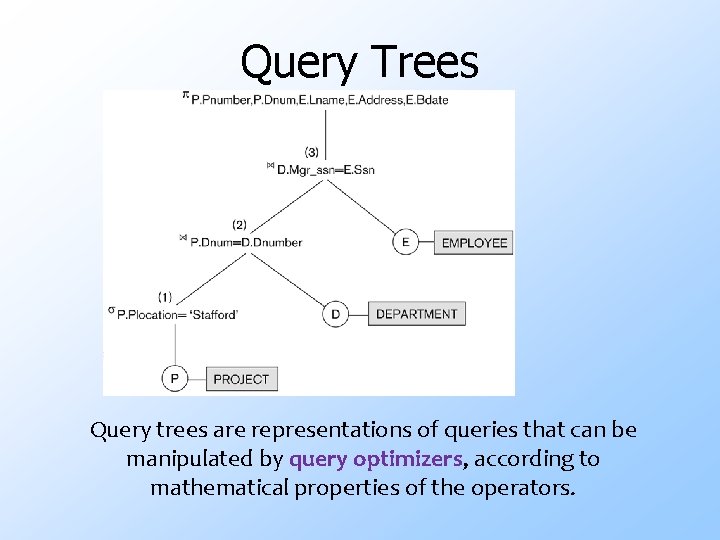
Query Trees Query trees are representations of queries that can be manipulated by query optimizers, according to mathematical properties of the operators.

Schema-Defining Rules 1 u. For union, intersection, and difference, the schemas of the two operands must be the same, so use that schema for the result. u. Selection: schema of the result is the same as the schema of the operand. u. Projection: list of attributes tells us the schema. 46

Schema-Defining Rules 2 u. Product: the schema is the attributes of both relations. w Use R. A, etc. , to distinguish two attributes named A. u. Theta-join: same as product. u. Natural join: use attributes of both relations. w Shared attribute names are merged. u. Renaming: the operator tells the schema. 47

Duplicate Elimination u. R 1 : = DELTA(R 2). u. R 1 consists of one copy of each tuple that appears in R 2 one or more times. 48

Example: Duplicate Elimination R= A 1 3 1 B 2 4 2 DELTA(R) = A 1 3 B 2 4 49

Sorting u. R 1 : = TAUL (R 2). w L is a list of some of the attributes of R 2. u. R 1 is the list of tuples of R 2 sorted first on the value of the first attribute on L, then on the second attribute of L, and so on. w Break ties arbitrarily. u. TAU is the only operator whose result is neither a set nor a bag. 50

Example: Sorting R= A 1 3 5 TAUB (R) = B 2 4 2 [(5, 2), (1, 2), (3, 4)] 51

Aggregation Operators u. Aggregation operators are not operators of relational algebra. u. Rather, they apply to entire columns of a table and produce a single result. u. The most important examples: SUM, AVG, COUNT, MIN, and MAX. 52

Example: Aggregation R= A 1 3 3 B 3 4 2 SUM(A) = 7 COUNT(A) = 3 MAX(B) = 4 AVG(B) = 3 53

Grouping Operator u R 1 : = GAMMAL (R 2). L is a list of elements that are either: 1. Individual (grouping ) attributes. 2. AGG(A ), where AGG is one of the aggregation operators and A is an attribute. 54

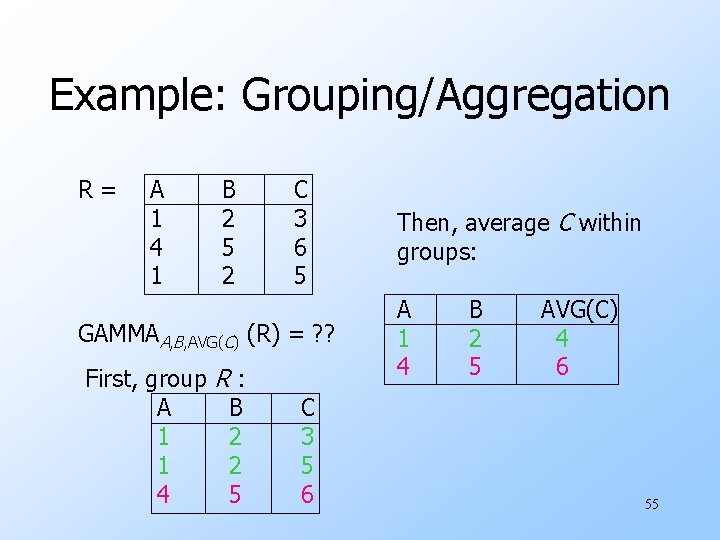
Example: Grouping/Aggregation R= A 1 4 1 B 2 5 2 C 3 6 5 GAMMAA, B, AVG(C) (R) = ? ? First, group A 1 1 4 R: B 2 2 5 C 3 5 6 Then, average C within groups: A 1 4 B 2 5 AVG(C) 4 6 55

EXERCISE 1: Queries Express the following queries in the algebra: 1. First and last name of employees who have no supervisor. 2. First and last name of employees supervised by Franklin Wong. 3. Last name of employees who have dependents. 4. Last name of employees who have daughters. 5. Last name of employees in department 5 who work more than 10 hours/week on Product. X. 6. Last name of supervisors of employees in department 5 who work more than 10 hours/week on Product. X.

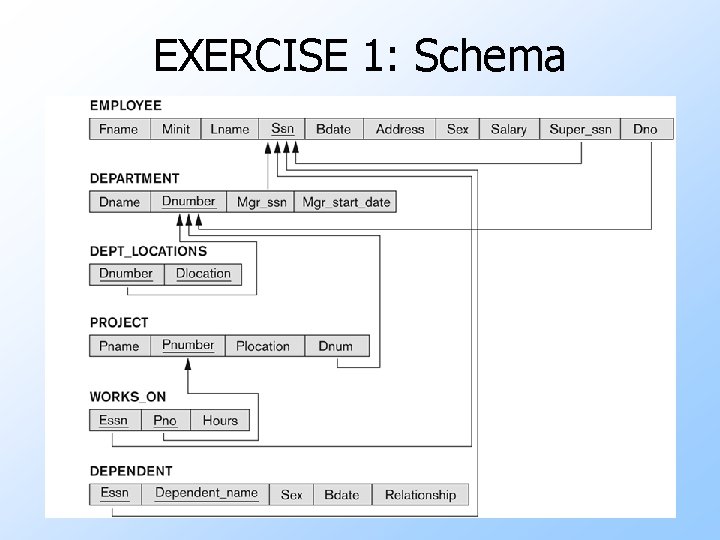
EXERCISE 1: Schema

EXERCISE 2: Queries 1. First and last names of all department managers. 2. Salaries of all employees who have worked on the Reorganization project. 3. SSN of all employees who have worked on a project that is controlled by a department different than the department that they are assigned to. 4. Last name of all employees who are not married.

Exercise 3: Schema

EXERCISE 3: Queries 1. List all airplane types that can land at any airport in San Francisco. 2. List the ids and number of seats for all airplanes that can land at any airport in Chicago. 3. List the name and phone number of all customers with a seat reserved on a flight that leaves Chicago O’Hara airport (ORD) on October 31, 2008. 4. List all airlines that have seats available for flights leaving Los Angeles (LAX) on September 25, 2008. 5. List all airlines that operate at San Jose International Airport (SJC).

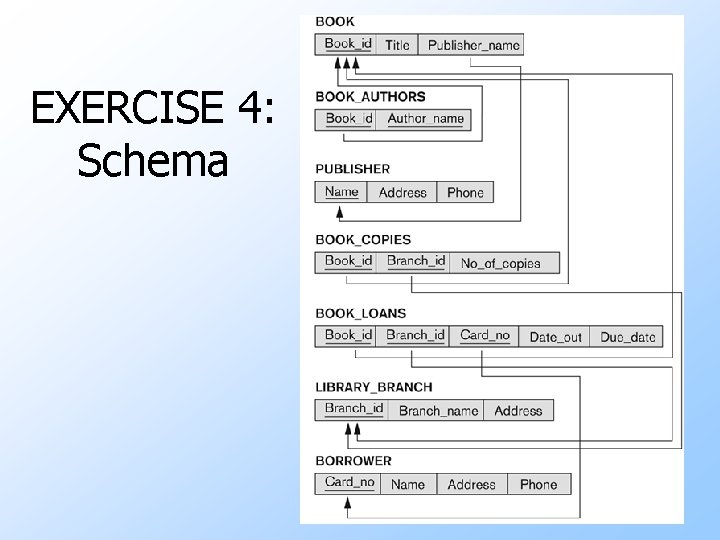
EXERCISE 4: Schema

EXERCISE 4: Queries 1. Count the number of overdue books. 2. How many books by author Harry Crews are in the database? 3. Determine the number of library cards assigned to each borrower phone number. 4. Find names of all borrowers who do not have any book loans. 5. Do any library branches have every book?