Relational Algebra Chapter 4 part I Relational Query

Relational Algebra Chapter 4 - part I

Relational Query Languages v Query languages: Allow manipulation and retrieval of data from a database. v Relational model supports simple, powerful QLs: § § v Strong formal foundation based on logic. Allows for much optimization. Query Languages != programming languages! § § § QLs not expected to be “Turing complete”. QLs not intended to be used for complex calculations. QLs support easy, efficient access to large data sets. 2

Formal Relational Query Languages Two mathematical Query Languages form the basis for “real” languages (e. g. SQL), and for implementation: q Relational Algebra: More operational, very useful for representing execution plans. · Relational Calculus: Lets users describe what they want, rather than how to compute it. (Nonoperational, rather declarative. ) q * Understanding Algebra & Calculus is key to * understanding SQL, query processing! 3

Preliminaries v A query is applied to relation instances, and the result of a query is also a relation instance. § Schemas of input relations for a query are fixed ; query will run regardless of instance!) § The schema for result of given query is also fixed! Determined by definition of query language. (but 4

Preliminaries v Positional vs. named-field notation: v Positional field notation e. g. , S. 1 v v Named field notation e. g. , S. sid Pros/Cons: § Positional notation easier formal definitions, namedfield notation more readable. § Both used in SQL v. Assume that names of fields in query results are `inherited’ from names of fields in query input relations. 5

Example Instances Sailors Reserves R 1 Sailors S 2 6

Relational Algebra v Basic operations: § § § v Additional operations: § v Selection ( ) Selects a subset of rows from relation. Projection ( ) Deletes unwanted columns from relation. Cartesian-product ( ) Allows us to combine two relations. Set-difference ( ) Tuples in reln. 1, but not in reln. 2. Union ( ) Tuples in reln. 1 and in reln. 2. Intersection, join, division, renaming: essential, but (very!) useful. Since each operation returns a relation, be composed! (Algebra is “closed”. ) Not operations can 7
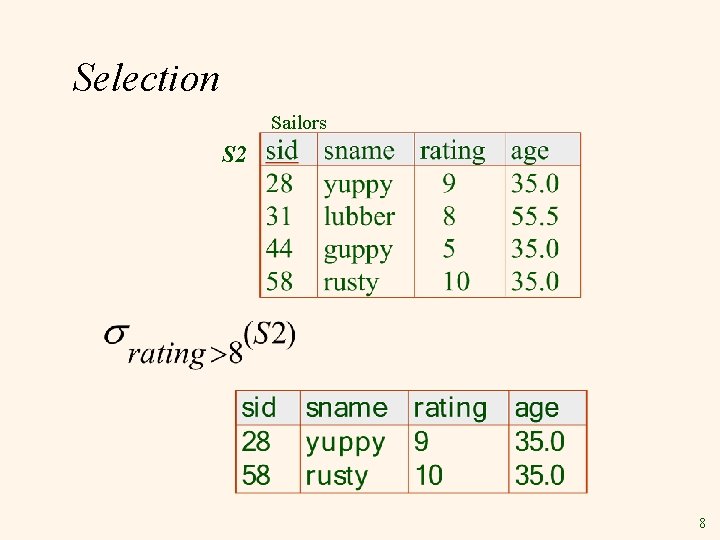
Selection Sailors S 2 8

Selection v v condition (R) Selects rows that satisfy selection condition. attribute op constant attribute op attribute Op is {<, >, <=, >=, =, =} v v No duplicates in result! Schema of result identical to schema of (only) input relation. 9
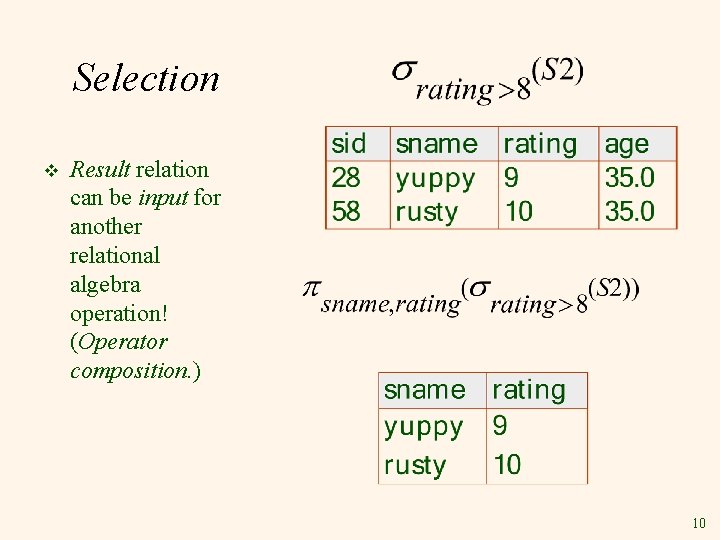
Selection v Result relation can be input for another relational algebra operation! (Operator composition. ) 10

Projection Sailors S 2 11

Projection v projectlist (R) v Deletes attributes that are not in projection list. Schema of result = contains fields in projection list Projection operator has to eliminate duplicates! (Why? ? ) § Note: real systems typically don’t do duplicate elimination unless the user explicitly asks for it. (Why not? ) v v 12

Union, Intersection, Set-Difference v All of these operations take two input relations, which must be union-compatible: § § v Same number of fields. `Corresponding’ fields have same type. What is the schema of result? 13
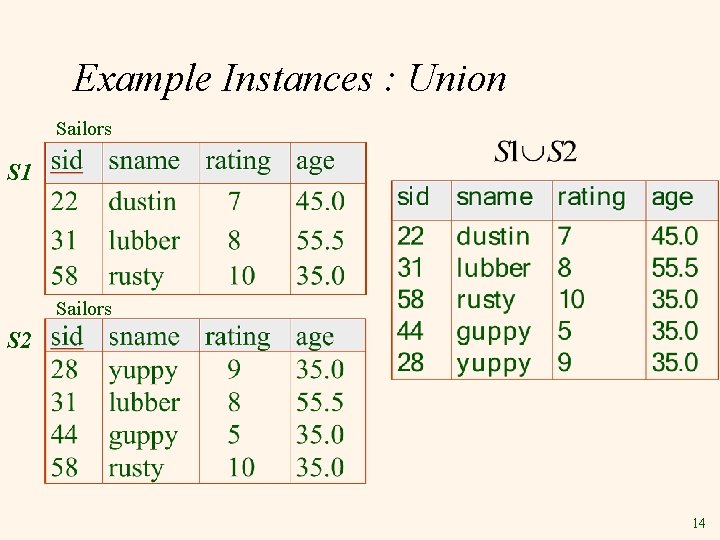
Example Instances : Union Sailors S 1 Sailors S 2 14
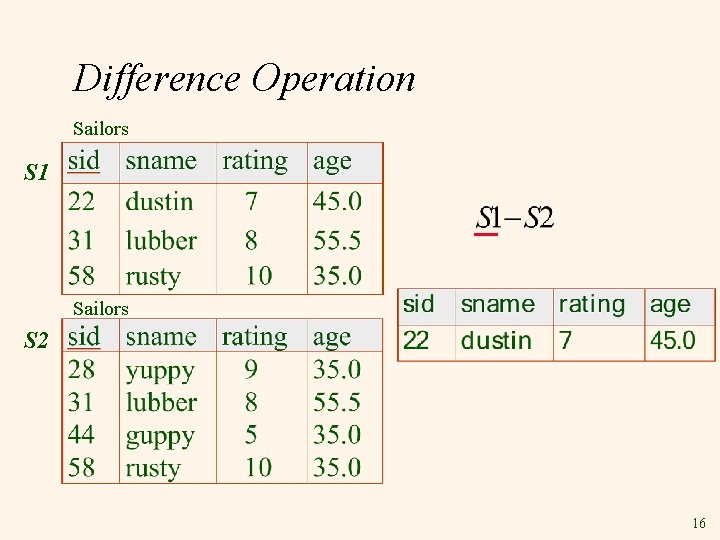
Difference Operation Sailors S 1 Sailors S 2 16

Intersection Operation Sailors S 1 Sailors S 2 18

Cross-Product (Cartesian Product) v v S 1 R 1 Each row of S 1 is paired with each row of R 1. Result schema has one field per field of S 1 and R 1, with field names `inherited’ if possible. § Conflict: Both S 1 and R 1 have a field called sid. * Renaming operator: 20

Joins (Why we need a Join? ) §In many cases, Join = Cross-Product + Select + Project § However : Cross-product is too large to materialize Apply Select and Project "On-the-fly" 21

Condition Join / Theta Join v Condition Join: v Result schema same as that of cross-product. Fewer tuples than cross-product, more efficient. v 22

Equi. Join v Equi-Join: A special case of condition join where the condition c contains only equalities. Result schema similar to cross-product, but only one copy of fields for which equality is specified. v An extra project v 23

Natural Join v Natural Join: Equijoin on all common fields. 24

Division v v Not supported as a primitive operator, but useful for expressing queries like: Find sailors who have reserved all boats. Let A have 2 fields x and y; B have only field y: § A/B = § i. e. , A/B contains all x tuples (sailors) such that for every y tuple (boat) in B, there is an xy tuple in A. § Or: If the set of y values (boats) associated with an x value (sailor) in A contains all y values in B, then x value is in A/B. 25

Division § A/B is the largest relation instance Q such that Q B A. e. g. , A = all parts supplied by suppliers, B= relation parts A/B = suppliers who supply all parts listed in B 26

Examples of Division A/B B 1 B 2 B 3 A A/B 1 A/B 2 A/B 3 27

Expressing A/B Using Basic Operators v Division is not essential op; just a useful shorthand. § v (Also true of joins, but joins are so common that systems implement joins specially. ) Idea: For A/B, compute all x values that are not `disqualified’ by some y value in B. § x value is disqualified if by attaching y value from B, we obtain an xy tuple that is not in A. Disqualified x values: A/B: all disqualified tuples 28

Find names of sailors who’ve reserved boat #103 Solution 1 Solution 2 Solution 3 29

Find names of sailors who’ve reserved a red boat v Information about boat color only available in Boats; so need an extra join: A more efficient solution: * A query optimizer can find this given the first solution! 30

Find sailors who’ve reserved a red or a green boat v Can identify all red or green boats, then find sailors who’ve reserved one of these boats: Can also define Tempboats using union! (How? ) What happens if is replaced by in this query? 31

Find sailors who’ve reserved a red and a green boat v Previous approach won’t work! Must identify sailors who’ve reserved red boats, sailors who’ve reserved green boats, then find the intersection (note that sid is a key for Sailors): 32

Find the names of sailors who’ve reserved all boats v Uses division; schemas of the input relations to / must be carefully chosen: v To find sailors who’ve reserved all ‘Interlake’ boats: . . . 33

Summary v The relational model has rigorously defined query languages that are simple and powerful. v Relational algebra is operational; useful as internal representation for query evaluation plans. v Several ways of expressing a given query; a query optimizer should choose most efficient version. 34

Example Instances Sailors S 1 Sailors S 2 35
- Slides: 32