Relation between Two Classes of Binary QuasiCyclic Goppa

Relation between Two Classes of Binary Quasi-Cyclic Goppa Codes Sergey Bezzateev and Natalia Shekhunova Saint Petersburg State University of Airspace Instrumentation Saint-Petersburg, Russia e-mail: bsv@aanet. ru, sna@delfa. net

Binary Goppa codes A binary vector a=(a 1, …an) of length n is a codeword of the Г(L, G) Goppa code if and only if G(x)- Goppa polynomial, L- locator set. Parameters of binary Goppa codes : Code length n ≤ 2 m Code dimension k≥n-m·deg. G(x) Minimal distance d≥deg. G(x)+1=dds.

Separable Binary Goppa codes G(x) is separable polynomial Minimal distance for separable binary Goppa codes d≥ 2 deg. G(x)+1=dds

Main questions To find codes with: • Improved estimations of parameters: dimension and minimal distance; • Good parameters (VG bound); • Special structure (large permutation group, quasi -cyclic, etc. ); • d=dds The binary separable codes with the location set L from GF(22 l) are of the greatest interest

Background M. Loeloeian and J. Conan (1984) presented (55, 16, 19) Goppa code G(x) = (x −α 9)(x − α 12)(x − α 30)(x − α 34)(x − α 42)(x − α 43)(x − α 50)(x − α 54) where α is a primitive element of GF(26). dds=17<d=19. We (1986) considered, G(x) = xt+1 + Vtxt + Vx + 1, “Subfield subcodes”, where L ⊂ GF(t 2), V ∈ {GF(t 2){1}} , n = t 2 − t − 1. k ≥ t 2 − t − 1 − 2 l(t − 3/2 ), where t=2 l. , dds=2 t+3. M. Loeloeian and J. Conan (1987), G(x) = xt + x, where L ⊂ GF(t 2) and n = t 2 − t. k ≥ t 2 − t − 2 l(t − 3/2 ) − 1, dds=2 t+1. A. M. Roseiro, J. I. Hall, J. E. Adney and M. Siegel (1992) By representation Gt(x) dds=2 t+1. = G(x) mod (xt 2+ x), k ≥ t 2 − t − 2 l(t − 3/2) − 1, We described(1995) G(x) = xt− 1 + 1, k ≥ t 2 − t − 2 l(t − 3/2 ), and we have proved that d=2 t-1.

Background P. Veron (2001) G(x) = xt + x - “Quadratic trace Goppa codes”. k = t 2 − t − 2 l(t − 3/2 ) − 1, d≥ 2 t+4 P. Veron (2005) G(x) = xt+1+Vtxt+Vx+1. k = t 2 − t − 1 − 2 l(t − 3/2) and G(x) = xt− 1 +1 , k= t 2 − t +1− 2 l(t − 3/2) -1 We (1995), P. Veron(1998), G. Bommer and F. Blanchet (2000) - all the forementioned codes are quasi-cyclic binary Goppa codes.

Two classes of quasi-cyclic Goppa codes Г(L; G(x)) and Г*(L*; G*(x)), where G(x) = xt-1 + 1; n=t 2 -t+1, k = t 2 - t - 2 l(t -3/2), d =dds=2 t - 1 G*(x) = xt+1 + 1; n*=t 2 -t-1, k* = t 2 - t - 2 l(t -3/2)-1, d* ≥dds=2 t + 3

CODEWORD STRUCTURE OF THE BINARY Г(L; G(x)) CODE It is easy to show that Г(L; G(x)) code is the quasi-cyclic code with the length of cycloid (t -1) and number of cycloids t. The codewords of this code have one fixed position – {0}. The total length of the code is n = t(t - 1) + 1

The numerators of the codewords of the Г(L; G(x)) code can be represented in the following form: L ={ βi, βi αt+1 , …, βi α(t+1)(t-2) } i=1, . . t U{0} where β = αt-1 , α is the primitive element of GF(22 l), and { βi, βi αt+1 , …, βi α(t+1)(t-2) } are numerators of positions that form the correspondent cycloids.

Transformation from Г(L; G(x)) to Г*(L*; G*(x)) G(x) = xt-1 +1 truncate G 1(x) = G (x), L 1 =L{0} Lemma 1 G 2(x) = x. G 1(x), L 2 =L 1 Theorem 2 (d 2=2 t+4) Substitution x-> x+ɣ , ɣt +ɣ +1 =0, ɣ∈GF(t 2) G 3(x) = xt +x+1, L 3 truncate G 3(x) = xt +x+1, L*3 = L 3 {0} Lemma 3 Substitution x -> x-1 G 4(x) = xt +xt-1 +1, L*4 Lemma 4 G 5(x) = x. G 4(x), L*5= L*4 Substitution x -> x+1 G 6(x) = xt+1 +1, L 6 G*(x) = xt+1 +1 Theorem 1 (d 2=2 t+3)

Transformation from Г(L; G(x)) to Г*(L*; G*(x)) G(x) = xt-1 +1 truncate G 1(x) = G (x), L 1 =L{0} Lemma 1 G 2(x) = x. G 1(x), L 2 =L 1 Theorem 2 (d 2=2 t+4) Substitution x-> x+ɣ , ɣt +ɣ +1 =0, ɣ∈GF(t 2) G 3(x) = xt +x+1, L 3 truncate G 3(x) = xt +x+1, L*3 = L 3 {0} Lemma 3 Substitution x -> x-1 G 4(x) = xt +xt-1 +1, L*4 Lemma 4 G 5(x) = x. G 4(x), L*5= L*4 Substitution x -> x+1 G 6(x) = xt+1 +1, L 6 G*(x) = xt+1 +1 Theorem 1 (d 2=2 t+3)

Г 1(L 1; G(x)) code obtained as trancated Г(L; G(x)) code by information position {0}, i. e. , we remove all codewords with 1 on position {0} from Г(L; G(x)) code. Then L 1 = L{0} and Г 1(L 1; G(x)) code is still quasi-cyclic code

Transformation from Г(L; G(x)) to Г*(L*; G*(x)) G(x) = xt-1 +1 truncate G 1(x) = G (x), L 1 =L{0} Lemma 1 G 2(x) = x. G 1(x), L 2 =L 1 Theorem 2 (d 2=2 t+4) Substitution x-> x+ɣ , ɣt +ɣ +1 =0, ɣ∈GF(t 2) G 3(x) = xt +x+1, L 3 truncate G 3(x) = xt +x+1, L*3 = L 3 {0} Lemma 3 Substitution x -> x-1 G 4(x) = xt +xt-1 +1, L*4 Lemma 4 G 5(x) = x. G 4(x), L*5= L*4 Substitution x -> x+1 G 6(x) = xt+1 +1, L 6 G*(x) = xt+1 +1 Theorem 1 (d 2=2 t+3)

It is possible to transform(Lemma 1) parity check matrix of the code Г 1(L 1; G(x)) to the a parity check matrix of the code Г 2(L 2; G 2(x)) where G 2(x) = xt + x , L 2 = L 1. This code still quasi-cyclic with the length of cycloid t -1 and the number of cycloids is t, n 2 = t(t - 1).

Transformation from Г(L; G(x)) to Г*(L*; G*(x)) G(x) = xt-1 +1 truncate G 1(x) = G (x), L 1 =L{0} Lemma 1 G 2(x) = x. G 1(x), L 2 =L 1 Theorem 2 (d 2=2 t+4) Substitution x-> x+ɣ , ɣt +ɣ +1 =0, ɣ∈GF(t 2) G 3(x) = xt +x+1, L 3 truncate G 3(x) = xt +x+1, L*3 = L 3 {0} Lemma 3 Substitution x -> x-1 G 4(x) = xt +xt-1 +1, L*4 Lemma 4 G 5(x) = x. G 4(x), L*5= L*4 Substitution x -> x+1 G 6(x) = xt+1 +1, L 6 G*(x) = xt+1 +1 Theorem 1 (d 2=2 t+3)

Let us consider now the following substitution: x -> z + ɣ , and ɣ t + ɣ +1 = 0, ɣ∈GF(t 2). Then G 2(x) = xt + x = zt + ɣ t + z + ɣ = zt + z + 1 = G 3(z).

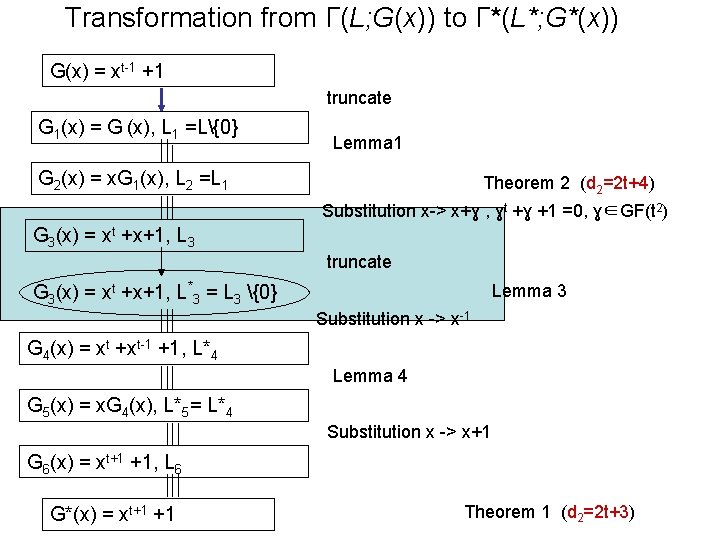
Transformation from Г(L; G(x)) to Г*(L*; G*(x)) G(x) = xt-1 +1 truncate G 1(x) = G (x), L 1 =L{0} Lemma 1 G 2(x) = x. G 1(x), L 2 =L 1 Theorem 2 (d 2=2 t+4) Substitution x-> x+ɣ , ɣt +ɣ +1 =0, ɣ∈GF(t 2) G 3(x) = xt +x+1, L 3 truncate G 3(x) = xt +x+1, L*3 = L 3 {0} Lemma 3 Substitution x -> x-1 G 4(x) = xt +xt-1 +1, L*4 Lemma 4 G 5(x) = x. G 4(x), L*5= L*4 Substitution x -> x+1 G 6(x) = xt+1 +1, L 6 G*(x) = xt+1 +1 Theorem 1 (d 2=2 t+3)

The code Г 3(L 3; G 3(x)) has parameters n 3 = t(t - 1); k 3 = k 2 = k 1 – 1; d 3 = 2 t + 4

Let us consider now Г*3(L*3 ; G 3(x)) code obtained from Г 3(L 3 ; G 3(x))-code by trancation on position {0}, i. e. , L*3 = L 3{0}: This code has parameters: n*3 = n 3 - 1; k*3 = k 2 = k 1 - 1; d*3 = d 3 - 1 = d 2 - 1 = 2 t + 3:

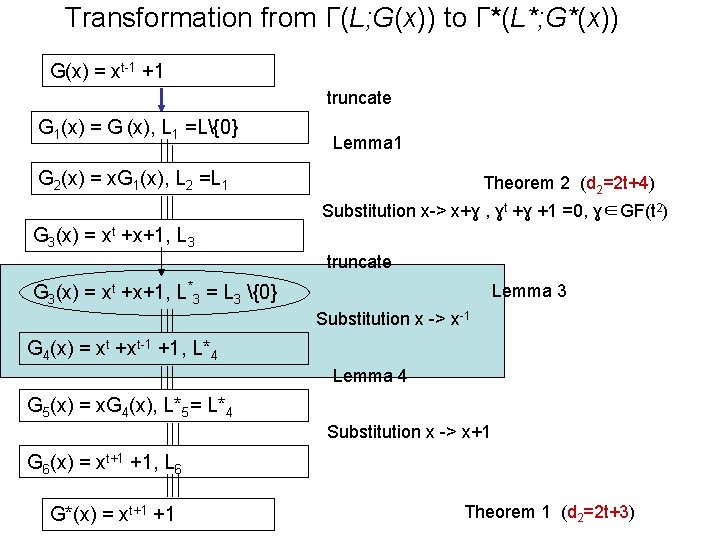
Transformation from Г(L; G(x)) to Г*(L*; G*(x)) G(x) = xt-1 +1 truncate G 1(x) = G (x), L 1 =L{0} Lemma 1 G 2(x) = x. G 1(x), L 2 =L 1 Theorem 2 (d 2=2 t+4) Substitution x-> x+ɣ , ɣt +ɣ +1 =0, ɣ∈GF(t 2) G 3(x) = xt +x+1, L 3 truncate G 3(x) = xt +x+1, L*3 = L 3 {0} Lemma 3 Substitution x -> x-1 G 4(x) = xt +xt-1 +1, L*4 Lemma 4 G 5(x) = x. G 4(x), L*5= L*4 Substitution x -> x+1 G 6(x) = xt+1 +1, L 6 G*(x) = xt+1 +1 Theorem 1 (d 2=2 t+3)

Now let us use the following substitution: z -> y -1. Then G 3(z) = zt + z + 1 = y-t + y-1 + 1 -> G 4(y) = yt + yt-1 + 1. Code Г 4(L*4; G 4(x)) has parameters n*4 = n*3 = n 3 - 1; k*4 = k*3 ; d*4 = d 3 - 1:

Transformation from Г(L; G(x)) to Г*(L*; G*(x)) G(x) = xt-1 +1 truncate G 1(x) = G (x), L 1 =L{0} Lemma 1 G 2(x) = x. G 1(x), L 2 =L 1 Theorem 2 (d 2=2 t+4) Substitution x-> x+ɣ , ɣt +ɣ +1 =0, ɣ∈GF(t 2) G 3(x) = xt +x+1, L 3 truncate G 3(x) = xt +x+1, L*3 = L 3 {0} Lemma 3 Substitution x -> x-1 G 4(x) = xt +xt-1 +1, L*4 Lemma 4 G 5(x) = x. G 4(x), L*5= L*4 Substitution x -> x+1 G 6(x) = xt+1 +1, L 6 G*(x) = xt+1 +1 Theorem 1 (d 2=2 t+3)

Lemma 4 Code Г*4 (L*4 ; G 4(x)) ≡ Г*5(L*5 ; G 5(x)); where G 5(y) = y. G 4(y) = yt+1+yt+y and L*5 = L*4.

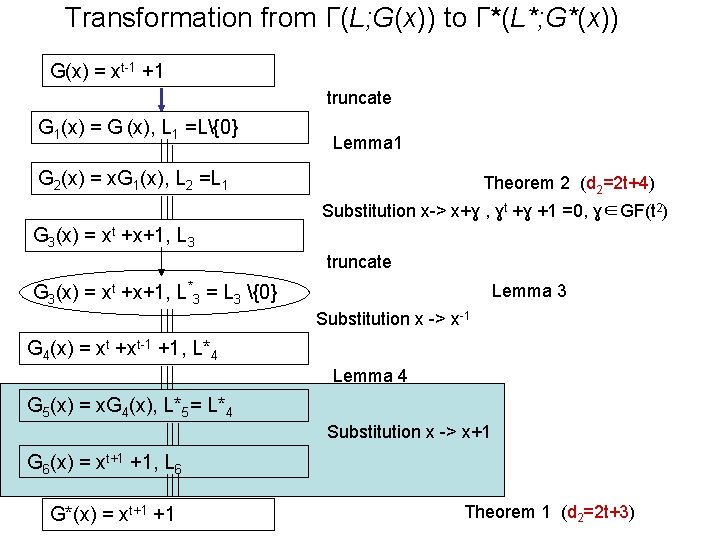
Transformation from Г(L; G(x)) to Г*(L*; G*(x)) G(x) = xt-1 +1 truncate G 1(x) = G (x), L 1 =L{0} Lemma 1 G 2(x) = x. G 1(x), L 2 =L 1 Theorem 2 (d 2=2 t+4) Substitution x-> x+ɣ , ɣt +ɣ +1 =0, ɣ∈GF(t 2) G 3(x) = xt +x+1, L 3 truncate G 3(x) = xt +x+1, L*3 = L 3 {0} Lemma 3 Substitution x -> x-1 G 4(x) = xt +xt-1 +1, L*4 Lemma 4 G 5(x) = x. G 4(x), L*5= L*4 Substitution x -> x+1 G 6(x) = xt+1 +1, L 6 G*(x) = xt+1 +1 Theorem 1 (d 2=2 t+3)

Let us use the following substitution: y -> u + 1; then G 5(y) = yt+1 + yt + y -> (u + 1)t+1 + (u + 1)t + u = ut+1 + 1 = G 6(u)=G*(u).

Г*(L*; G*(x)) codes have the following parameters: n* = n*4 = n 3 -1 = t(t - 1) - 1; k* = k*4 = k*3 = k - 1; Theorem 1 The minimal distance of Г*(L*; G*(x)) code is d* = 2 t + 3 Theorem 2 The minimal distance of Г 2(L 2; G 2(x)) code is d 2 = 2 t + 4 and number of information symbols is k 2 = k 1 - 1. d 2 = d 3 =d*3 + 1 = d* +1=2 t + 4:

Code’s parameters code length code dimension G (x) = xt-1 +1 t 2 –t+1 =t 2 –t-2 l(t-3/2) minimal distance =2 t-1 (P. Veron, 2005) G 2(x)=xt +x t 2 –t G* (x) = xt+1 +1 t 2 –t-1 =t 2 –t-1 -2 l(t-3/2) =2 t+4 (P. Veron, 2001) =t 2 –t-1 -2 l(t-3/2) =2 t+3 (P. Veron, 2005) G 4(x)=xt +xt-1 +1 t 2 –t (t 2 –t-1) =t 2 –t-1 -2 l(t-3/2) =2 t+3

THANK YOU FOR YOUR ATTENTION!

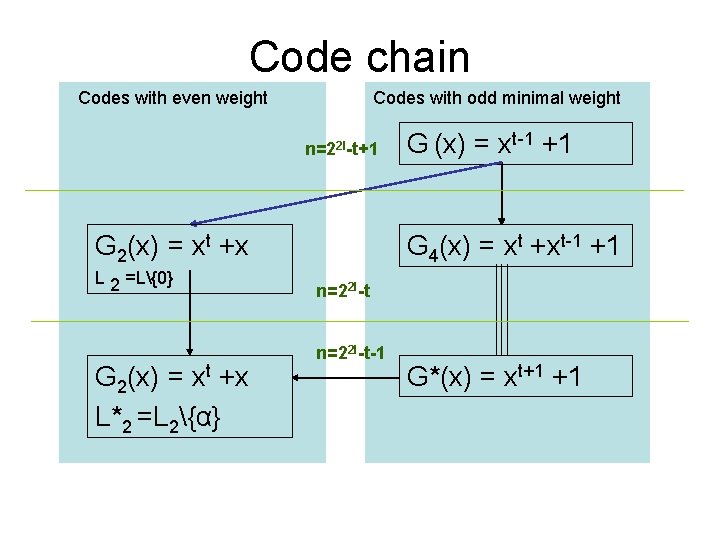
Code chain Codes with even weight Codes with odd minimal weight n=22 l-t+1 G 2(x) = xt +x L 2 =L{0} G 2(x) = xt +x L*2 =L 2{α} G (x) = xt-1 +1 G 4(x) = xt +xt-1 +1 n=22 l-t-1 G*(x) = xt+1 +1