RELASI Definisi dan Notasi Relasi R dari A

RELASI

Definisi dan Notasi: Relasi R dari A ke B merupakan sub-himpunan dari A B R: A B Representasi dari relasi R : A B, bisa dilakukan dg 4 cara: 1) himpunan pasangan terurut, 2) pemetaan, 3) matriks, 4) Notasi Digunakan matriks dengan : • baris merepresentasikan elemen-elemen A • kolom merepresentasikan elemen-elemen B • entri (ai, bj) = 1 jika (ai, bj) R, i, j menunjukkan indeks • entri (ai, bj) = 0 jika (ai, bj) R

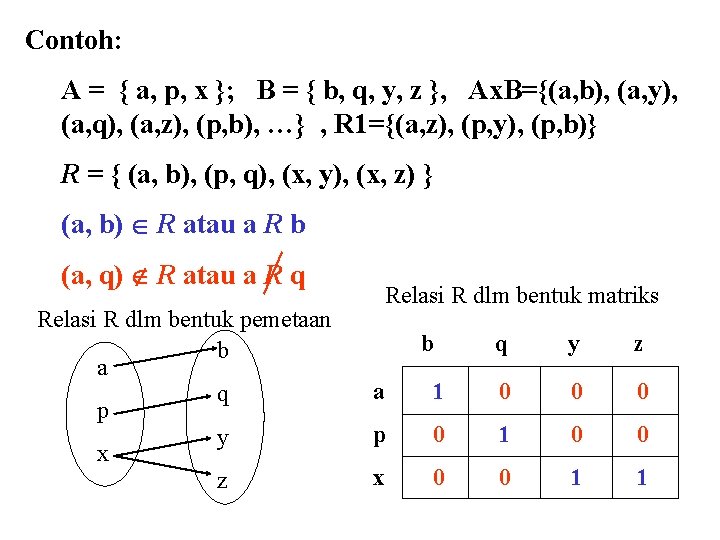
Contoh: A = { a, p, x }; B = { b, q, y, z }, Ax. B={(a, b), (a, y), (a, q), (a, z), (p, b), …} , R 1={(a, z), (p, y), (p, b)} R = { (a, b), (p, q), (x, y), (x, z) } (a, b) R atau a R b (a, q) R atau a R q Relasi R dlm bentuk pemetaan b a q p y x z Relasi R dlm bentuk matriks b q y z a 1 0 0 0 p 0 1 0 0 x 0 0 1 1

Invers dari relasi R (R– 1), R– 1 : B A R– 1 = { (b, a) | (a, b) R} = { (b, a), (q, p), (y, x), (z, x) } Komplemen dari relasi R, R : A B R = { (a, b | (a, b) R , tapi (a, b) AXB} = { (a, q), (a, y), (a, z), (p, b), (p, y), (p, z), (x, b), (x, q) } Tentukan himp relasi yang unsur absisnya huruf vokal dan ordinatnya huruf konsonan dari A dan B di atas!

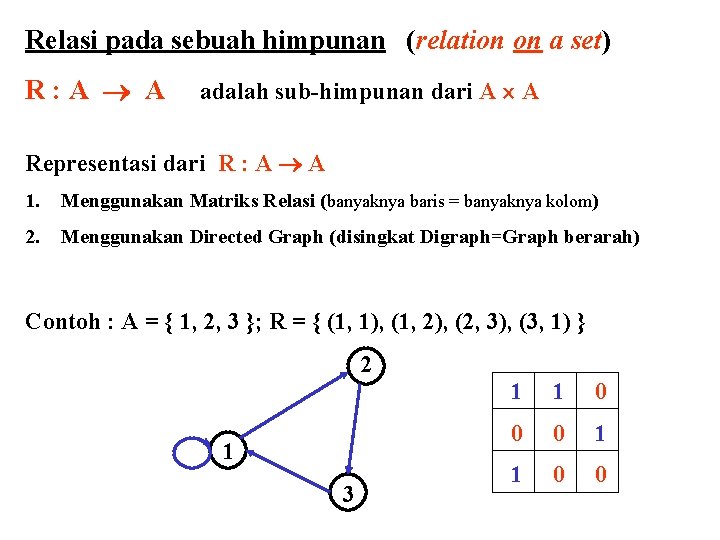
Relasi pada sebuah himpunan (relation on a set) R: A A adalah sub-himpunan dari A A Contoh (Example 5): R : Bil Bulat R 1 = { (a, b) | a b} R 2 = { (a, b) | a b} R 3 = { (a, b) | a = b or a = – b } R 4 = { (a, b) | a = b} R 5 = { (a, b) | a = b + 1 } R 6 = { (a, b) | a + b 3}

Relasi pada sebuah himpunan (relation on a set) R: A A adalah sub-himpunan dari A A Representasi dari R : A A 1. Menggunakan Matriks Relasi (banyaknya baris = banyaknya kolom) 2. Menggunakan Directed Graph (disingkat Digraph=Graph berarah) Contoh : A = { 1, 2, 3 }; R = { (1, 1), (1, 2), (2, 3), (3, 1) } 2 1 3 1 1 0 0 0 1 1 0 0

Sifat-sifat relasi R : A A 1. Refleksif : a [ (a, a) R ] 2. Irefleksif : a [ (a, a) R ] Sifat-sifat relasi R : A B 1. Simetrik : a, b [ (a, b) R (b, a) R ] 2. Antisimetrik : a, b [ ((a, b) R (b, a) R) (a = b) ] atau a , b [ (a b) ((a, b) R (b, a) R) ] 3. Transitif: a, b, c [((a, b) R (b, c) R) (a, c) R ] 4. Asimetrik : a, b [ (a, b) R (b, a) R ]

Contoh (Example 5): Cek sifat-sifat relasi R : A A , di mana A = { 1, 2, 3, 4 } R 1 = { (a, b) | a b} R 4 = { (a, b) | a = b} R 2 = { (a, b) | a b} R 5 = { (a, b) | a = b + 1 } R 3 = { (a, b) | a = b or a = – b } R 6 = { (a, b) | a + b 3} R 1 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)} Refleksif : ya, karena(1, 1), (2, 2), (3, 3), (4, 4) R 1 Irefleksif : tidak, karena (1, 1) R 1 Simetrik : tidak, karena (1, 3) R 1 (3, 1) R 1 Asimetrik : ya, karena (4 a, 4 b) R 1 (4 b, 4 a) R 1 Antisimetrik : ya, karena [(4 a, 4 b) R 1 (4 b, 4 a) R 1] ( 4 a = 4 b ) memenuhi untuk (1, 1), (2, 2), (3, 3) juga

Contoh (Example 5): Cek sifat-sifat relasi R : A A , di mana A = { 1, 2, 3 } R 2 = { (a, b) | a b} R 5 = { (a, b) | a = b + 1 } R 6 = { (a, b) | a + b 3} Periksa sifat relasi utk relasi tsb Kerjakan per kelompok maks 3 org Sekarang!

R 1 : { 1, 2, 3, 4 }, A di mana R 1 = { (a, b) | a b} R 1 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)} Transitif : (a, b) R 1 dan (b, c) R 1 (a, c) R 1 (1, 1) R 1 dan (1, 1) R 1 ; (1, 1) R 1 dan (1, 2) R 1 (1, 1) R 1 dan (1, 3) R 1 ; (1, 1) R 1 dan (1, 4) R 1 (1, 2) R 1 dan (2, 2) R 1 (1, 2) R 1 ; (1, 2) R 1 dan (2, 3) R 1 (1, 3) R 1 (1, 2) R 1 dan (2, 4) R 1 (1, 4) R 1 ; (1, 3) R 1 dan (3, 3) R 1 (1, 3) R 1 dan (3, 4) R 1 (1, 4) R 1 ; (1, 4) R 1 dan (4, 4) R 1 (1, 4) R 1 (2, 2) R 1 dan (2, 2) R 1 ; (2, 2) R 1 dan (2, 3) R 1 (2, 2) R 1 dan (2, 4) R 1; (2, 3) R 1 dan (3, 3) R 1 (2, 3) R 1 dan (3, 4) R 1 (2, 4) R 1; (2, 4) R 1 dan (4, 4) R 1 (2, 4) R 1 (3, 3) R 1 dan (3, 3) R 1 ; (3, 3) R 1 dan (3, 4) R 1 (4, 4) R 1 dan (4, 4) R 1

1. Refleksif: a [ (a, a) R ] R : integer R 1 = { (a, b) | a b} ya R 2 = { (a, b) | a b} tidak R 3 = { (a, b) | a = b or a = – b } ya R 4 = { (a, b) | a = b} ya R 5 = { (a, b) | a = b + 1 } tidak R 6 = { (a, b) | a + b 3 } ya

2. Simetrik: a b [ (a, b) R (b, a) R ] R : integer R 1 = { (a, b) | a b} tidak R 2 = { (a, b) | a b} tidak R 3 = { (a, b) | a = b or a = – b } ya R 4 = { (a, b) | a = b} ya R 5 = { (a, b) | a = b + 1 } tidak R 6 = { (a, b) | a + b 3 } ya

3. Antisimetrik : a b [ ((a, b) R (b, a) R) (a = b) ] atau a b [ (a b) ((a, b) R (b, a) R) ] R : integer R 1 = { (a, b) | a b} R 2 = { (a, b) | a b} R 3 = { (a, b) | a = b or a = – b } R 4 = { (a, b) | a = b} R 5 = { (a, b) | a = b + 1 } R 6 = { (a, b) | a + b 3 }

4. Transitif : a b c [((a, b) R (b, c) R) (a, c) R ] R : integer R 1 = { (a, b) | a b} R 2 = { (a, b) | a b} R 3 = { (a, b) | a = b or a = – b } R 4 = { (a, b) | a = b} R 5 = { (a, b) | a = b + 1 } R 6 = { (a, b) | a + b 3 }

5. Irefleksif : a [ (a, a) R ] R : integer R 1 = { (a, b) | a b} R 2 = { (a, b) | a b} R 3 = { (a, b) | a = b or a = – b } R 4 = { (a, b) | a = b} R 5 = { (a, b) | a = b + 1 } R 6 = { (a, b) | a + b 3 }

6. Asimetrik : a b [ (a, b) R (b, a) R ] R : integer R 1 = { (a, b) | a b} R 2 = { (a, b) | a b} R 3 = { (a, b) | a = b or a = – b } R 4 = { (a, b) | a = b} R 5 = { (a, b) | a = b + 1 } R 6 = { (a, b) | a + b 3 }

SOAL: Periksa ke-6 sifat relasi untuk (1) Relasi invers dari R 1 s/d. R 6 (2) Relasi komplementer dari R 1 s/d. R 6 Catatan: R: A B Relasi invers dari R, notasi R-1: B A { (b, a) | (a, b) R } Relasi komplemen dari R, notasi R: A B { (a, b) | (a, b) R }

Kombinasi dua relasi: R 1 : A B R 2 : A B 1. R 1 R 2 2. R 1 R 2 3. R 1 R 2 4. R 1 – R 2 5. R 2 – R 1 Catatan: baca Examples 3, 4 (halaman 491, 492)

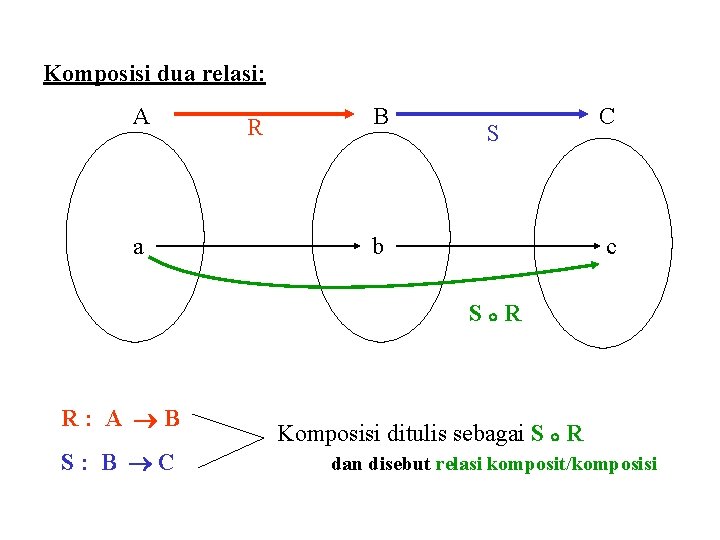
Komposisi dua relasi: A a R B S b C c S R R: A B S: B C Komposisi ditulis sebagai S R dan disebut relasi komposit/komposisi

Contoh: R : A B di mana A = { 1, 2, 3 } dan B = { 1, 2, 3, 4 } S: B C di mana C = { 0, 1, 2 } R = { (1, 1), (1, 4), (2, 3), (3, 1), (3, 4) } S = { (1, 0), (2, 0), (3, 1), (3, 2), (4, 1) } S R = ………………. Soal: Gambarkan relasi komposit tersebut.

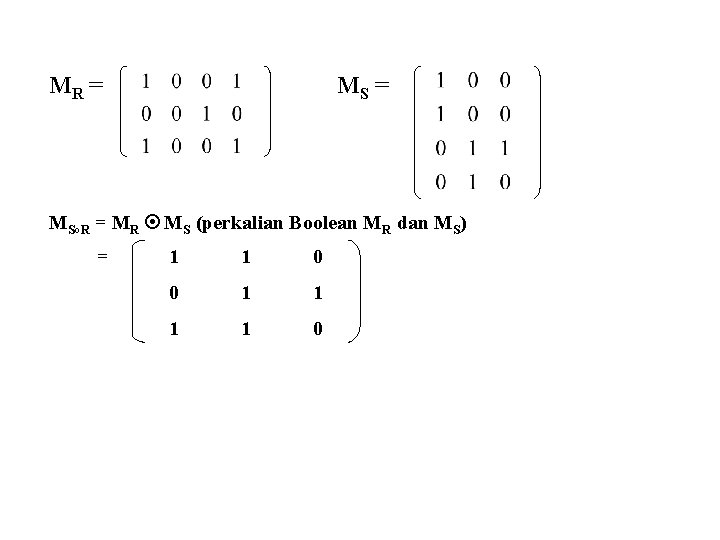
Representasi relasi komposit: R : A B di mana A = { 1, 2, 3 } dan B = { 1, 2, 3, 4 } S: B C di mana C = { 0, 1, 2 } R = { (1, 1), (1, 4), (2, 3), (3, 1), (3, 4) } S = { (1, 0), (2, 0), (3, 1), (3, 2), (4, 1) } MR = MS°R = MR MS (perkalian Boolean MR dan MS)

MR = MS°R = MR MS (perkalian Boolean MR dan MS) = 1 1 0 0 1 1 0

Komposisi lebih dari dua relasi R: A A R 1 = R R 2 = R R R 3 = R 2 R ………. Rn+1 = Rn R

Contoh: R : {1, 2, 3, 4} R = { (1, 1), (2, 1), (3, 2), (4, 3) } R 2 = { (1, 1), (2, 1), (3, 1), (4, 2) } R 3 = { (1, 1), (2, 1), (3, 1), (4, 1) } R 4 = { (1, 1), (2, 1), (3, 1), (4, 1) } R 5 = { (1, 1), (2, 1), (3, 1), (4, 1) } dst Soal: Verifikasi dengan gambar

RELASI n-ary Sub-bab 7. 2

Relasi R: Binary : (a 1, a 2) disebut ordered-pair Contoh : (Nama_mahasiswa, nilai_UTS) Ternary : (a 1, a 2, a 3) disebut ordered-triple Contoh : (NRP_mhs, Nama_mhs, nilai_UTS) Contoh lain: R adalah relasi (penerbangan, no-penerbangan, asal, tujuan, waktu-berangkat) Disebut quintuple (karena terdiri dari 5 komponen) n-ary : (a 1, a 2, a 3, … , an) disebut n-tuple

Relasi R: Binary : (a 1, a 2) disebut ordered-pair Contoh : (Nama_mahasiswa, nilai_UTS) Ternary : (a 1, a 2, a 3) disebut ordered-triple Contoh : (NRP_mhs, Nama_mhs, nilai_UTS) Contoh lain: R adalah relasi (penerbangan, no-penerbangan, asal, tujuan, waktu-berangkat) Disebut quintuple (karena terdiri dari 5 komponen) n-ary : (a 1, a 2, a 3, … , an) disebut n-tuple

Definisi: Relasi n-ary adalah sub-himpunan dari A 1 A 2 A 3 … An Himpunan-himpunan A 1, A 2, A 3, …, An disebut domain dari relasi n disebut derajat relasi Aplikasi: Basis Data Relasional

Terminologi: Tabel : alternatif representasi basis data relasional Primary-key : a domain of an n-ary relation such that an n-tuple is uniquely determined by its value for this domain Composite-key : the Cartesian product of domains of an n-ary relation such that an n-tuple is uniquely determined by its values for these domains Projection : a function that produces relations of smaller degree from an n-ary relation by deleting fields Join : a function that combines n-ary relations that agree on certain fields SQL : Structured Query Language

Primary-key : a domain of an n-ary relation such that an n-tuple is uniquely determined by its value for this domain Contoh: lihat Tabel 1 4 -tuple : (nama, nomor-identitas, jurusan, IPK) (Ackermann, 231455, CS, 3. 88) (Adams, 8888323, Physics, 3. 45) (Chou, 102147, CS, 3. 49) (Goodfriend, 453876, Math, 3. 45) (Rao, 678543, Math, 3. 90) (Stevens, 786576, Psychology, 2. 99) Alternatif primary-key: nama, nomor-identitas

Composite-key : the Cartesian product of domains of an n-ary relation such that an n-tuple is uniquely determined by its values for these domains Contoh: 4 -tuple : (nama, nomor-identitas, jurusan, IPK) (Ackermann, 231455, CS, 3. 88) CS, 3. 45 (Adams, 8888323, Physics, 3. 45) CS, 3. 88 (Chou, 102147, CS, 3. 49) Math, 3. 45 (Goodfriend, 453876, Math, 3. 45) Math, 3. 90 (Rao, 678543, Math, 3. 90) Physics, 3. 45 (Stevens, 786576, Psychology, 2. 99) Psychology, 2. 99 Alternatif composite-key: jurusan x IPK

Projection : a function that produces relations of smaller degree from an n-ary relation by deleting fields Pi 1, i 2, i 3, … , im deletes n–m of the components of the n-tuple, leaving the i 1 th, i 2 th, i 3 th, …, imth components Lihat Example 7

Join : Jp Jp is a function that combines all m-tuples of the first relation with all n-tuples of the second relation, where the last p components of the m-tuples agree with the first p components of the n-tuples. Lihat Example 9 halaman 486