RELACIONES DE EQUIVALENCIA Las relaciones de equivalencia Qu

RELACIONES DE EQUIVALENCIA

Las relaciones de equivalencia: ¿Qué son? Congruencias ¿Por qué son importantes? Ejemplos Ejercicios Mapa conceptual y definiciones

¿Por qué son importantes las relaciones de equivalencia? Porque clasifican a los elementos del conjunto donde están definidas según un atributo (es decir según las condiciones que deben cumplir los elementos que se relacionan).

Ejemplos 1. Sea el conjunto de todos los seres humanos y la relación: “tiene la misma fecha de cumpleaños que”. 2. Sea el conjunto del parque automotor y la relación: “ es del mismo color que”. 3. Sea R la relación en el conjunto de todas las personas que han visitado una página web determinada, tal que a. Rb la persona a y la persona b, han seguido el mismo conjunto de enlaces a partir de esta página web (yendo de una página web a otra hasta que se desconectan de Internet).

¿ Qué es una relación de equivalencia? Las relaciones de equivalencia son relaciones entre los elementos de un conjunto cualquiera y su característica principal es que abstraen el concepto de igualdad. Es una relación definida en un conjunto que cumple con las propiedades reflexiva, simétrica y transitiva.

Propiedad Reflexiva: Una relación R sobre un conjunto X recibe el nombre de reflexiva si x X: (x; x) R. Observaciones para conjuntos finitos: 1. El dígrafo de una relación reflexiva tiene un lazo en cada vértice. 2. La matriz de la relación tiene aii = 1, es decir que una relación es reflexiva cuando la diagonal de la matriz resultante tiene todos 1. Ejemplo 1 Conjunto Finito Ejemplo Conjunto Infinito Ejemplo 2 Conjunto Finito

Propiedad Simétrica: Una relación R sobre un conjunto X se conoce como simétrica, si (x; y) R se tiene que (y; x) R. Observaciones para conjuntos finitos: 1. El dígrafo de una relación simétrica tiene la propiedad de que si existe un arco dirigido de x a y existe también un arco dirigido de y a x. 2. La matriz de la relación deberá ser simétrica, es decir espejada respecto de la diagonal principal. Ejemplo Conjunto Finito Ejemplo Conjunto Infinito

Propiedad Transitiva: Una relación R sobre un conjunto X se conoce como transitiva si: Dados (x; y) R e (y; z) R se tiene que (x; z) R. Observaciones para conjuntos finitos: 1. El dígrafo de una relación transitiva tiene la propiedad de que siempre que existan arcos dirigidos de “x” a “y” y de “y” a “z” entonces también existe un arco dirigido de “x” a “z”. Ejemplos Conjuntos Finitos Ejemplo Conjunto Infinito

Ejemplo 1 propiedad reflexiva en un conjunto finito: Sea X = { 1, 2, 3, 4 } R = {(1; 1), (1; 2), (1; 3), (1; 4), (2; 2), (2; 3), (2; 4), (3; 3), (3; 4), (4; 4) } La relación R es reflexiva porque para cada elemento x X, se tiene que (x; x) R ; es decir, que (1; 1) R , (2; 2) R , (3; 3) R y (4; 4) R. El dígrafo correspondiente a esta relación es: Continúa ejemplo

Continúa Ejemplo 1 propiedad reflexiva en un conjunto finito: Para verlo en la matriz de la relación: Como todos los elementos de la diagonal principal son 1, la relación es reflexiva.

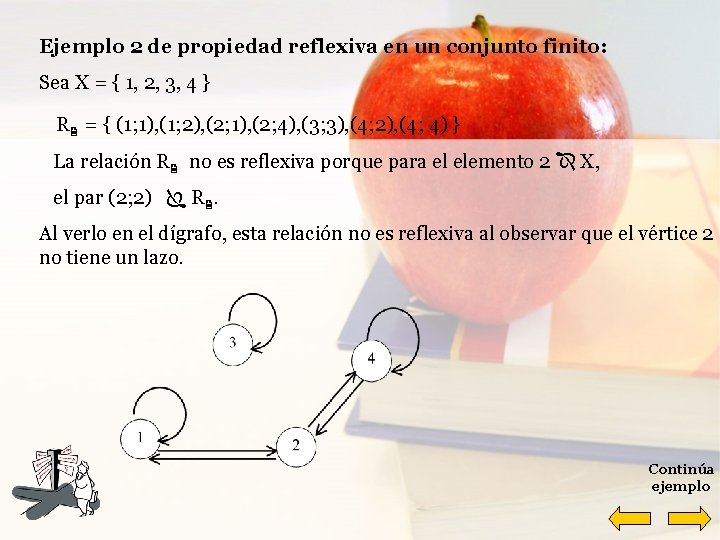
Ejemplo 2 de propiedad reflexiva en un conjunto finito: Sea X = { 1, 2, 3, 4 } R = { (1; 1), (1; 2), (2; 1), (2; 4), (3; 3), (4; 2), (4; 4) } La relación R no es reflexiva porque para el elemento 2 X, el par (2; 2) R. Al verlo en el dígrafo, esta relación no es reflexiva al observar que el vértice 2 no tiene un lazo. Continúa ejemplo

Continúa Ejemplo 2 propiedad reflexiva en un conjunto finito: Para verlo en la matriz de la relación: Claramente se observa que en la diagonal de la matriz de la relación no son todos unos, el elemento a 22 ≠ 1, por lo que la relación no es reflexiva.

Ejemplo propiedad simétrica en un conjunto finito: Sea X = { 1, 2, 3, 4 } R = {(1; 1), (1; 2), (1; 3), (1; 4), (2; 2), (2; 3), (2; 4), (3; 3), (3; 4), (4; 4) } R no es simétrica porque: (1; 2) R y (2; 1) R , (1; 3) R y (3; 1) R , (1; 4) R y (4; 1) R , (2; 3) R y (3; 2) R , (2; 4) R y (4; 2) R , (3; 4) R y (4; 3) R . Nota: Para justificar que R 1 no es simétrica es suficiente uno solo de los casos anteriores. Continúa ejemplo

Continúa Ejemplo propiedad simétrica en un conjunto finito: Mirando el dígrafo de la relación: Se ve que la relación posee la propiedad de que si existe un arco dirigido de x a y no existe también un arco dirigido de y a x, ejemplo es el par (1; 4) donde el (4; 1) no se encuentra en la relación. Otro ejemplo

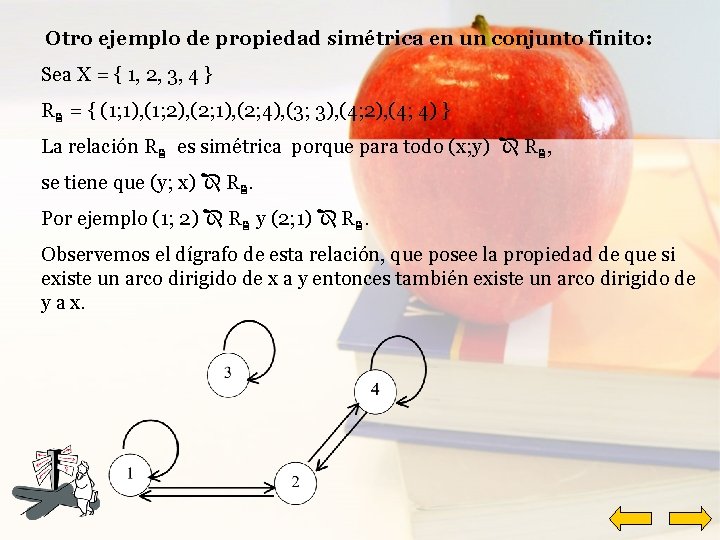
Otro ejemplo de propiedad simétrica en un conjunto finito: Sea X = { 1, 2, 3, 4 } R = { (1; 1), (1; 2), (2; 1), (2; 4), (3; 3), (4; 2), (4; 4) } La relación R es simétrica porque para todo (x; y) R , se tiene que (y; x) R. Por ejemplo (1; 2) R y (2; 1) R. Observemos el dígrafo de esta relación, que posee la propiedad de que si existe un arco dirigido de x a y entonces también existe un arco dirigido de y a x.

Ejemplos de propiedad transitiva en conjuntos finitos: Ejemplo 1: Sea X = { 1, 2, 3, 4 } R = {(1; 1), (1; 2), (1; 3), (1; 4), (2; 2), (2; 3), (2; 4), (3; 3), (3; 4), (4; 4) } Analicemos si siempre: (a; b) R (b; c) R (a; c) R (1; 2) R (2; 3) R y también se cumple el consecuente (1; 3) R Lo mismo ocurre con los pares: (1; 3) y (3; 4) Y también con (2; 3) y (3; 4) Hay casos como (1; 2) R (2; 1) R en los que el condicional (=>) tiene antecedente falso pues (2; 1) R entonces independientemente del valor de verdad del consecuente, la proposición es verdadera. También están los pares del tipo (a; a): (1; 1) R => (1; 1) R Es decir si revisamos todos los casos, siempre es verdadero el condicional, por lo tanto, la relación R es transitiva. Otro ejemplo

Ejemplos de propiedad transitiva en conjuntos finitos: Ejemplo 2: Sea X = { 1, 2, 3, 4 } R = { (1; 1), (1; 2), (2; 1), (2; 4), (3; 3), (4; 2), (4; 4) } La relación R no es transitiva porque por ejemplo: (2; 1) R y (1; 2) R pero (2; 2) R. Al haber encontrado un caso de pares ordenados que hagan verdadero el antecedente y falso el consecuente, es suficiente para afirmar que la relación NO es transitiva.

Veamos un ejemplo de relación de equivalencia en un conjunto infinito: En R (conjunto de los números reales), a. Sb a-b es un número entero. (Tengamos en cuenta que se relacionan aquellos números reales que tengan la misma parte decimal ( mantisa), por ejemplo: 2, 1334 con 36, 1334) Propiedad Reflexiva: a R, se cumple que a-a es un número entero ya que a-a = 0 => a. Sa. Por lo que a. Sa, para todo a R Propiedad Simétrica: Sean a, b R, si a. Sb entonces b. Sa. a. Sb a-b = x, con x Z Si multiplicamos ambos miembros por (-1): -a+b = -x Por propiedad conmutativa: b-a = -x, con –x Z. Por lo que b. Sa, con lo queda probada la propiedad simétrica.

Ejemplo de propiedad reflexiva en un conjunto infinito: En R (conjunto de los números reales), a. Sb a-b es un número entero. (Tengamos en cuenta que se relacionan aquellos números reales que tengan la misma parte decimal ( mantisa), por ejemplo: 2, 1334 con 36, 1334) Propiedad Reflexiva: a R, se cumple que a-a es un número entero ya que a-a = 0 => a. Sa. Por lo que a. Sa, para todo a R, con lo queda probada la propiedad reflexiva.

Ejemplo de propiedad simétrica en un conjunto infinito: En R (conjunto de los números reales), a. Sb a-b es un número entero. (Tengamos en cuenta que se relacionan aquellos números reales que tengan la misma parte decimal ( mantisa), por ejemplo: 2, 1334 con 36, 1334) Propiedad Simétrica: Sean a, b R, si a. Sb entonces b. Sa. a. Sb a-b = x, con x Z Si multiplicamos ambos miembros por (-1): -a+b = -x Por propiedad conmutativa: b-a = -x, con –x Z. Por lo que b. Sa, con lo queda probada la propiedad simétrica.

Ejemplo de propiedad transitiva en un conjunto infinito: En R (conjunto de los números reales), a. Sb a-b es un número entero. (Tengamos en cuenta que se relacionan aquellos números reales que tengan la misma parte decimal ( mantisa), por ejemplo: 2, 1334 con 36, 1334) Propiedad Transitiva: Sean a, b y c R, si a. Sb y b. Sc entonces a. Sc. Si a. Sb entonces a - b= x, con x Z Y si además b. Sc entonces b –c = y, con y Z. Sumando miembro a miembro: (a-b)+(b-c)= x-y. Operando en el primer miembro queda: a-c = x –y que es un número entero por serlo x e y entonces a. Sc, con lo queda probada la propiedad transitiva.

Propiedad Transitiva: Sean a, b y c R, si a. Sb y b. Sc entonces a. Sc. Si a. Sb entonces a - b= x, con x Z Y si además b. Sc entonces b –c = y, con y Z. Sumando miembro a miembro: (a-b)+(b-c)= x-y. Operando en el primer miembro queda: a-c = x –y que es un número entero por serlo x e y entonces a. Sc, con lo queda probada la propiedad transitiva. Por lo tanto, por ser REFLEXIVA, SIMETRICA Y TRANSITIVA, S es una relación de EQUIVALENCIA

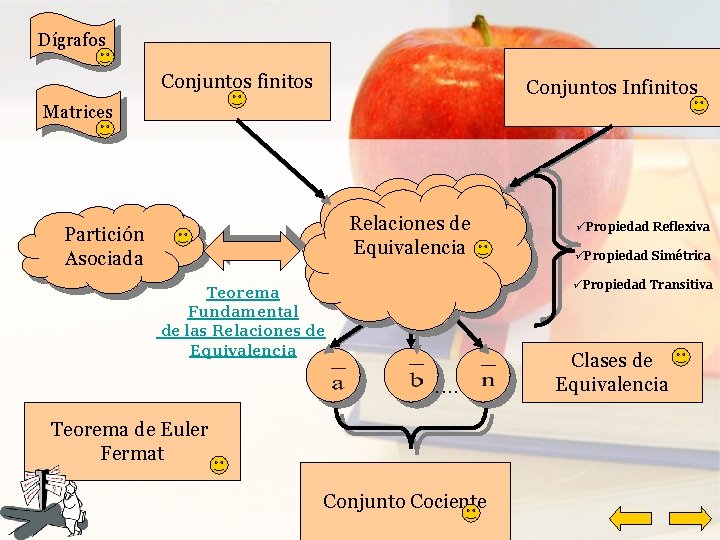
Dígrafos Conjuntos finitos Conjuntos Infinitos Matrices Partición Asociada Teorema Fundamental de las Relaciones de Equivalencia Relaciones de de Equivalencia Equivalenci a. . Teorema de Euler Fermat Conjunto Cociente üPropiedad Reflexiva üPropiedad Simétrica üPropiedad Transitiva Clases de Equivalencia

Relaciones de equivalencia en conjuntos finitos Si el conjunto A es finito, es posible representar la relación mediante: 1. Dígrafos o grafos dirigidos. Sea A un conjunto de aristas, lados o arcos y sea V un conjunto no vacío de elementos llamados vértices o nodos, el grafo es la terna Ejemplo Dígrafo G = (V; A; ) con A V x V 2. Matrices Booleanas: Sean A y B dos conjuntos finitos con |A| = m y |B| = n y sea R: A -> B una relación, llamamos matriz de la relación R o matriz de adyacencia de R a la matriz 1 si (i; j) R 0 si (i; j) R Si A = B Ejemplo Matriz Booleana

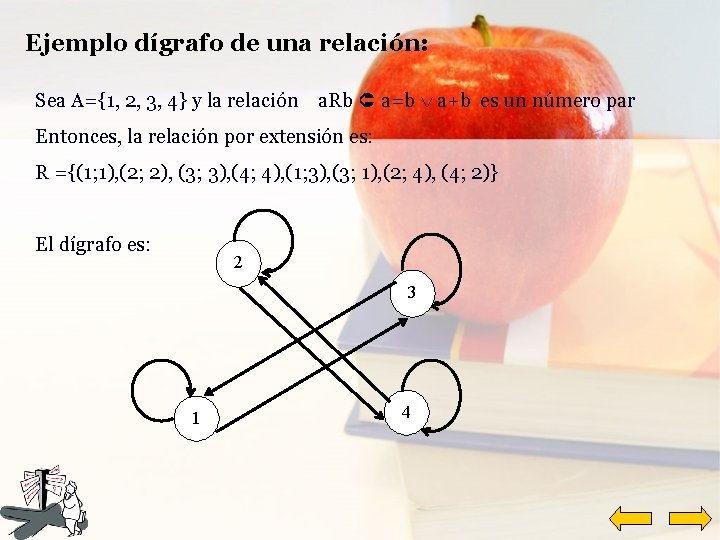
Ejemplo dígrafo de una relación: Sea A={1, 2, 3, 4} y la relación a. Rb a=b a+b es un número par Entonces, la relación por extensión es: R ={(1; 1), (2; 2), (3; 3), (4; 4), (1; 3), (3; 1), (2; 4), (4; 2)} El dígrafo es: 2 3 1 4

Ejemplo de la matriz booleana de la relación: A={1, 2, 3, 4}, a. Rb a=b a+b es un número par, la relación R ={(1; 1), (2; 2), (3; 3), (4; 4), (1; 3), (3; 1), (2; 4), (4; 2)} La matriz es: Para cada elemento se tiene, R (1) = { 1, 3 } = R (3) R (2) = { 2, 4 } = R (4)

Clase de equivalencia: Si R es una relación de equivalencia en A, llamamos Clase de equivalencia de a, al subconjunto de A cuyos elementos son los que se relacionan con a. Lo indicamos [a]={x A / x. Ra}= Tengamos en cuenta que la clase de equivalencia de a es nada más que el conjunto de imágenes que la relación R le asigna al elemento a. Concretando, si R es una relación de equivalencia, R(a)=[a]= . Ejemplos Propiedades de las clases

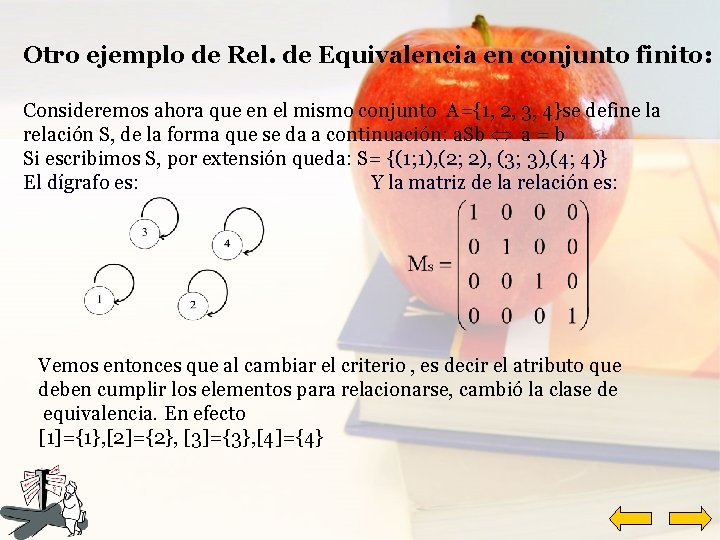
Otro ejemplo de Rel. de Equivalencia en conjunto finito: Consideremos ahora que en el mismo conjunto A={1, 2, 3, 4}se define la relación S, de la forma que se da a continuación: a. Sb a = b Si escribimos S, por extensión queda: S= {(1; 1), (2; 2), (3; 3), (4; 4)} El dígrafo es: Y la matriz de la relación es: Vemos entonces que al cambiar el criterio , es decir el atributo que deben cumplir los elementos para relacionarse, cambió la clase de equivalencia. En efecto [1]={1}, [2]={2}, [3]={3}, [4]={4}

Ejemplos de Clases de Equivalencia 1. Para R, a. Sb a-b es un número entero. La clase de 0 es: [0]= { x R / mant. x = 0}= Z La clase de 2, 3366749308 es: [2, 3366749308]={ x R / mant. x= 3366749308} 2. En Q-{0}, a. Tb a=b a. b=7 [5] ={5, 7/5} [7/5]={7/5, 5} [14]={14, 17/2} Otros ejemplo

Más ejemplos de Clases de Equivalencia 3. Para cada uno de los siguientes casos calcularemos la imagen que la relación le asigna a cada elemento y luego obtendremos las clases: 3. 1. Para A={1, 2, 3, 4, 5, 6} , se define la relación R: A A tal que: a. Rb a=b a+b es un número par. R(1)= {1, 3, 5}= R(3)= R(5)= [1]=[3]=[5] R(2)={2, 4, 6}=R(4)=R(6)=[2]=[4]=[6] 3. 2. Sea R el conjunto de los números reales, se define la relación S: R R tal que: a. Sb a-b es un número entero. a R: R(a)={x R/x-a=z, z Z} = {x R/x=a+z, z Z} = ={x R/ mant (x) = mant. a} = [a] 3. 3. En Q-{0}, a. Tb a=b a. b=7 a Q-{0}: T(a)={x Q-{0}/ x=a x=7/a}=[a]

Algunas propiedades de las clases de equivalencia: Consideremos que R es una relación de equivalencia definida en un conjunto A, Propiedad 1 a A: [a] ≠ ( se verifica porque se cumple la propiedad reflexiva y por lo tanto a R a a [a] ≠ ) Propiedad 2 Si a [b] b [a] ( si a [b] a R b ( por definición de clase de equivalencia) b R a ( por la propiedad simétrica) b [a] (por la definición de clase de equivalencia) y por lo tanto queda probada. Propiedad 3 Para dos clases de equivalencia cualesquiera puede ocurrir que sean iguales o que no tengan ningún elemento en común, es decir: [a]=[b] [a] [b] =. Veamos como probarla:

Si [a]=[b] no hay nada que probar. Nuestro problema se da cuando las clases son distintas y en ese caso debemos mostrar que no tienen elementos en común. Usaremos el contrarrecíproco para llegar a un absurdo (queremos contradecir la hipótesis que, en este caso, significa probar que las clases de equivalencia son iguales), es decir: supondremos que [a] [b] , es decir existe x A tal que x [a] x [b] ( por la definición de intersección) x R a x R b ( por la definición de clase de equivalencia). Consideremos ahora un elemento m [a] a R m, de donde se tiene x R a a R m x R m (por ser x un elemento de la clase de a y propiedad transitiva). Usando la propiedad simétrica queda m R x, como x es un elemento de la clase de b, queda: m R x x R b m R b ( por propiedad transitiva) m [b] [a] [b] De la misma forma se puede probar que [b] [a]. Se usa la definición de igualdad de conjuntos y se probó que las clase de equivalencia son iguales, y ahí está el ABSURDO que provino de suponer que clases de equivalencia distintas tenían elementos en común!!!!!!, por lo tanto queda probada la propiedad 3.

Conjunto Cociente Es el conjunto de las clases de equivalencia que determina la relación R en el conjunto A. Es decir, el conjunto cociente de A, módulo R (que determina R en A) es el conjunto de las clases de equivalencia. Lo indicamos A/R={[a] / a A} Decimos que el conjunto cociente es el conjunto cuyos elementos son subconjuntos de A donde ninguno es vacío, la unión de todos es A y la intersección de dos cualesquiera es el conjunto vacío. Todo ésto ocurre debido a que los elementos del conjunto cociente son clases de equivalencia.

Partición de un conjunto A La partición de un conjunto A es un subconjunto P del conjunto partes de A que cumple las siguientes condiciones 1. X P X ≠ 2. x A X P / x X 3. X, Y P , X ≠ Y X Y = Observemos que las condiciones que le pedimos a un subconjunto P, del conjunto de partes de A, son las mismas que cumple el conjunto Cociente. Veamos: La condición 1. se verifica porque ninguna clase de equivalencia es vacía. La condición 2. se verifica porque para cada elemento existe su clase de equivalencia. La condición 3. se verifica pues dos clases de equivalencia son iguales o no tienen ningún elemento en común.

Teorema fundamental de las relaciones de equivalencia Toda relación de equivalencia definida en un conjunto determina en él una partición (conjunto cociente). Recíprocamente, toda partición de un conjunto induce en él una relación de equivalencia. Es decir hay tantas relaciones de equivalencia como particiones posibles en un conjunto A.

Ejemplo del Teorema Fundamental de las Relaciones de Equivalencia. ¿ Cuántas relaciones de equivalencia hay en A={1, 2, 3}? La respuesta es 5, R ={(1; 1), (2; 2), (3; 3)}, R 2= {(1; 1), (2; 2), (3; 3), (1; 2), (2; 1)}, R 3={(1; 1), (2; 2), (3; 3), (1; 3), (3; 1)}, R 4={(1; 1), (2; 2), (3; 3), (2; 3), (3; 2)} R 5= A A

Congruencias Congruencia Módulo n: En el conjunto de los enteros se define la relación: a R b a b (n) n a - b Se lee “a es congruente con b módulo n” Probaremos que esa relación es de equivalencia Reflexiva: x Z : x - x = 0 n n x - x x x (n) Simétrica: x, y Z : x R y x y (n) n x - y = n k k Z - ( x - y) = - n k y - x = n (-k) -k Z n y - x y x (n) y R x Transitiva: x , y , z Z : x R y y R z x y (n) y z (n) n x - y n y - z x - y = n k k Z y - z = n t t Z sumando miembro a miembro x - y + y - z = n k + n t x - z = n (k + t) k+t Z n x - z x z (n) x R z

(sigue Congruencias) Veamos que pasa si n=3 (Congruencia módulo 3) Las clases de equivalencia son: • cl(0) = { x Z / x = 3 k con k Z } O sea que en la clase del cero están todos los múltiplos de 3. • cl(1) = = { x Z / x = 3 k + 1 con k Z } O sea que en la clase del uno están todos los enteros que al dividir por 3 dan resto 1. • cl(2) = = { x Z / x = 3 k + 2 con k Z } O sea que en la clase del dos están todos los enteros que al dividir por 3 dan resto 2.

(sigue Congruencias) ¿Nos quedó algún entero sin saber en qué clase está? NO. Por lo tanto, podemos escribir el conjunto cociente: Z/R = { cl(0), cl(1), cl(2) } Es decir, que solamente hay 3 clases pero con infinitos elementos dentro de cada una. Nota: en vez de escribir el conjunto cociente Z/R se escribe Z 3 A las clases de equivalencia de esta relación se les suele decir clases residuales, ya que son los restos de dividir por 3.

(sigue Congruencias) ¿Cómo será Z 4 , Z 5 y en general Zn ? Z 4 = { cl(0), cl(1), cl(2), cl(3) } Z 5 = { cl(0), cl(1), cl(2), cl(3), cl(4) } Zn = { cl(0), cl(1), , cl(n-1) } Pero, cuidado!!! , por ejemplo, la cl(2) en la congruencia módulo 5 NO es la misma cl(2) en la congruencia módulo 4.

Algunas otras cuestiones sobre congruencias q La relación R es la “congruencia módulo n” y como toda relación de equivalencia clasifica a los números enteros según un atributo, en este caso es su resto en la división por n (determina n restos {0, 1, …. . , (n-1)}). q El conjunto cociente constituye un sistema completo de restos módulo n. Por ejemplo, si n= 5, el sistema completo de restos módulo 5 es {0, 1, 2, 3, 4}. q Algo para tener en cuenta es que un conjunto de números enteros que producen un sistema completo de restos módulo n, se dice que constituyen un sistema completo de enteros incongruentes módulo n. Veamos el siguiente caso: el conjunto {10, 21, 32, 63, 84} son un sistema incongruente módulo 5 porque al dividirlos por 5 el resto es, respectivamente {0, 1, 2, 3, 4}, es decir todos restos distintos.

q Si el conjunto de enteros que se elige son enteros primos con n se obtiene un sistema reducido de restos módulo n. (son los números enteros positivos, es decir naturales, que son menores o iguales a n y además son coprimos con n). Es decir que la totalidad de restos r tales que 1 r n, coprimos con n, forma un sistema reducido de restos módulo n. Cualquier otro sistema tiene el mismo número de elementos, ese número se indicará (n) y se conoce como función de Euler. Formalmente, (n) = { x N / x n (x, n) = 1}

Ejemplos de función de Euler: Para aclarar ideas veamos algunos casos: q (1)=1 q (2) = 1 q (3)={ x N / x 3 (x, 3)=1}={1, 2}=2 q (4)={ x N / x 4 (x, 4)=1}={1, 3}=2 q (15)={ x N / x 15 (x, 15)=1}= ={1, 2, 4, 7, 8, 11, 13, 14}=8 q (12)={ x N / x 12 (x, 12)=1}= ={1, 5, 7, 11}=4

Propiedades de función de Euler: 1. Si p es un número primo, (p)= p-1, Por ejemplo 2, 3, son primos y en ambos casos se verifica la propiedad ya que (2)=1 y (3)=2 2. Si n es un número natural cualquiera y p es un número primo se tiene: φ(pn) = pn(1 -1/p) Que puede escribirse: φ(pn) = pn-1(p-1) Por ejemplo para p =7, n = 3, se tiene: φ(73) = 72(7 -1) = 72. 6

Otra propiedad de la función de Euler: 3. Si n, m son números naturales y (n, m) = 1 se tiene que (n. m)= (n). (m) Ejemplo: Para si n=5, m=4, resulta (4. 5)= (4). (5)= 2. 4 = 8 Tengamos en cuenta que se calculó (4) y que como 5 es primo, (5)= 5 -1 = 4 Recordemos que si n es un número entero distinto de 0, 1, -1 , se puede probar que: ( Teorema fundamental de la aritmética) A partir de ahí se tiene,

Ejemplo para aplicar la propiedad anterior: Calculemos ¿Qué significa esto? , significa que los números coprimos con 48 que no son divisibles ni por 2 ni por 3 son 16, veamos cuales: {1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37, 41, 43, 47}, por lo tanto hemos verificado la propiedad.

Ecuación lineal de congruencia Una expresión de la forma: a. x b(n) se denomina ecuación lineal de congruencia. Muchas veces esa ecuación no tiene solución, en efecto alcanza con observar el caso que se da a continuación: 2 x 3(2), la primera de las cosas que hay que tener en cuenta es que la solución se debe encontrar en Z 2, eso nos indica que los valores posibles son 0, 1 Si x= 0 , debe ser 0 3(2) cosa que no es posible ya que 2 no es divisor de -3 Si x = 1, debería pasar que 2 3(2) lo cual significa que 2 divide a (-1) lo cual tampoco es verdadero.

Otro ejemplo de ecuación lineal de congruencia Veamos ahora la siguiente ecuación : 3 x 7 (11), la debemos resolver en Z 11={ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} Operando queda que x = 6 es la solución , pero también se tiene que, x = 6 + k. 11 es solución que podemos verificar reemplazando en la ecuación y ver que se satisface la igualdad: 3 ( 6 + k 11) 7 (11) ya que 11 | 3 (6+ k 11)-7, En efecto: 3(6+ k 11)-7 = 18+33 k-7 = 11+33 k =11(1+3 k)

En general si x es una solución entonces x+ k. n también es una solución. Como son infinitas las soluciones consideraremos, 0 x n y las llamaremos soluciones principales. En nuestro caso x = 6 es la única solución principal. Veamos ahora condiciones suficientes, necesarias y necesaria y suficiente para que ecuación lineal de congruencia tenga solución.

Condición suficiente para que una ecuación de congruencia tenga solución Si en a. x b(n) el máximo común divisor entre a y n, que indicamos (a, n) = 1 entonces hay solución. Esta condición no es necesaria, como se ve en el caso siguiente: 2 x 2(4) , las soluciones estarán en Z 4= { 0, 1, 2, 3} Si x=1 ó x = 3 hay solución !!!!!! y sin embargo (a, n) = ( 2, 4)= 2 1

La condición necesaria y suficiente para que la ecuación a. x b (n) admita una solución es que (a, n) b La solución es: Veamos el siguiente ejemplo: 5. x 14 (8), como (5, 8) = 1 hay solución en Z 8 (8) = 8. (1 -1/2)= 4 Reemplazando se tiene: x=54 -1. 14 =53. 14= 125. 14 14 6(8) y 125 - 64 = 61, y 61 5(8) resulta que la solución: x=5. 6(8) = 6

Aplicación de la congruencia Es importante la utilización de congruencias para asignar localizaciones de memorias de una computadora a los datos o registros de un fichero. Supongamos una base de datos de los alumnos de primer año de UTN-FRBA que cursan Matemática Discreta y veamos un procedimiento rápido para recuperar algunos de los datos: En primer lugar el registro correspondiente a cada alumno tiene una clave, que puede ser, por ejemplo el número de su documento o su legajo.

(Continúa Aplicación de la congruencia) Hay, por lo tanto una función que asigna la localización de memoria f(k) al registro cuya clave es k. Este tipo de asignación se conoce con el nombre de función hash. Una de las más comunes es la siguiente: f(k)= k (mod n), donde n es el número de posiciones de memoria disponibles. Es decir que, si tuviéramos 1270 lugares de memoria y el número de documento de un alumno fuera 47254313: f(47254313)=47254313 mod 1270= 81 De esta forma podría ocurrir que a dos estudiantes les correspondiera la misma localización de memoria.

(Continúa Aplicación de la congruencia) Este hecho se conoce con el nombre de colisión. Para evitarla se podría , por ejemplo , asignar a uno de esos alumnos la primera posición vacante en la memoria.

Enunciaremos ahora un teorema que es de uso para resolver cuestiones relativas a la seguridad informática: Teorema de Euler Fermat Si (a, n)=1 a φ(n) 1 (n) Teorema de Euler-Fermat Si p es primo a p a (p) Teorema de Fermat Otra versión es: a p-1 1 (p)

Ejemplo de aplicación Calcular el resto en la división de 7122 por 11 Solución: Como 122= 10. 12 +2 , se tiene que: 7 122 = 7 10. 12 + 2 = 7 10. 12 7 2 = 7 (11 -1)12 7 2 = [7(11 -1)]12 72 Teniendo en cuenta que ap-1 1 (p) resulta [711 -1]12 1 (11) Entonces: 7 122 72 (11) De donde el resto de dividir 7 122 por 11 es el mismo que dividir 49 por 11, o sea 5.

Ejercicios Complejidad Baja Complejidad Media Complejidad Alta

Complejidad Baja 1. En A={1, 2, 3, 4, 5} se define la relación R, por enumeración: R={(1; 1), (2; 2), (3; 3), (4; 4), (5; 5), (1; 4), (4; 1), (2; 5), (5; 2), (5; 1), (1; 5), (1; 2), (2; 1)} Halle el dígrafo asociado a la relación y la matriz. 2. ¿Cuáles de las siguientes relaciones son de equivalencia? a. b. c. d. A={1, 2, 3, 4, 5, 6} , a. Rb a=b a+b es un número par. En R, a. Sb a-b es un número entero En R, a. Tb a b A={1, 2, 3, 4, 5, 6}, a. Rb (a, b)=1 Mas ejercicios

Complejidad Baja 3. En el conjunto A= { 1, 2, 3, 4, 5 } se define la relación R tal que: x R y x+y = 6 a). Halle la matriz de la relación (R compuesta con R) y luego la matriz de S = R b). Analice si S es de equivalencia, en caso afirmativo halle las clases y el conjunto cociente. Si no lo es, justifique propiedad no cumple. 4. Determine si las siguientes relaciones son de equivalencia. a). En Q-{0}, a. Tb a=b a. b=7 b). En A={1, 2, 3, 4, 5, 6}, a. Pb a-b= 2. k, k entero Mas ejercicios

Complejidad Baja 5. Sea el conjunto A = { 1, 2, 3, 4, 5, 6 }. Haga el dígrafo y escriba la matriz de una relación R sabiendo que es de equivalencia, hay 3 clases de equivalencia, 5 cl(6), y en total hay 14 pares ordenados en R. 6. Analice si en el conjunto B = {1, 2, 3, 4, 5, 6, 7} es posible definir una relación de equivalencia que esté formada exactamente por 19 pares ordenados y tales que cl(1) cl(2) cl(3) (las clases de 1, 2 y 3 sean todas distintas dos a dos). En caso afirmativo indicarla. Mas ejercicios

Complejidad Baja 7. Calcule los siguientes restos: Ø 5417 por 3 Ø 47 7385 por 17 Ø 1815230 por 7 Ø 31037 por 61 Ø 31037 por 17 Ø 712 por 11 Ø 123456 por 31 Ø 31000 por 7

Complejidad Media 1. En R ( conjunto de los números reales) se define la relación de equivalencia: x R y x 2 - 8 = y 2 – 8| a) Grafique la relación. b) Halle las clases de equivalencia y el conjunto cociente. 2. Dada la relación S definida en |R+ tal que: x S y log(x) = log(y) , a) Demuestre que S es de equivalencia. b) Halle las clases de equivalencia del 1, del 2, del 5 y la genérica clase de x. c) Escriba el conjunto cociente correspondiente a la relación S. Mas ejercicios

Complejidad Media 3. Sea A= {1, 2, 3, 4}, en P(A ) se define la siguiente relación: X R Y X B = Y B con B = { 2, 4} a) Probar que R es de equivalencia. b) Hallar las clases de equivalencia. c) Hallar el conjunto cociente. 4. Analizar la validez de las siguientes afirmaciones: Ø Ø Ø Ø Ø 11 -1(6) 13 0(2) 102 10( 3) 270 15 (54) 31 -18(7) 3 3(2) n 0 (n) 1 -1(2) 90 -1 (13) Mas ejercicios

Complejidad Media 5. Analizar la validez de las siguientes proposiciones :

Complejidad Alta 1. Indicar los valores de n que hacen verdaderas las congruencias siguientes: Ø Ø Ø Ø 5 4(n) 5 -4(n) 1197 186(n) 1214567 3124567 (10 n) 1 0 (n) 3 -3 (n) 1197 -286 (n) Mas ejercicios

Complejidad Alta 2. En |R 2 se define la relación de equivalencia: (x; y) S (a; b) x - 3 = a - 3 a) Demuestre que S es de equivalencia. b) Halle las clases de equivalencia y el conjunto cociente. 3. Sea la relación de equivalencia: f R g Im(f) = Im(g) definida en el conjunto de funciones con dominio y codominio en |R. Halle tres elementos de la clase de f(x) = x 2 - 4. Mas ejercicios

Complejidad Alta 4. Demuestre que la intersección de dos relaciones de equivalencia es también una relación de equivalencia. Analice si ocurre lo mismo con la unión. 5. Sea R la relación en el conjunto de todas las personas que han visitado una página web determinada, tal que x. Ry la persona x y la persona y, han seguido el mismo conjunto de enlaces a partir de esta página web (yendo de una página web a otra hasta que se desconectan de Internet). Demostrar que R es una relación de equivalencia. Mas ejercicios

Complejidad Alta 6. a) Demostrar que la relación S, que consiste en todos los pares (x; y) en los que x e y son cadenas de bits de longitud al menos tres que coinciden en sus tres primeros bits, es una relación de equivalencia en el conjunto de todas las cadenas de bits de longitud al menos tres. b) ¿Cuáles son las clases de equivalencia de estas cadenas de bits para la relación S? 010; 1011; 11111; 010101. 7. Definir una relación de equivalencia en el conjunto de estudiantes de tu curso de matemática discreta. Determinar las clases de equivalencia para esa relación. Mas ejercicios

Complejidad Alta 8. Demostrar, justificando , cada una de las siguientes propiedades: Mas ejercicios

Complejidad Alta 9. Resolver los siguientes casos: Ø 2 x 7(7) Ø 3 x 7(11) Ø 10 x 9(3) Ø 518 x 72(13) Ø 23 x 41(52) Ø 42 x 50(76) Ø 30 x 18(78) Ø 27 x 6(3) Ø 102 x 14(12) Ø 35 x 14(182¡)

Complejidad Baja - Respuestas 1. En A={1, 2, 3, 4, 5} se define la relación R, por enumeración: R={(1; 1), (2; 2), (3; 3), (4; 4), (5; 5), (1; 4), (4; 1), (2; 5), (5; 2), (5; 1), (1; 5), (1; 2), (2; 1)} El dígrafo es: 2 3 5 1 4

Complejidad Baja - Respuestas La matriz booleana es: MR = Es una relación de equivalencia ya que en la matriz hay solamente unos en la diagonal principal ( se cumple la reflexividad), la relación es simétrica ya que, por ejemplo, la matriz MR = (MR)t , se cumple la propiedad, y además es transitiva pues (MR)2 ≤ MR.

Complejidad Baja - Respuestas 2. ¿Cuáles de las siguientes relaciones son de equivalencia? a. A={1, 2, 3, 4, 5, 6} , a. Rb a=b a+b es un número par. R es relación de equivalencia b. En R, a. Sb a-b es un número entero S es relación de equivalencia c. En R, a. Tb a b No es relación de equivalencia d. A={1, 2, 3, 4, 5, 6}, a. Rb (a, b)=1 No es relación de equivalencia

Complejidad Baja - Respuestas 3. En el conjunto A= { 1, 2, 3, 4, 5 } se define la relación R tal que: x R y x+y = 6 a) Halle la matriz de la relación R 2 (R compuesta con R) y luego la matriz de S = R U R 2. Matriz de R (ordenados los elementos de menor a mayor): M(R) = M(S) = M(R) M(R 2) = M(R) =

Complejidad Baja - Respuestas b) Analice si S es de equivalencia, en caso afirmativo halle las clases y el conjunto cociente. Si no lo es, justifique propiedad no cumple. S es de equivalencia ya que: 1. S es reflexiva (la diagonal de la matriz de S tiene todos los elementos 1) 2. S es simétrica (la matriz de S es igual a su traspuesta) 3. S es transitiva (la matriz de S 2 es menor o igual que la matriz de S) M(S 2) = M(S) = = El conjunto cociente es: A/S = { {1, 5} , {2, 4}, {3} }

Complejidad Baja - Respuestas 4. Determine si las siguientes relaciones son de equivalencia. a). En Q-{0}, a. Tb a=b a. b=7 Sí, es relación de equivalencia b). En A={1, 2, 3, 4, 5, 6}, a. Pb a-b= 2. k, k entero Sí, es relación de equivalencia

Complejidad Baja - Respuestas 5. Sea el conjunto A = { 1, 2, 3, 4, 5, 6 }. Haga el dígrafo y escriba la matriz de una relación R sabiendo que es de equivalencia, hay 3 clases de equivalencia, 5 cl(6), y en total hay 14 pares ordenados en R. Como debe haber 3 clases de equivalencia y el conjunto tiene 6 elementos, podrían darse los siguientes casos: caso 1: 3 clases de 2 elementos cada una caso 2: 1 clase de 4 elementos, y 2 clases unitarias caso 3: 1 clase de 3 elementos, 1 clase de 2, y 1 clase unitaria Veamos la cantidad de pares ordenados en cada uno de los casos: caso 1: en cada clase hay 4 pares, o sea en total 12. No es lo pedido. caso 2: la clase de 4 elementos tiene 16 pares, ya nos pasamos. caso 3: la clase de 3 elementos tiene 9 pares, la de dos elementos tiene 4 y la unitaria uno solo. En total son 9 + 4 + 1 = 14. Esta sí nos sirve.

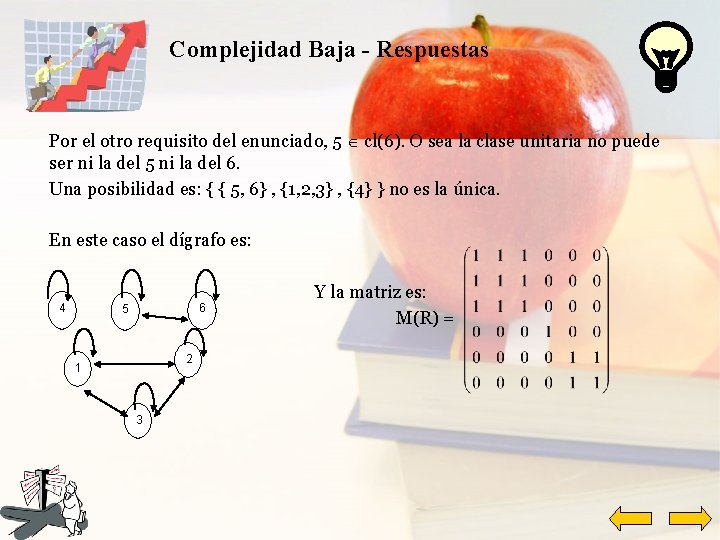
Complejidad Baja - Respuestas Por el otro requisito del enunciado, 5 cl(6). O sea la clase unitaria no puede ser ni la del 5 ni la del 6. Una posibilidad es: { { 5, 6} , {1, 2, 3} , {4} } no es la única. En este caso el dígrafo es: Y la matriz es: 4 6 5 M(R) = 2 1 3

Complejidad Baja - Respuestas 6. Analice si en el conjunto B = {1, 2, 3, 4, 5, 6, 7} es posible definir una relación de equivalencia que esté formada exactamente por 19 pares ordenados y tales que cl(1) cl(2) cl(3) (las clases de 1, 2 y 3 sean todas distintas dos a dos). En caso afirmativo indicarla. Para que haya 19 pares puede haber 2 celdas de 3 elementos y una celda unitaria. Por ejemplo: cl(1) = { 1, 4, 5 } cl(2) = { 2 , 6, 7 } cl(3) = { 3 }

Complejidad Media - Respuestas 1. En |R se define la relación de equivalencia: x R y x 2 - 8 = y 2 – 8| a) Grafique la relación. x R y x 2 - 8 = y 2 - 8 x 2 - 8 = y 2 – 8 x 2 - 8 = - y 2 + 8 x 2 = y 2 x 2 + y 2 = 16 y = x y = -x x 2 + y 2 = 16 ( Son 2 rectas y una circunferencia) 4 -4

Complejidad Media - Respuestas b) Halle las clases de equivalencia y el conjunto cociente. Por lo desarrollado anteriormente y teniendo en cuenta la definición de clase de equivalencia: cl(x) = { y R / y = x y = -x x 2 + y 2 = 16 } Por ejemplo: cl(1) = { 1 , -1 , √ 15 , -√ 15} cl(2) = { 2 , -2 , √ 12, -√ 12} cl(√ 8) = {√ 8, -√ 8} pues en x =√ 8 se cruzan las rectas con la circunferencia cl(4) = { 4 , -4 , 0 } cl(5) = { 5 , -5 } Elijo tomar como representante de cada clase al elemento mayor, por lo tanto el conjunto de índices es: I = √ 8, + ) Si x =√ 8 cl(√ 8) = {√ 8, -√ 8} Si x √ 8, 4) cl(x) = { x , - x , √(16 -x 2), -√(16 -x 2) } Si x = 4 cl(4) = { 4 , -4 , 0 } Si x (4 , + ) cl(x) = { x , - x } Y el conjunto cociente queda: R / R = { cl(x) / x √ 8, + ) }

Complejidad Media - Respuestas 2. Dada la relación S definida en |R+ tal que: x S y log(x) = log(y) , a) Demuestre que S es de equivalencia 1). x |R+ : log(x) = log(x) x S x, S es reflexiva 2). x, y |R+ : x S y log(x) = log(y) = log(x) y S x, S es simétrica 3). x, y, z |R+ : x S y y S z log(x) = log(y) = log(z) log(x) = log(z) x S z, S es transitiva Por cumplir las tres propiedades demostradas, S es de equivalencia.

Complejidad Media - Respuestas b) Halle las clases de equivalencia del 1, del 2, del 5 y la genérica clase de x. cl(x) = { y |R+ / log(y) = log(x) } = { y |R+ / log(y)= log(x) log(y) = -log(x) } = { y |R+ / y = x y = 1/x } Entonces las clases pedidas son: cl(1) = { 1 } cl(2) = { 2, ½ } cl(5) = { 5, 1/5 } c) Escriba el conjunto cociente correspondiente a la relación S. |R+ / S = { cl(x) / x 1; + ) }

Complejidad Media - Respuestas 3. Sea A= {1, 2, 3, 4}, en P(A ) se define la siguiente relación: X R Y X B = Y B con B = { 2, 4} a) Probar que R es de equivalencia. Probemos que R es reflexiva: X P(A) : X B = X B X R X Probemos que R es simétrica: X, Y P(A) : X R Y X B = Y B = X B Y R X Y ahora transitiva: X, Y, Z P(A) : X R Y Y R Z X B = Y B = Z B X B = Z B X R Z Por lo tanto R es de equivalencia.

Complejidad Media - Respuestas b) Hallar las clases de equivalencia. P(A) = { , {1} , {2} , {3} , {4} , {1, 2} , {1, 3} , {1, 4} , {2, 3} , {2, 4} , {3, 4} , {1, 2, 3} , {1, 2, 4} , {1, 3, 4} , {2, 3, 4} , {1, 2, 3, 4} } Cl( ) = { X P(A) / X {2, 4} = { , {1} , {3} , {1, 3} } Cl( {2} ) = { X P(A) / X {2, 4} = {2} } = { {2} , {1, 2} , {3, 2} , {1, 2, 3} } Cl( {4} ) = { X P(A) / X {2, 4} = {4} } = { {4} , {1, 4} , {3, 4} , {1, 3, 4} } Cl( {2, 4} ) = { X P(A) / X {2, 4} = {2, 4} } = { {2, 4} , {1, 2, 4} , {2, 3, 4} , {1, 2, 3, 4} } c) Hallar el conjunto cociente. Escribamos el conjunto cociente, está formado por todas las clases de equivalencia: P(A) / R = { Cl( ) , Cl( {2} , Cl( {4} ) , Cl( {2, 4} ) }

Complejidad Alta - Respuestas 2. En |R 2 se define la relación de equivalencia: (x; y) S (a; b) x - 3 = a - 3 Demuestre que S es de equivalencia. Debemos probar las tres propiedades: Reflexiva: (x; y) |R 2 : x - 3 = x - 3 (x; y) Simétrica: (x; y) , (z; t) |R 2 : (x; y) S (z; t) x - 3 = z - 3 = x - 3 (z; t) S (x; y) Transitiva: (x; y) , (z; t) , (u; v) |R 2 : (x; y) S (z; t) S (u; v) x - 3 = z - 3 = u - 3 x - 3 = u - 3 (x; y) S (u; v)

Complejidad Alta - Respuestas Halle las clases de equivalencia y el conjunto cociente. cl(x; y) = { (a; b) / x - 3 = a - 3 } = { (a; b) / x - 3 = a - 3 x - 3 = - a + 3 } = { (a; b) / x = a a = - x + 6 } Por ejemplo: cl(1; 2) = { (1; b) , (5; b) / b R} cl(2; 8) = { (2; b) , (4; b) / b R} cl(3; -4) = { (3; b) / b R} Se elije tomar como representante de cada clase al par: (x; 0) con x 3 El conjunto cociente queda: R 2 / S = { cl(x; 0) / x 3 } siendo cl(x; 0) = { (x; b) , (6 -x; b) / b R}

Complejidad Alta - Respuestas 3. Sea la relación de equivalencia: f R g Im(f) = Im(g) definida en el conjunto de funciones con dominio y codominio en |R. Halle tres elementos de la clase de: f(x) = x 2 - 4. Para hallar elementos de la clase de esta función, debemos calcular su imagen: Es una parábola cóncava hacia arriba con vértice en (0, -4) por lo tanto su imagen es: Im(f) = -4, + ) Otras funciones que tengan la misma imagen pueden ser por ejemplo: g(x) = x - 4 h(x) = (x-5)2 - 4

Complejidad Alta - Respuestas 4. Demuestre que la intersección de dos relaciones de equivalencia es también una relación de equivalencia. Analice si ocurre lo mismo con la unión. Hipótesis: R: A A y S: A A son de equivalencia. Tesis: T = R S es de equivalencia Demostración: 1. Probemos que T es reflexiva: x A : (x; x) R (x; x) S por ser ambas reflexivas (hipótesis) (x; x) R S por definición de intersección (x; x) T T es reflexiva 2. Probemos que T es simétrica: x, y A : (x; y) T (x; y) R S (x; y) R (x; y) S por definición de intersección (y; x) R (y; x) S por ser ambas simétricas (hipótesis) (y; x) R S por definición de intersección (y, x) T T es simétrica

Complejidad Alta - Respuestas 3. Probemos que T es transitiva: x, y, z A: (x; y) T (y; z) T (x; y) R S (y; z) R S [ (x; y) R (x; y) S ] [ (y; z) R (y; z) S ] por definición de intersección [ (x; y) R (y; z) R ] [ (x; y) S (y; z) S ] por conmutatividad y asociatividad de la (x; z) R (x; z) S por ser ambas transitivas (hipótesis) (x; z) R S por definición de intersección (x; z) T T es transitiva En cambio, si R y S son de equivalencia, la unión R U S no necesariamente lo es. Mostraremos un contraejemplo: Sea el conjunto A = { 1, 2, 3 } y las relaciones: R = { (1; 2) , (1; 1), (2; 2) , (3; 3) } S = { (1; 3) , (1; 1), (3; 1), (2; 2) , (3; 3) } Ambas son de equivalencia pero su unión: R U S = { (1; 2) , (1; 1), (2; 2) , (3; 3) , (1; 3) , (3; 1) } No es de equivalencia, ya que no es transitiva: (2; 1) RUS (1; 3) RUS pero (2; 3) RUS.