Reinforcement Learning Presentation Markov Games as a Framework

Reinforcement Learning Presentation Markov Games as a Framework for Multi-agent Reinforcement Learning Mike L. Littman Jinzhong Niu March 30, 2004

Overview MDP is capable of describing only single-agent environments. New mathematical framework is needed to support multi-agent reinforcement learning. Markov Games A single step in this direction is explored. 2 -player zero-sum Markov Games as a Framework for Multi-agent Reinforcement Learning 2

Definitions Markov Decision Process (MDP) Markov Games as a Framework for Multi-agent Reinforcement Learning 3

Definitions (cont. ) Markov Game (MG) Markov Games as a Framework for Multi-agent Reinforcement Learning 4

Definitions (cont. ) Two-player zero-sum Markov Game (2 P-MG) Markov Games as a Framework for Multi-agent Reinforcement Learning 5

2 P-MG Is Capable? Yes Precludes cooperation! Generalizes MDPs (when |O|=1) The opponent has a constant behavior, which may be viewed as part of the environment. Matrix Games (when |S|=1) The environment doesn’t hold any information and rewards are totally decided by the actions. Markov Games as a Framework for Multi-agent Reinforcement Learning 6

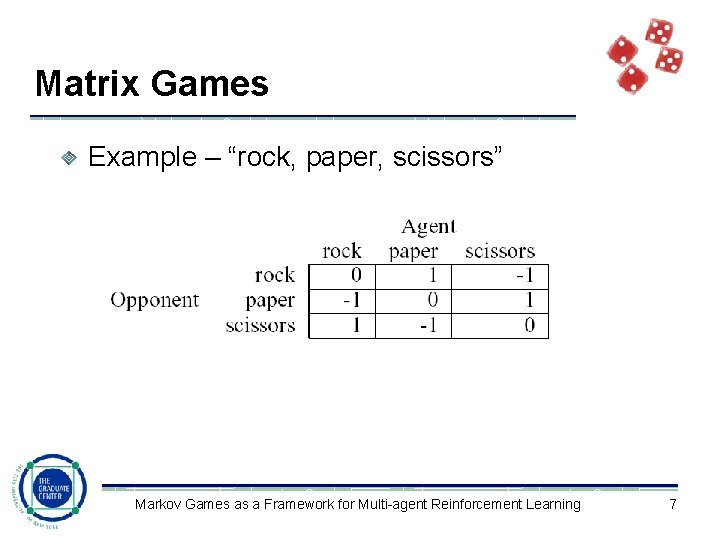
Matrix Games Example – “rock, paper, scissors” Markov Games as a Framework for Multi-agent Reinforcement Learning 7

What does ‘optimality’ exactly mean? MDP A stationary, deterministic, and undominated optimal policy always exists. MG The performance of a policy depends on the opponent’s policy, so we cannot evaluate them without context. New definition of ‘optimality’ in game theory Performs best at its worst case compared with others At least one optimal policy exists, which may or may not be deterministic because the agent is uncertain of its opponent’s move. Markov Games as a Framework for Multi-agent Reinforcement Learning 8

Finding Optimal Policy Matrix Games The optimal agent’s minimum expected reward should be as large as possible. Use V to express the minimum value, then consider how to maximize it Markov Games as a Framework for Multi-agent Reinforcement Learning 9

Finding Optimal Policy - MDP Value of a state Quality of a state-action pair Markov Games as a Framework for Multi-agent Reinforcement Learning 10

Finding Optimal Policy – 2 P-MG Value of a state Quality of a s-a-o triple Markov Games as a Framework for Multi-agent Reinforcement Learning 11

Learning Optimal Polices Q-learning minimax-Q learning Markov Games as a Framework for Multi-agent Reinforcement Learning 12

Minimax-Q Algorithm Markov Games as a Framework for Multi-agent Reinforcement Learning 13

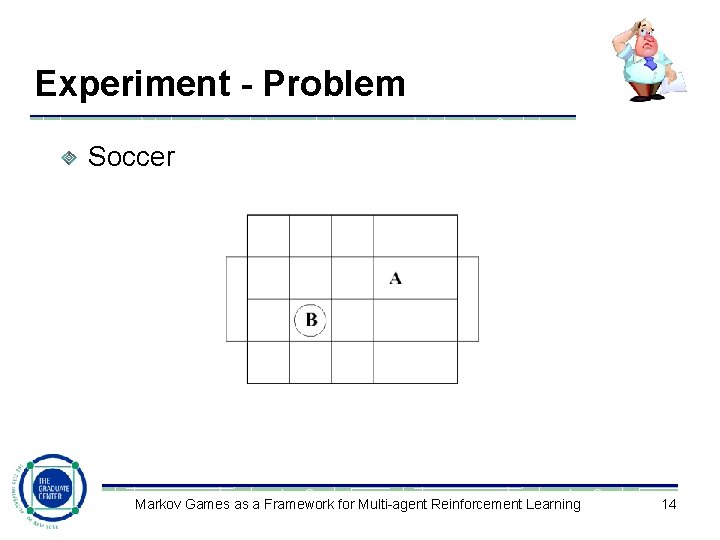
Experiment - Problem Soccer Markov Games as a Framework for Multi-agent Reinforcement Learning 14

Experiment - Training 4 agents trained through 106 steps minimax-Q learning vs. random opponent - MR vs. itself - MM Q-learning vs. random opponent - QR vs. itself - QQ Markov Games as a Framework for Multi-agent Reinforcement Learning 15

Experiment - Testing Test 1 QR > MR? Test 3 QR, QQ – 100% loser? Test 2 QR<<QQ? Markov Games as a Framework for Multi-agent Reinforcement Learning 16

Contributions A solution to 2 -player Markov games with a modified Q-learning method in which minimax is in place of max Minimax can also be used in single-agent environments to avoid risky behavior. Markov Games as a Framework for Multi-agent Reinforcement Learning 17

Future work Possible performance improvement of the minimax-Q learning method Linear programming caused large computational complexity. Iterative methods may be used to get approximate solutions to minimax much faster, which is sufficiently satisfactory. Markov Games as a Framework for Multi-agent Reinforcement Learning 18