Reinforcement Learning Mitchell Ch 13 see also Barto

Reinforcement Learning Mitchell, Ch. 13 (see also Barto & Sutton book on-line)

Rationale • Learning from experience • Adaptive control • Examples not explicitly labeled, delayed feedback • Problem of credit assignment – which action(s) led to payoff? • tradeoff short-term thinking (immediate reward) for long-term consequences

Agent Model • Transition function – T: Sx. A->S, environment • Reward function R: Sx. A->real, payoff • Stochastic but Markov = • Policy=decision function, p: S->A • “rationality” – maximize long term expected reward – Discounted long-term reward (convergent series) – Alternatives: finite time horizon, uniform weights
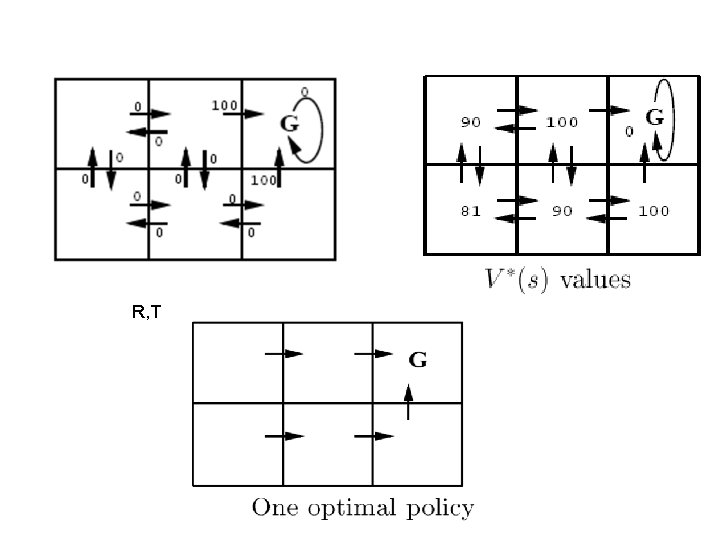
R, T
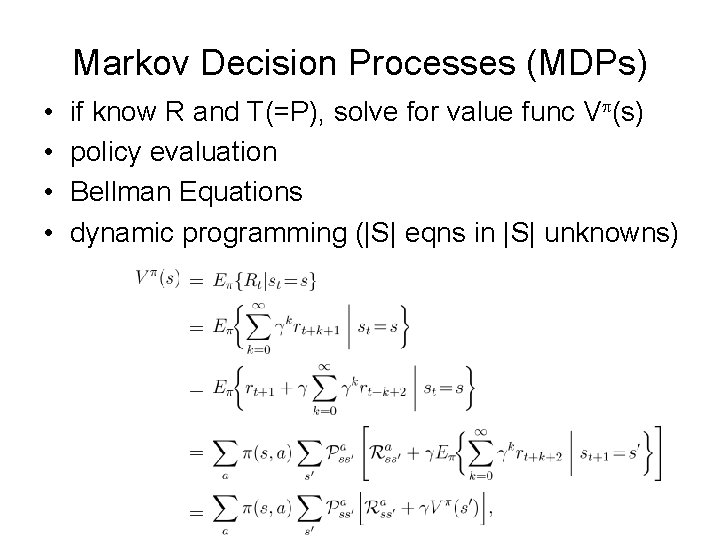
Markov Decision Processes (MDPs) • • if know R and T(=P), solve for value func Vp(s) policy evaluation Bellman Equations dynamic programming (|S| eqns in |S| unknowns)

MDPs • finding optimal policies • Value iteration – update V(s) iteratively until p(s)=argmaxa Vp(s) stops changing • Policy iteration – iterate between choosing p and updating V over all states • Monte Carlo sampling: run random scenarios using p and take average rewards as V(s)

Q-learning: model-free • Q-function: reformulate as value function of S and A, independent of R and T(=d)

Q-learning algorithm


Convergence • Theorem: Q converges to Q*, after visiting each state infinitely often (assuming |r|< ) • Proof: with each iteration (where all Sx. A visited), magnitude of largest error in Q table decreases by at least g

• “on-policy” Training – exploitation vs. exploration – will relevant parts of the space be explored if stick to current (sub-optimal) policy? – e-greedy policies: choose action with max Q value most of the time, or random action e % of the time • “off-policy” – learn from simulations or traces – SARSA: training example database: <s, a, r, s’, a’> • Actor-critic

Non-deterministic case

Temporal Difference Learning

• convergence is not the problem • representation of large Q table is the problem (domains with many states or continuous actions) • how to represent large Q tables? – neural network – function approximation – basis functions – hierarchical decomposition of state space
- Slides: 14