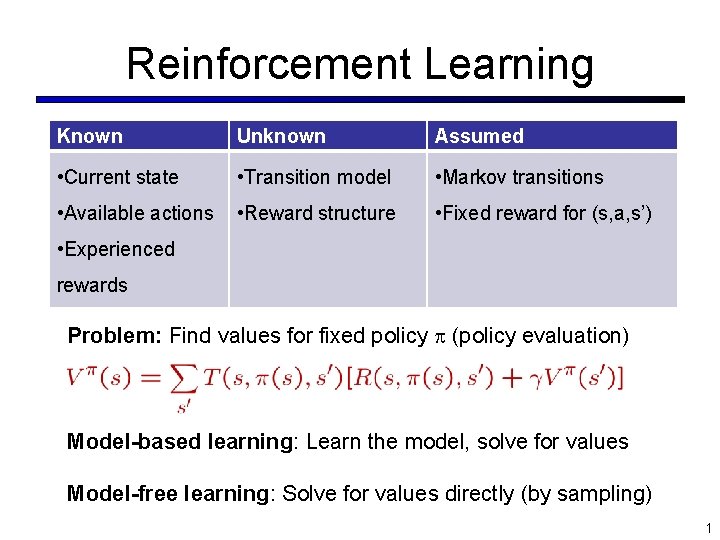
Reinforcement Learning Known Unknown Assumed Current state Transition

Reinforcement Learning Known Unknown Assumed • Current state • Transition model • Markov transitions • Available actions • Reward structure • Fixed reward for (s, a, s’) • Experienced rewards Problem: Find values for fixed policy (policy evaluation) Model-based learning: Learn the model, solve for values Model-free learning: Solve for values directly (by sampling) 1

The Story So Far: MDPs and RL Things we know how to do: Techniques: § If we know the MDP § Model-based DPs § Compute V*, Q*, * exactly § Evaluate a fixed policy § If we don’t know the MDP § We can estimate the MDP then solve § We can estimate V for a fixed policy § We can estimate Q*(s, a) for the optimal policy while executing an exploration policy § Value and policy Iteration § Policy evaluation § Model-based RL § Model-free RL: § Value learning § Q-learning 2

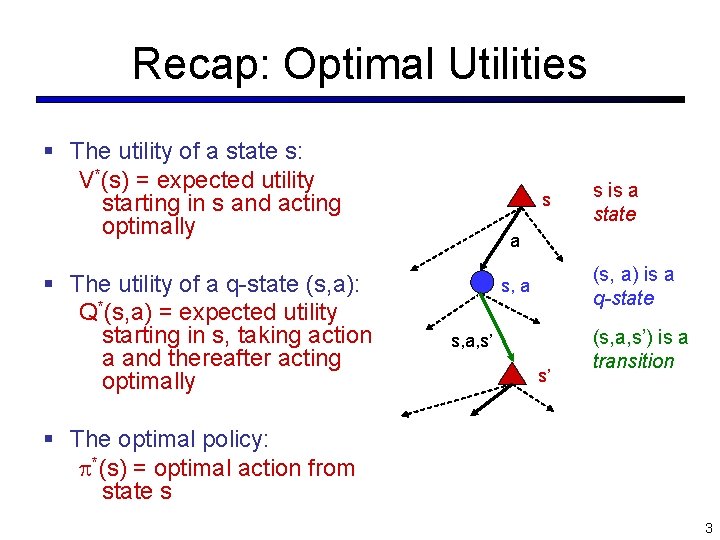
Recap: Optimal Utilities § The utility of a state s: V*(s) = expected utility starting in s and acting optimally § The utility of a q-state (s, a): Q*(s, a) = expected utility starting in s, taking action a and thereafter acting optimally s s is a state a (s, a) is a q-state s, a, s’ s’ (s, a, s’) is a transition § The optimal policy: *(s) = optimal action from state s 3

Temporal-Difference Learning § Big idea: learn from every experience! § Update V(s) each time we experience (s, a, s’, r) § Likely s’ will contribute updates more often s (s) s, (s) § Temporal difference learning § Policy still fixed! § Move values toward value of whatever successor occurs: running average! s’ Sample of V(s): Update to V(s): Same update: 5

Example: TD Policy Evaluation (1, 1) up -1 (1, 2) up -1 (1, 3) right -1 (2, 3) right -1 (3, 2) up -1 (4, 2) exit -100 (3, 3) right -1 (done) (4, 3) exit +100 (done) Take = 1, = 0. 5 7

Problems with TD Value Learning § TD value leaning is a model-free way to do policy evaluation § However, if we want to turn values into a (new) policy, we’re sunk: s a s, a, s’ s’ § Idea: learn Q-values directly § Makes action selection model-free too! 8

Active Learning § Full reinforcement learning § § § You don’t know the transitions T(s, a, s’) You don’t know the rewards R(s, a, s’) You can choose any actions you like Goal: learn the optimal policy … what value iteration did! § In this case: § Learner makes choices! § Fundamental tradeoff: exploration vs. exploitation § This is NOT offline planning! You actually take actions in the world and find out what happens… 9

Model-Based Active Learning § In general, want to learn the optimal policy, not evaluate a fixed policy § Idea: adaptive dynamic programming § Learn an initial model of the environment: § Solve for the optimal policy for this model (value or policy iteration) § Refine model through experience and repeat § Crucial: we have to make sure we actually learn about all of the model 10

Example: Greedy ADP § Imagine we find the lower path to the good exit first § Some states will never be visited following this policy from (1, 1) § We’ll keep re-using this policy because following it never collects the regions of the model we need to learn the optimal policy ? ? 11

What Went Wrong? § Problem with following optimal policy for current model: § Never learn about better regions of the space if current policy neglects them ? ? § Fundamental tradeoff: exploration vs. exploitation § Exploration: must take actions with suboptimal estimates to discover new rewards and increase eventual utility § Exploitation: once the true optimal policy is learned, exploration reduces utility § Systems must explore in the beginning and exploit in the limit 12

Detour: Q-Value Iteration § Value iteration: find successive approx optimal values § Start with V 0*(s) = 0, which we know is right (why? ) § Given Vi*, calculate the values for all states for depth i+1: § But Q-values are more useful! § Start with Q 0*(s, a) = 0, which we know is right (why? ) § Given Qi*, calculate the q-values for all q-states for depth i+1: 13

Q-Learning § We’d like to do Q-value updates to each Q-state: § But can’t compute this update without knowing T, R § Instead, compute average as we go § Receive a sample transition (s, a, r, s’) § This sample suggests § But we want to average over results from (s, a) (Why? ) § So keep a running average 14

Q-Learning Properties § Will converge to optimal policy § If you explore enough (i. e. visit each q-state many times) § If you make the learning rate small enough § Basically doesn’t matter how you select actions (!) § Off-policy learning: learns optimal q-values, not the values of the policy you are following S E 15

Exploration / Exploitation § Several schemes forcing exploration § Simplest: random actions ( greedy) § Every time step, flip a coin § With probability , act randomly § With probability 1 - , act according to current policy § Regret: expected gap between rewards during learning and rewards from optimal action § Q-learning with random actions will converge to optimal values, but possibly very slowly, and will get low rewards on the way § Results will be optimal but regret will be large § How to make regret small? 16

Exploration Functions § When to explore § Random actions: explore a fixed amount § Better ideas: explore areas whose badness is not (yet) established, explore less over time § One way: exploration function § Takes a value estimate and a count, and returns an optimistic utility, e. g. (exact form not important) 17

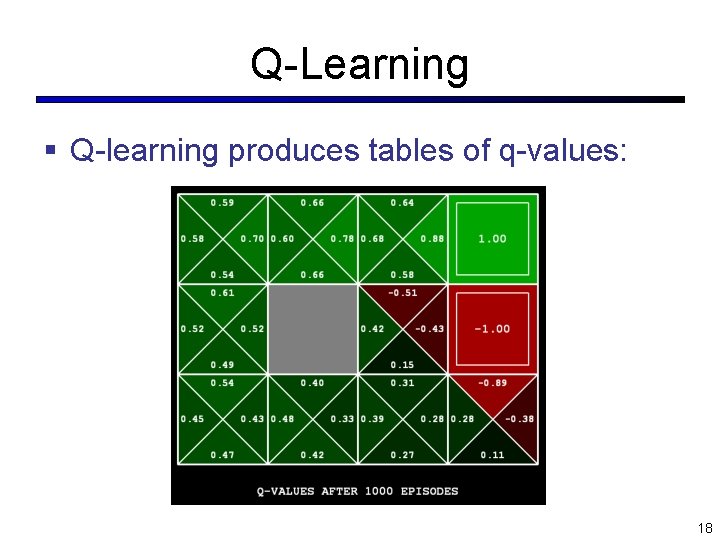
Q-Learning § Q-learning produces tables of q-values: 18

Q-Learning § In realistic situations, we cannot possibly learn about every single state! § Too many states to visit them all in training § Too many states to hold the q-tables in memory § Instead, we want to generalize: § Learn about some small number of training states from experience § Generalize that experience to new, similar states § This is a fundamental idea in machine learning, and we’ll see it over and over again 19

Example: Pacman § Let’s say we discover through experience that this state is bad: § In naïve q learning, we know nothing about this state or its q states: § Or even this one! 20

Feature-Based Representations § Solution: describe a state using a vector of features (properties) § Features are functions from states to real numbers (often 0/1) that capture important properties of the state § Example features: § § § § Distance to closest ghost Distance to closest dot Number of ghosts 1 / (dist to dot)2 Is Pacman in a tunnel? (0/1) …… etc. Is it the exact state on this slide? § Can also describe a q-state (s, a) with features (e. g. action moves closer to food) 21

Linear Feature Functions § Using a feature representation, we can write a q function (or value function) for any state using a few weights: § Advantage: our experience is summed up in a few powerful numbers § Disadvantage: states may share features but actually be very different in value! 22

Function Approximation § Q-learning with linear q-functions: Exact Q’s Approximate Q’s § Intuitive interpretation: § Adjust weights of active features § E. g. if something unexpectedly bad happens, disprefer all states with that state’s features § Formal justification: online least squares 23

Example: Q-Pacman 24

Linear Regression 40 26 24 22 20 20 30 40 20 0 0 Prediction 30 20 10 20 0 10 0 Prediction 25

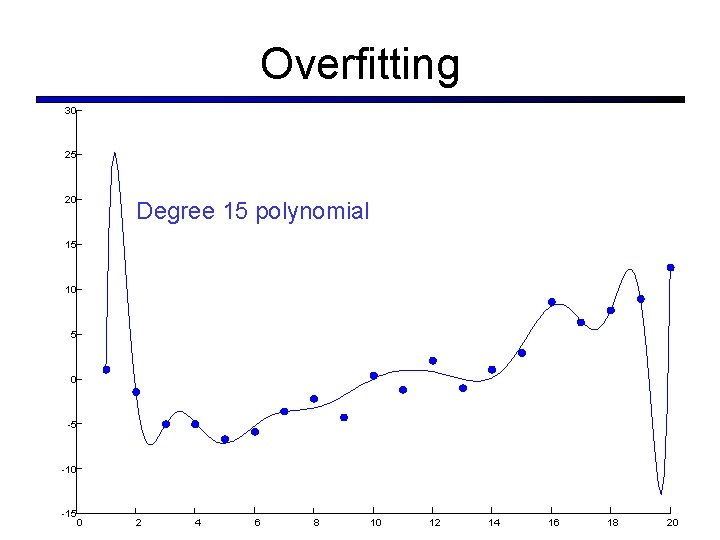
Overfitting 30 25 20 Degree 15 polynomial 15 10 5 0 -5 -10 -15 0 2 4 6 8 10 12 14 16 18 20

Policy Search 29

Policy Search § Problem: often the feature-based policies that work well aren’t the ones that approximate V / Q best § E. g. your value functions from project 2 were probably horrible estimates of future rewards, but they still produced good decisions § We’ll see this distinction between modeling and prediction again later in the course § Solution: learn the policy that maximizes rewards rather than the value that predicts rewards § This is the idea behind policy search, such as what controlled the upside-down helicopter 30

Policy Search § Simplest policy search: § Start with an initial linear value function or q-function § Nudge each feature weight up and down and see if your policy is better than before § Problems: § How do we tell the policy got better? § Need to run many sample episodes! § If there a lot of features, this can be impractical 31