Reinforcement Learning for Integer Programming Learning to Cut









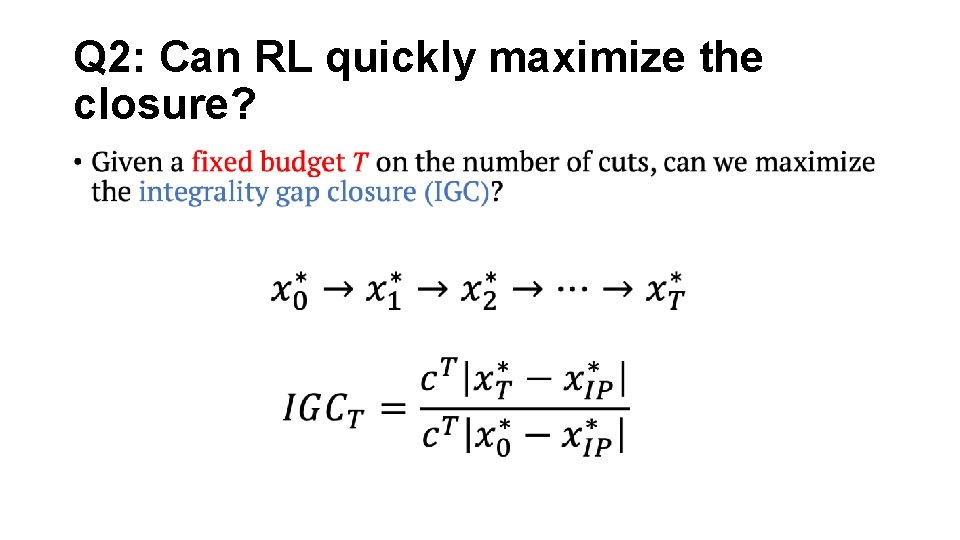



- Slides: 26

Reinforcement Learning for Integer Programming Learning to Cut Yunhao Tang

Thank you to my collaborators! Shipra Agrawal Yuri Faenza

Machine Learning (ML) for Combinatorial Optimization (CO) • How can ML help solve CO problem? • Directly predict the solutions? • Parameterization of the solutions, architecture… Pure ML based predictions • Neural architecture to mimic algorithmic computations? • ML flexibility + algorithmic inductive biases… • Combine ML with hard-coded algorithms • • Automate certain decision making of algorithms, replace heuristics Branch-and-bound [1, 2, 3] Primal heuristics [3] ML + Pure Cutting plane methods [4] classic algorithms Gasse et al, 2019; Zerpellon, et al, 2020; Nair et al, 2021; Tang et al, 2020

Why cutting plane methods? • Cutting planes are a backbone of modern commercial solvers • Agnostic to underlying problems • Very powerful: efficient algorithms for hard problems such as TSP • Challenge: no very well-established principle for cutting plane selection no good supervision • Branch-and-bound: FSB as supervised learning oracles [1, 2, 3] • Primal heuristics: solutions as supervised learning oracles [3] • Cutting plane: ? ? ? Gasse et al, 2019; Zerpellon, et al, 2020; Nair et al, 2021

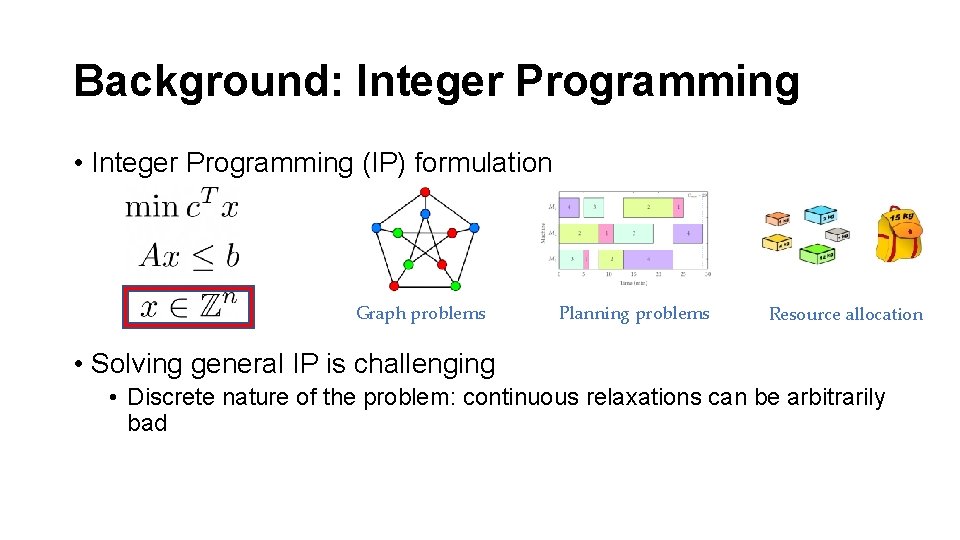
Background: Integer Programming • Integer Programming (IP) formulation Graph problems Planning problems Resource allocation • Solving general IP is challenging • Discrete nature of the problem: continuous relaxations can be arbitrarily bad

Cutting planes -- background • Main idea: solve the Linear Programming (LP) relaxations!

Cutting planes – what to learn • Cutting planes are generated from the relaxations • How to generate cuts? Gomory’s cuts [1] • Very general purpose – can be computed from the LP tableau • The procedure can be shown to terminate • The number of iterations (can be exponential ) depends on the sequence of cuts added • Can we learn which cutting plane to add to minimize the total efforts? Gomory, 1960

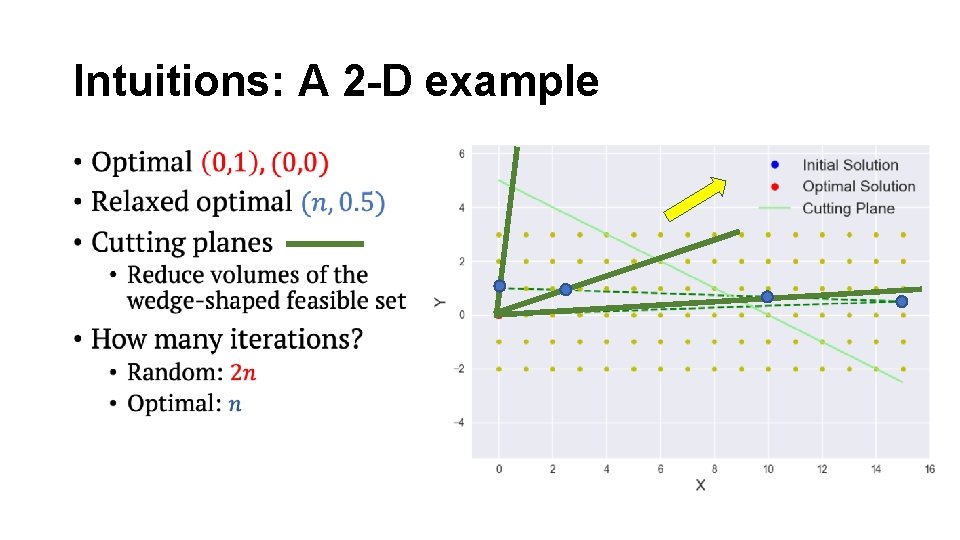
Intuitions: A 2 -D example •

Not an one-shot decision problem •

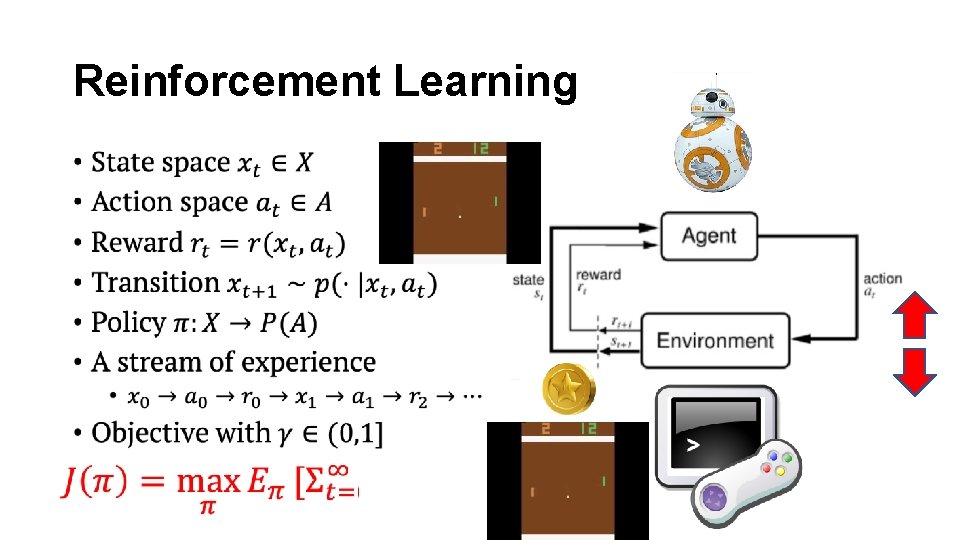
Reinforcement Learning •

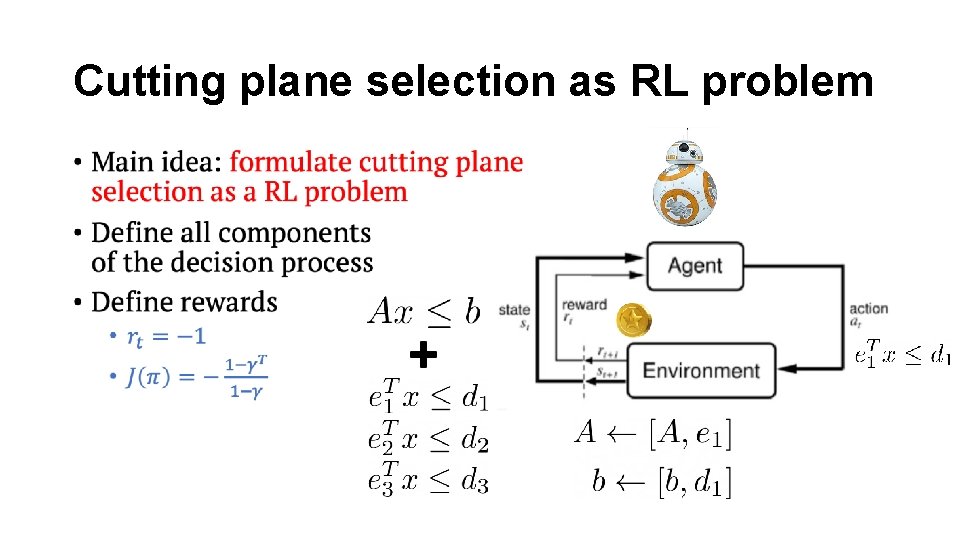
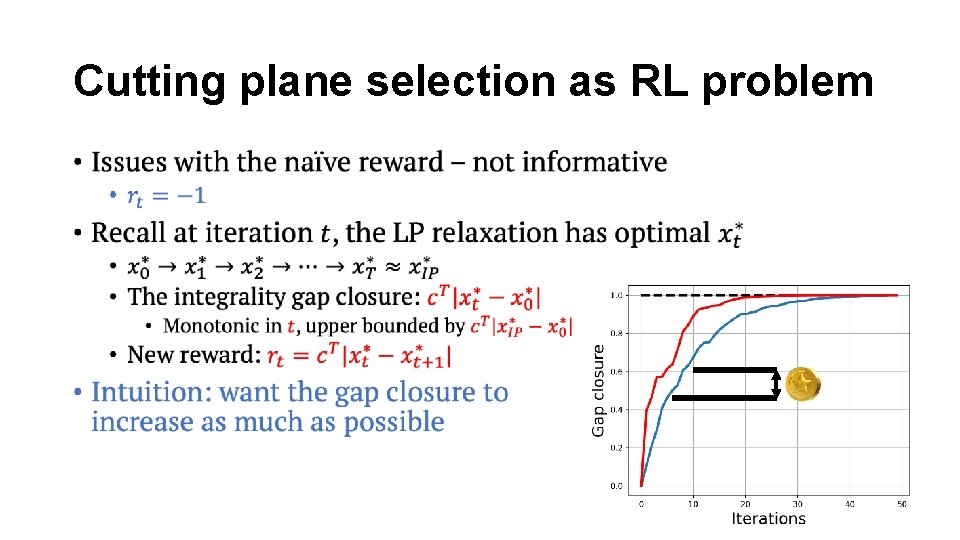
Cutting plane selection as RL problem •

Cutting plane selection as RL problem •

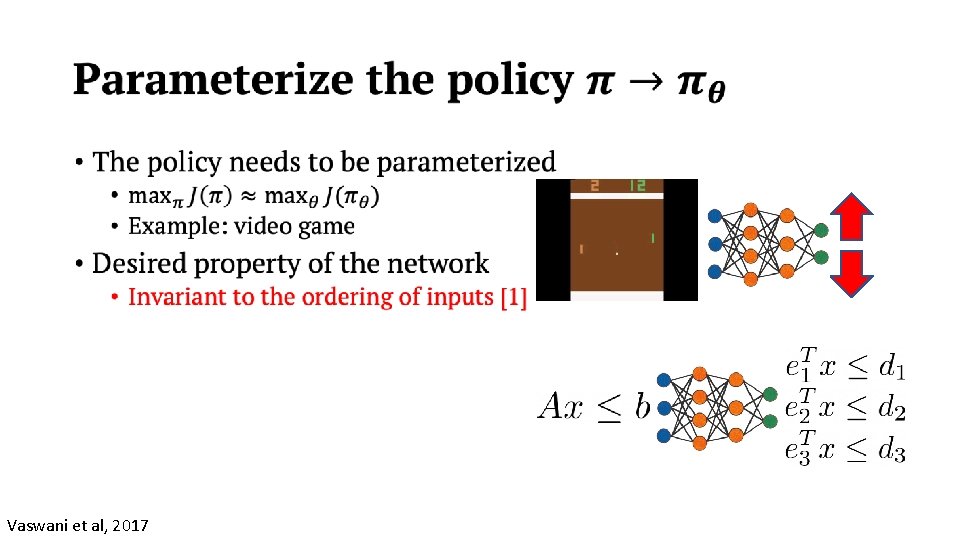
• Vaswani et al, 2017

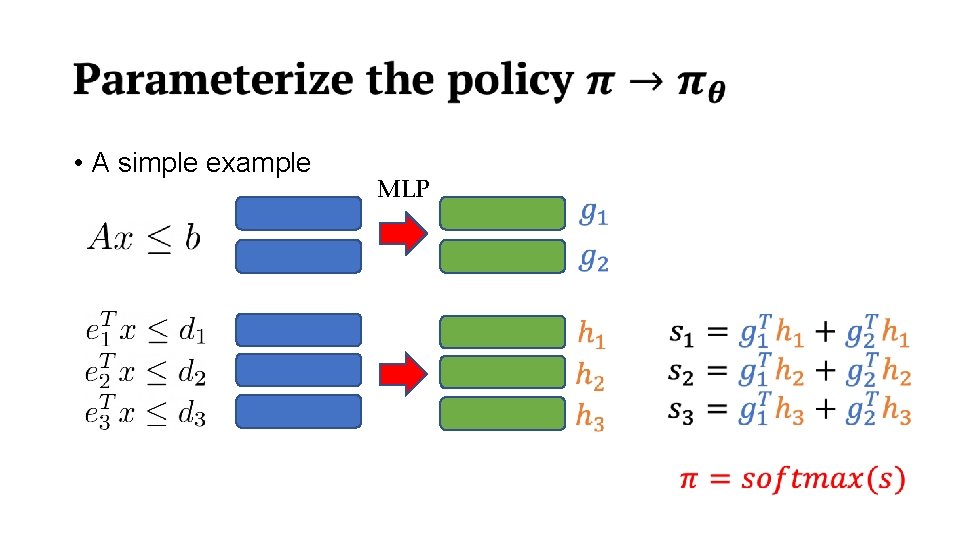
• A simple example MLP

Optimize the policy • Salisman et al, 2015; Mania et al, 2018

Experiment results • Wesselmann et al, 2012; Gomory, 1960

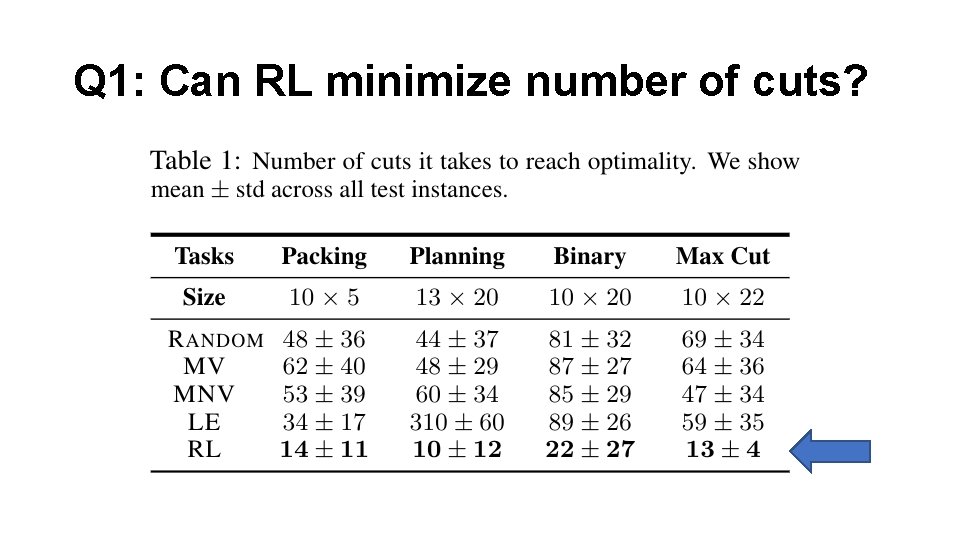
Q 1: Can RL minimize number of cuts?
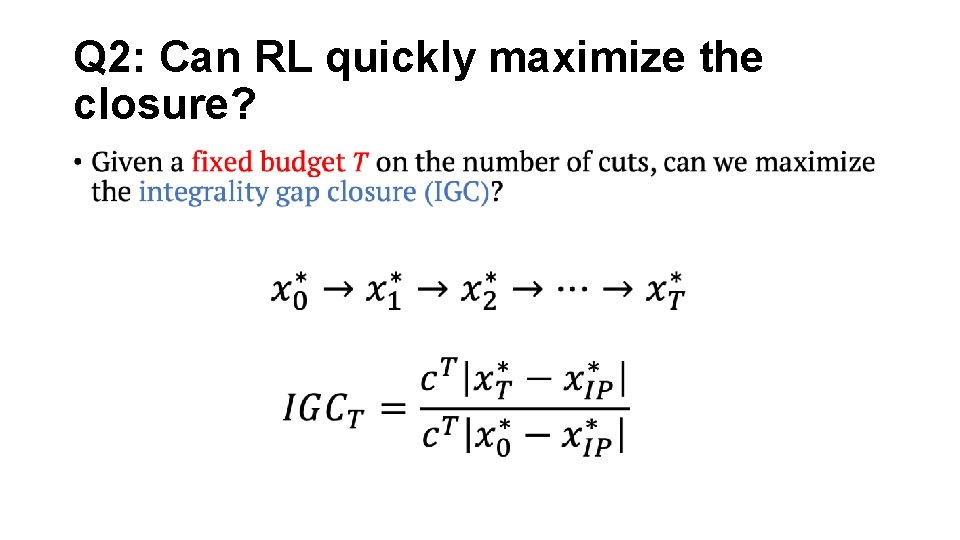
Q 2: Can RL quickly maximize the closure? •

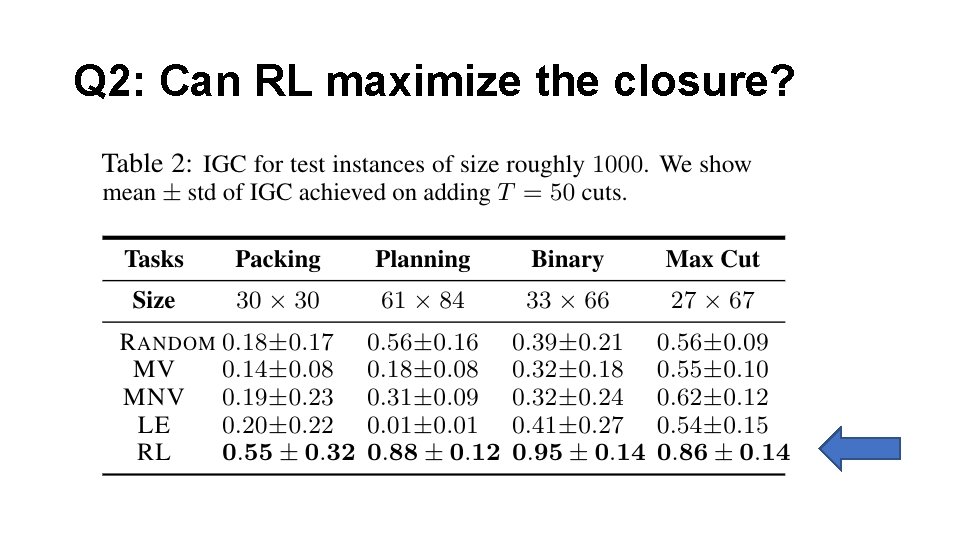
Q 2: Can RL maximize the closure?

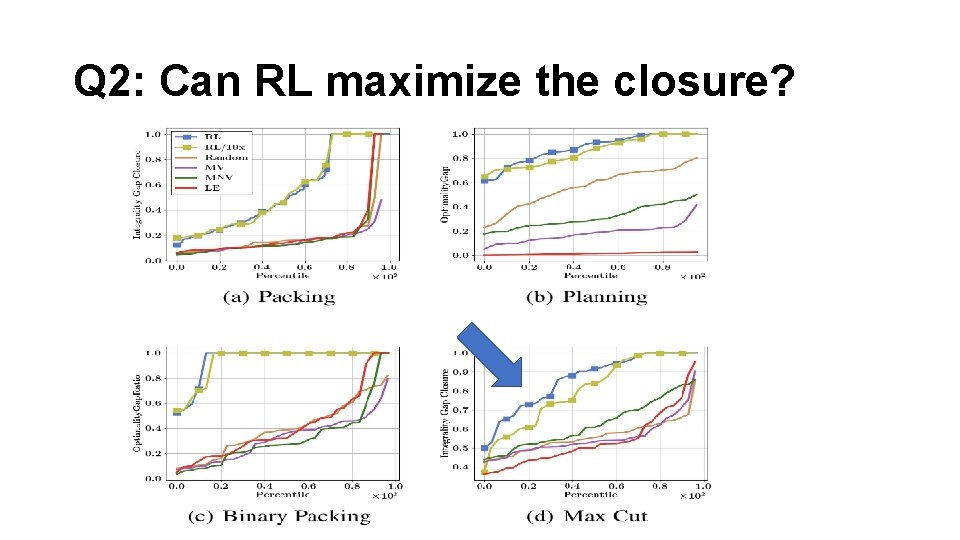
Q 2: Can RL maximize the closure?

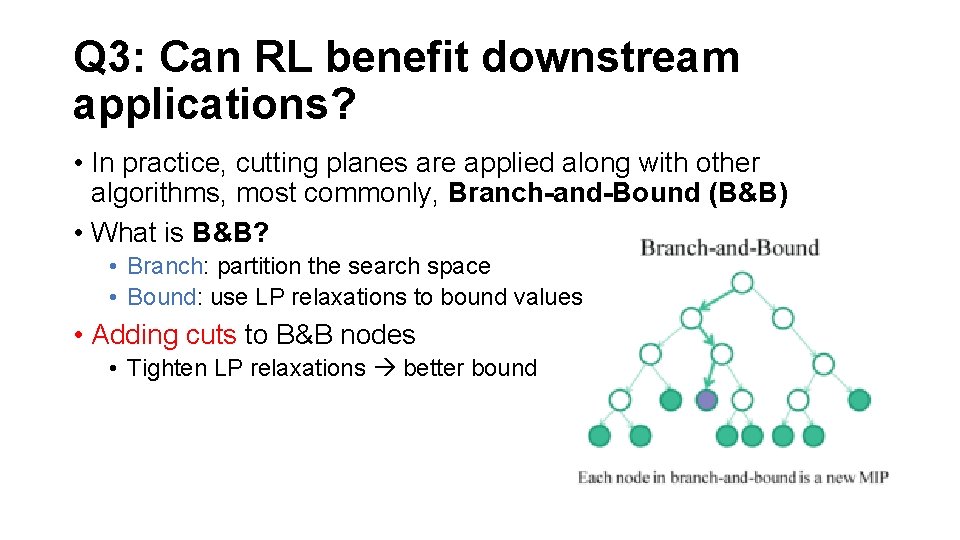
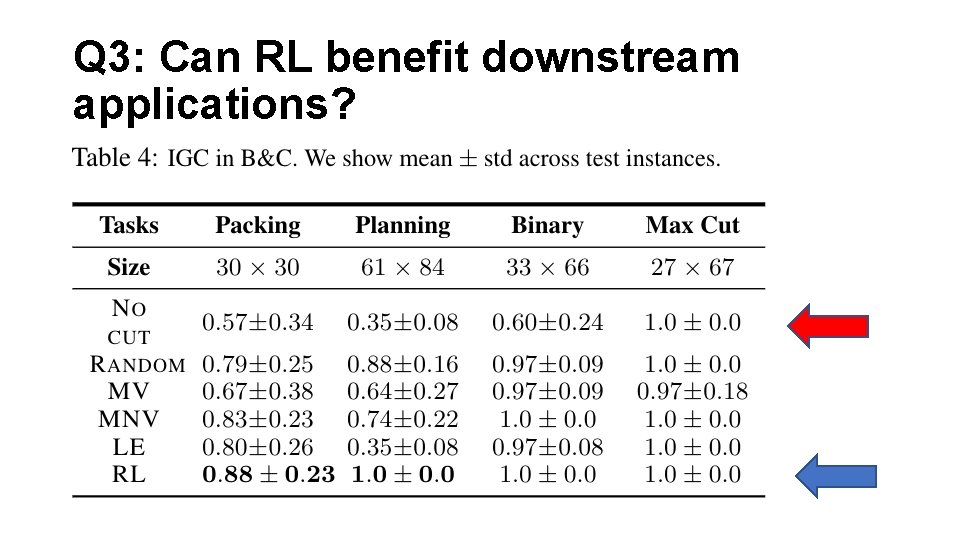
Q 3: Can RL benefit downstream applications? • In practice, cutting planes are applied along with other algorithms, most commonly, Branch-and-Bound (B&B) • What is B&B? • Branch: partition the search space • Bound: use LP relaxations to bound values • Adding cuts to B&B nodes • Tighten LP relaxations better bound

Q 3: Can RL benefit downstream applications? • Measure progress in a B&B tree • Step 1: Train cutting plane RL agent with cutting plane objective – without knowledge about downstream applications • Step 2: Directly test with B&B

Q 3: Can RL benefit downstream applications?

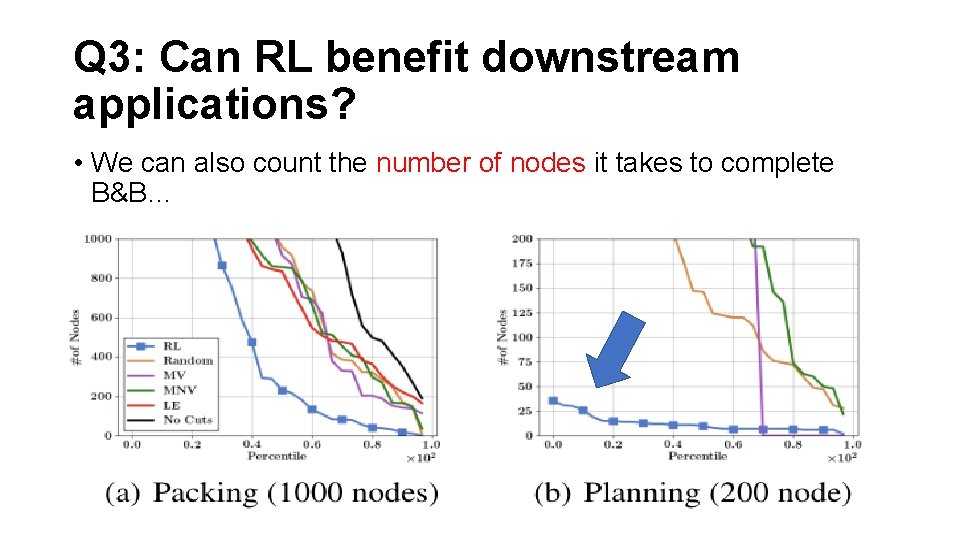
Q 3: Can RL benefit downstream applications? • We can also count the number of nodes it takes to complete B&B…

Summary • We formulate cutting plane selection as a RL problem • We can train RL agents that out-perform human-designed heuristics • Limitation: • Problems are relatively small scale… • Add only one cut at a time… • Future: RL for other IP algorithmic components?

Thank you for your attention! Please check out the full paper RL for IP: Learning to Cut, ICML 2020