Regulatory Motif Finding Finding Regulatory Motifs Given a

(Regulatory-) Motif Finding

Finding Regulatory Motifs . . . Given a collection of genes with common expression, Find the TF-binding motif in common

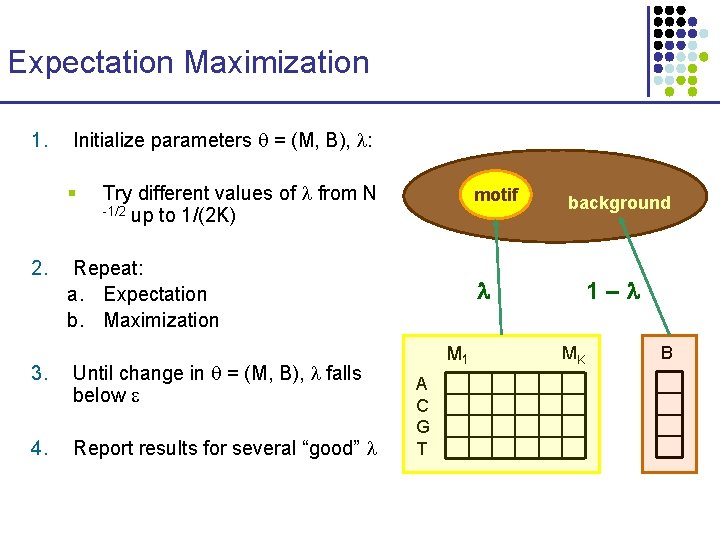
Expectation Maximization 1. Initialize parameters = (M, B), : § 2. Try different values of from N -1/2 up to 1/(2 K) motif Repeat: a. Expectation b. Maximization 3. Until change in = (M, B), falls below 4. Report results for several “good” background 1– M 1 A C G T MK B

Gibbs Sampling in Motif Finding

Gibbs Sampling • Given: § x 1, …, x. N, § motif length K, § background B, • Find: § Model M § Locations a 1, …, a. N in x 1, …, x. N Maximizing log-odds likelihood ratio:

Gibbs Sampling • • Align. ACE: first statistical motif finder Bio. Prospector: improved version of Align. ACE Algorithm (sketch): 1. Initialization: a. Select random locations in sequences x 1, …, x. N b. Compute an initial model M from these locations 2. Sampling Iterations: a. Remove one sequence xi b. Recalculate model c. Pick a new location of motif in xi according to probability the location is a motif occurrence

Gibbs Sampling Initialization: • Select random locations a 1, …, a. N in x 1, …, x. N • For these locations, compute M: • That is, Mkj is the number of occurrences of letter j in motif position k, over the total

Gibbs Sampling Predictive Update: • Select a sequence x = xi • Remove xi, recompute model: where j are pseudocounts to avoid 0 s, and B = j j M

Gibbs Sampling: For every K-long word xj, …, xj+k-1 in x: Qj = Prob[ word | motif ] = M(1, xj) … M(k, xj+k-1) Pi = Prob[ word | background ] B(xj) … B(xj+k-1) Let Prob 0 Sample a random new position ai according to the probabilities A 1, …, A|x|-k+1. |x|

Gibbs Sampling Running Gibbs Sampling: 1. Initialize 2. Run until convergence 3. Repeat 1, 2 several times, report common motifs

Advantages / Disadvantages • Very similar to EM Advantages: • Easier to implement • Less dependent on initial parameters • More versatile, easier to enhance with heuristics Disadvantages: • More dependent on all sequences to exhibit the motif • Less systematic search of initial parameter space

Repeats, and a Better Background Model • Repeat DNA can be confused as motif § Especially low-complexity CACACA… AAAAA, etc. Solution: more elaborate background model 0 th order: B = { p. A, p. C, p. G, p. T } 1 st order: B = { P(A|A), P(A|C), …, P(T|T) } … Kth order: B = { P(X | b 1…b. K); X, bi {A, C, G, T} } Has been applied to EM and Gibbs (up to 3 rd order)

Phylogenetic Footprinting (Slides by Martin Tompa)

Phylogenetic Footprinting (Tagle et al. 1988) • Functional sequences evolve slower than nonfunctional ones • Consider a set of orthologous sequences from different species • Identify unusually well conserved regions

Substring Parsimony Problem Given: • phylogenetic tree T, • set of orthologous sequences at leaves of T, • length k of motif • threshold d Problem: • Find each set S of k-mers, one k-mer from each leaf, such that the “parsimony” score of S in T is at most d. This problem is NP-hard.

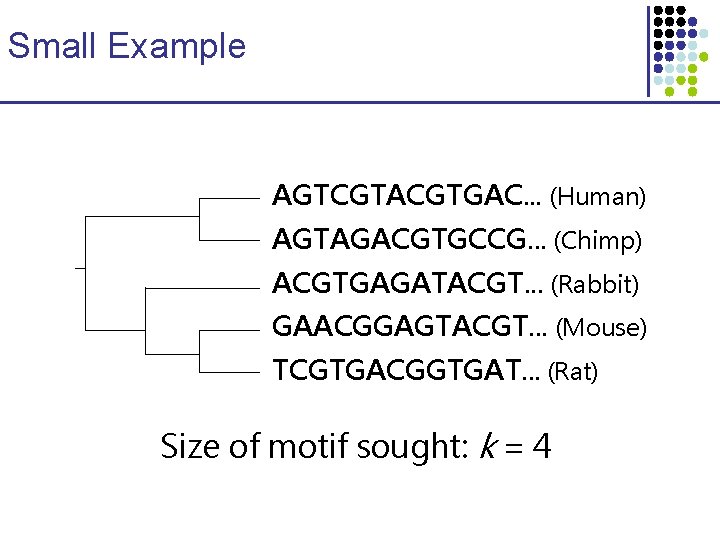
Small Example AGTCGTACGTGAC. . . (Human) AGTAGACGTGCCG. . . (Chimp) ACGTGAGATACGT. . . (Rabbit) GAACGGAGTACGT. . . (Mouse) TCGTGACGGTGAT. . . (Rat) Size of motif sought: k = 4

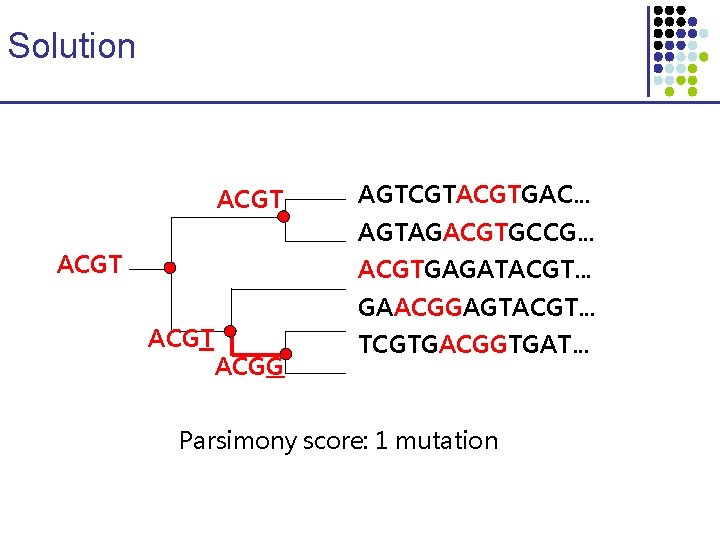
Solution ACGT AGTCGTACGTGAC. . . AGTAGACGTGCCG. . . ACGTGAGATACGT. . . ACGT GAACGGAGTACGT. . . ACGG TCGTGACGGTGAT. . . Parsimony score: 1 mutation

CLUSTALW multiple sequence alignment (rbc. S gene) Cotton Pea Tobacco Ice-plant Turnip Wheat Duckweed Larch ACGGTT-TCCATTGGATGA---AATGAGATAAGAT---CACTGTGC---TTCTTCCACGTG--GCAGGTTGCCAAAGATA-------AGGCTTTACCATT GTTTTT-TCAGTTAGCTTA---GTGGGCATCTTA----CACGTGGC---ATTATTATCCTA--TT-GGTGGCTAATGATA-------AGG--TTAGCACA TAGGAT-GAGATAAGATTA---CTGAGGTGCTTTA---CACGTGGC---ACCTCCATTGTG--GT-GACTTAAATGAAGA-------ATGGCTTAGCACC TCCCAT-ACATTGACATAT---ATGGCCCGCCTGCGGCAACAAAAA---AACTAAAGGATA--GCTAGTTGCTACTACAATTC--CCATAACTCACCACC ATTCAT-ATAAATAGAAGG---TCCGCGAACATTG--AAATGTAGATCATGCGTCAGAATT--GTCCTCTCTTAATAGGA-------GGAGC TATGAT-AAAATGAAATAT---TTTGCCCAGCCA-----ACTCAGTCGCATCCTCGGACAA--TTTGTTATCAAGGAACTCAC--CCAAAAACAAGCAAA TCGGAT-GGGGGGGCATGAACACTTGCAATCATT-----TCATGACTCATTTCTGAACATGT-GCCCTTGGCAACGTGTAGACTGCCAACATTAAA TAACAT-ATGATATAACAC---CGGGCACACATTCCTAAACAAAGAGTGATTTCAAATATATCGTTAATTACGACTAACAAAA--TGAAAGTACAAGACC Cotton Pea Tobacco Ice-plant Turnip Wheat Duckweed Larch CAAGAAAAGTTTCCACCCTC------TTTGTGGTCATAATG-GTT-GTAATGTC-ATCTGATTT----AGGATCCAACGTCACCCTTTCTCCCA-----A C---AAAACTTTTCAATCT-------TGTGTGGTTAATATG-ACT-GCAAAGTTTATCATTTTC----ACAATCCAACAA-ACTGGTTCT-----A AAAAATAATTTTCCAACCTTT---CATGTGTGGATATTAAG-ATTTGTATAATGTATCAAGAACC-ACATAATCCAATGGTTAGCTTTATTCCAAGATGA ATCACACATTCTTCCATTTCATCCCCTTTTTCTTGGATGAG-ATAAGATATGGGTTCCTGCCAC----GTGGCACCATGGTTTGTTA-ACGATAA CAAAAGCATTGGCTCAAGTTG-----AGACGAGTAACCATACACATTCATACGTTTTCTTACAAG-ATAAGATAATGTTATTTCT-----A GCTAGAAAAAGGTTGTGTGGCAGCCACCTAATGACATGAAGGACT-GAAATTTCCAGCACA-A-TGTATCCGACGGCAATGCTTCTTC-------ATATAATATTAGAAAAAAATC-----TCCCATAGTATTTACCAAAAGTCACACGACCA-CTAGACTCCAATTTACCCAAATCACTAACCAATT TTCTCGTATAAGGCCACCA-------TTGGTAGACACGTAGTATGCTAAATATGCACCACA-CTATCAGATATGGTAGTGGGATCTG--ACGGTCA Cotton Pea Tobacco Ice-plant Turnip Wheat Duckweed Larch ACCAATCTCT---AAATGTT----GTGAGCT---TAG-GCCAAATTT-TATGACTATA--TAT----AGGGGATTGCACC----AAGGCAGTG-ACACTA GGCAGTGGCC---AACTAC----------CACAATTT-TAAGACCATAA-TAT----TGGAAATAGAA------AAATCAAT--ACATTA GGGGGTTGTT---GATTTTT----GTCCGTTAGATAT-GCGAAATATGTAAAACCTTAT-CAT----TATAGAG------TGGTGGGCA-ACGATG GGCTCTTAATCAAAAGTTTTAGGTGTGAATTTAGTTT-GATGAGTTTTAAGGTCCTTAT-TATA---TATAGGAAGGGGG----TGCTATGGA-GCAAGG CACCTTTAATCCTGTGGCAGTTAACGACGATATCATGAAATCTTGATCCTTCGAT-CATTAGGGCTTCATACCTCT----TGCGCTTCTCACTATA CACTGATCCGGAGAAGATAAGGAAACGAGGCAACCAGCGAACGTGAGCCATCCCAACCA-CATCTGTACCAAAGAAACGG----GGCTATACCGTG TTAGGTTGAATGGAAAATAG---AACGCAATAATGTCCGACATATTTCCTATATTTCCG-TTTTTCGAGAGAAGGCCTGTGTACCGATAAGGATGTAATC CGCTTCTCCTCTGGAGTTATCCGATTGTAATCCTTGCAGTCCAATTTCTCTGGC-CCA----ACCTTAGAGATTG----GGGCTTATA-TCTATA Cotton Pea Tobacco Ice-plant Larch Turnip Wheat Duckweed T-TAAGGGATCAGTGAGAC-TCTTTTGTATAACTGTAGCAT--ATAGTAC TATAAAGCAAGTTTTAGTA-CAAGCTTTGCAATTCAACCAC--A-AGAAC CATAGACCATCTTGGAAGT-TTAAAGGGAAAAAAGGAAAAG--GGAGAAA TCCTCATCAAAAGGGAAGTGTTTTTTCTCTAACTATATTACTAAGAGTAC TCTTCTTCACAC---AATCCATTTGTGTAGAGCCGCTGGAAGGTAAATCA TATAGATAACCA---AAGCAATAGACAAGTTAAG-AGAAAAG GTGACCCGGCAATGGGGTCCTCAACTGTAGCCGGCATCCTCCTCC CATGGGGCGACG---CAGTGTGTGGAGGAGCAGGCTCAGTCTCCTTCTCG

An Exact Algorithm (generalizing Sankoff and Rousseau 1975) Wu [s] = best parsimony score for subtree rooted at node u, if u is labeled with string s. … 4 k entries … ACGG: 1 ACGT: 0. . . ACGG: + ACGT: 0. . . … ACGG: ACGT : 0. . . … ACGG: 2 ACGT: 1 … ACGG: ACGT : 0. . . … ACGG: 1 ACGT: 1. . . … ACGG: 0 ACGT: 2. . . … AGTCGTACGTG ACGGGACGTGC ACGTGAGATAC GAACGGAGTAC TCGTGACGGTG ACGG: 0 ACGT: + . . .

Running Time W u [ s] = O(k 42 k v: child of u ) time per node min ( Wv [t] + d(s, t) ) t Number of species Average sequence length Total time O(n k (42 k + l )) Motif length

Limits of Motif Finders 0 ? ? ? gene • Given upstream regions of coregulated genes: § Increasing length makes motif finding harder – random motifs clutter the true ones § Decreasing length makes motif finding harder – true motif missing in some sequences

Limits of Motif Finders A (k, d)-motif is a k-long motif with d random differences per copy Motif Challenge problem: Find a (15, 4) motif in N sequences of length L CONSENSUS, MEME, Align. ACE, & most other programs fail for N = 20, L = 1000

Example Application: Motifs in Yeast Group: Tavazoie et al. 1999, G. Church’s lab, Harvard Data: • Microarrays on 6, 220 m. RNAs from yeast Affymetrix chips (Cho et al. ) • 15 time points across two cell cycles

Processing of Data 1. Selection of 3, 000 genes Genes with most variable expression were selected 2. Clustering according to common expression • • • K-means clustering 30 clusters, 50 -190 genes/cluster Clusters correlate well with known function 3. Align. ACE motif finding • • 600 -long upstream regions 50 regions/trial

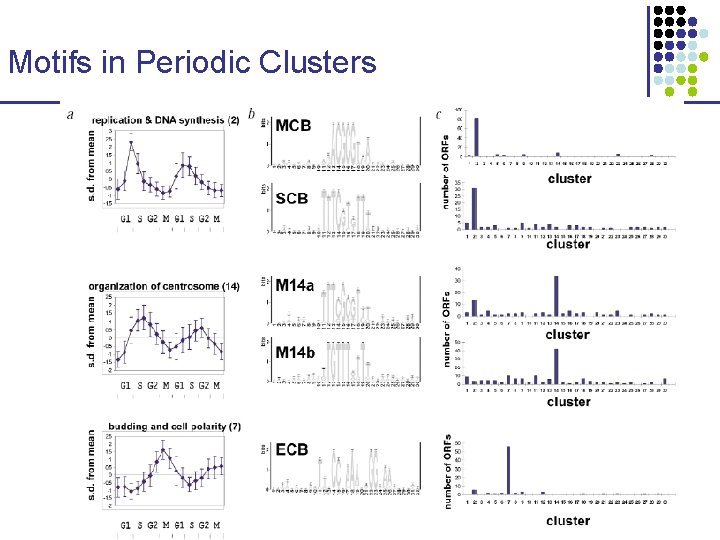
Motifs in Periodic Clusters

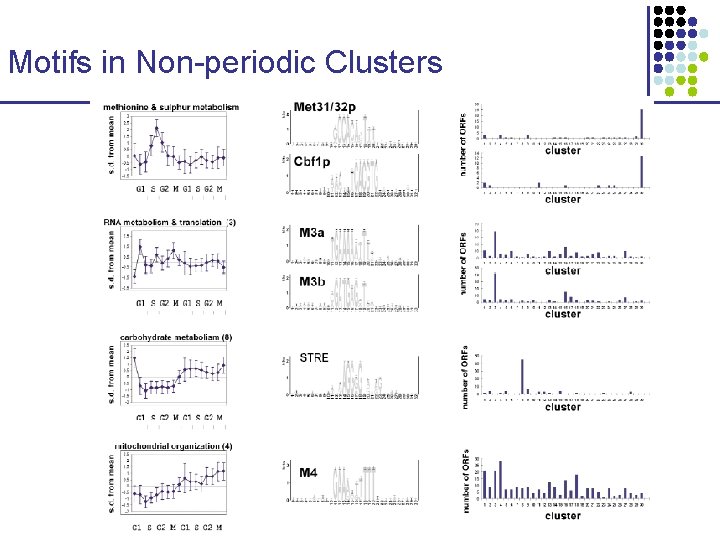
Motifs in Non-periodic Clusters

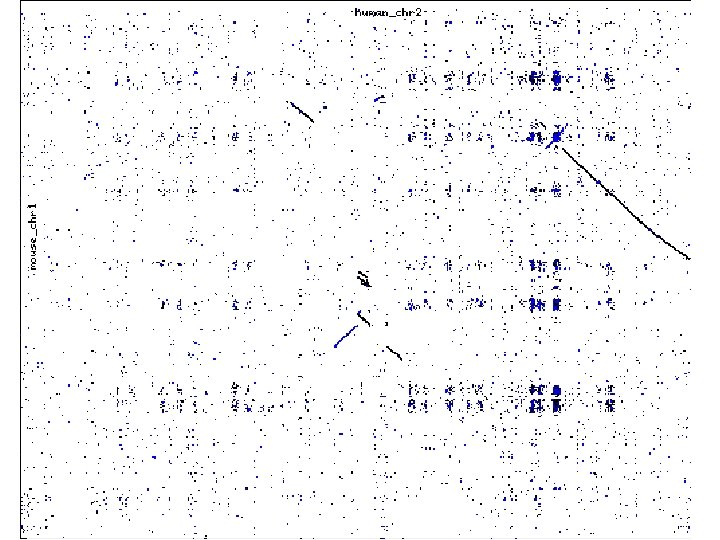
Rapid Global Alignments How to align genomic sequences in (more or less) linear time

Motivation • Genomic sequences are very long: § Human genome = 3 x 109 –long § Mouse genome = 2. 7 x 109 –long • Aligning genomic regions is useful for revealing common gene structure § Useful to compare regions > 1, 000 -long

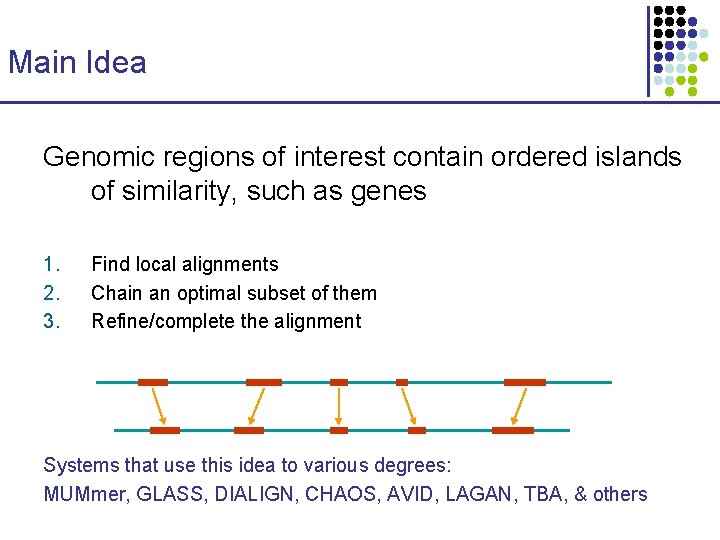
Main Idea Genomic regions of interest contain ordered islands of similarity, such as genes 1. 2. 3. Find local alignments Chain an optimal subset of them Refine/complete the alignment Systems that use this idea to various degrees: MUMmer, GLASS, DIALIGN, CHAOS, AVID, LAGAN, TBA, & others

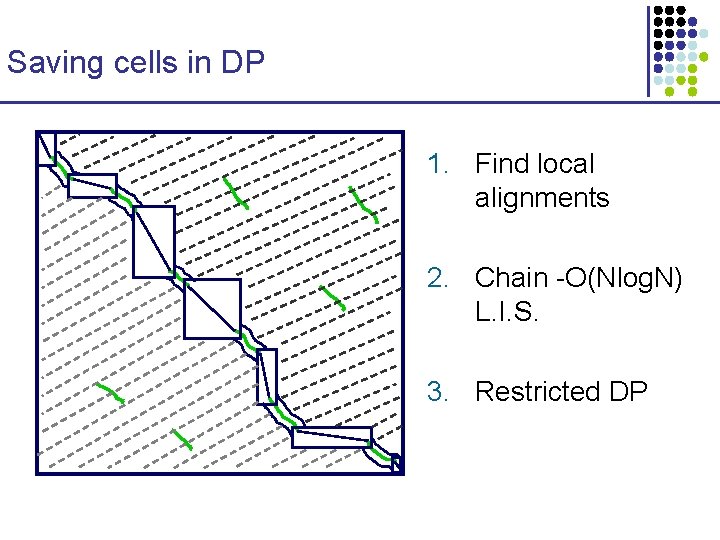
Saving cells in DP 1. Find local alignments 2. Chain -O(Nlog. N) L. I. S. 3. Restricted DP

Methods to CHAIN Local Alignments Sparse Dynamic Programming O(N log N)

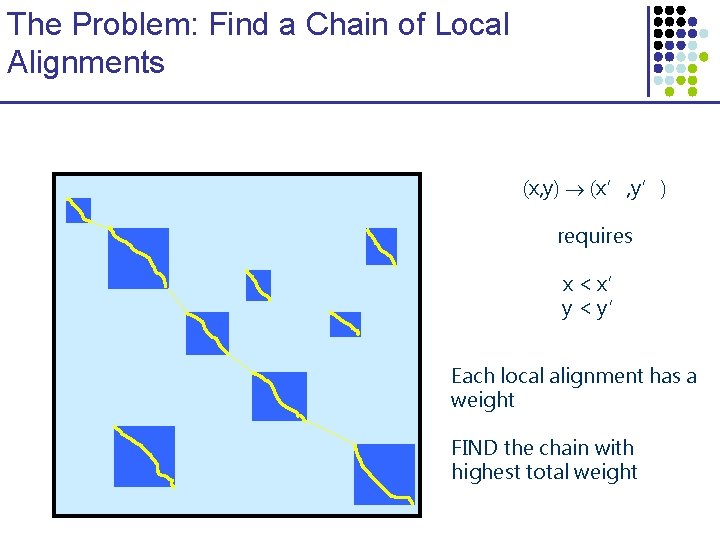
The Problem: Find a Chain of Local Alignments (x, y) (x’, y’) requires x < x’ y < y’ Each local alignment has a weight FIND the chain with highest total weight

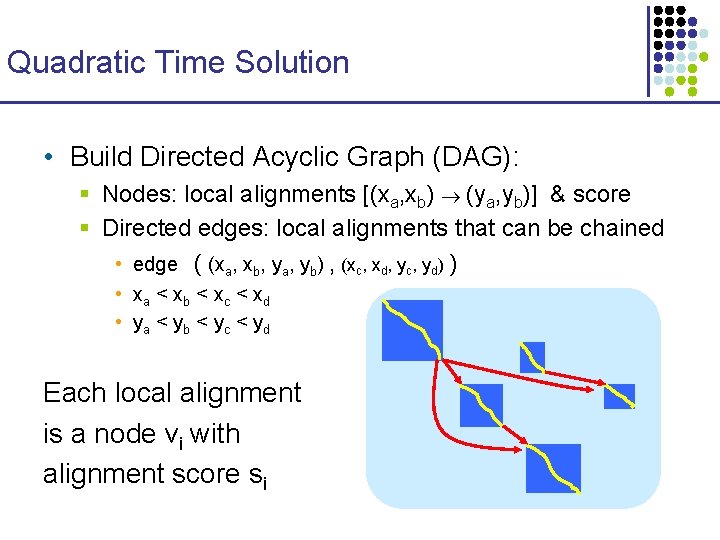
Quadratic Time Solution • Build Directed Acyclic Graph (DAG): § Nodes: local alignments [(xa, xb) (ya, yb)] & score § Directed edges: local alignments that can be chained • edge ( (xa, xb, ya, yb) , (xc, xd, yc, yd) ) • xa < xb < xc < xd • ya < yb < yc < yd Each local alignment is a node vi with alignment score si

Quadratic Time Solution Dynamic programming: Initialization: Find each node va s. t. there is no edge (u, v 0) Set score of V(a) to be sa Iteration: For each vi, optimal path ending in vi has total score: V(i) = max ( weight(vj, vi) + V(j) ) Termination: Optimal global chain: j = argmax ( V(j) ); trace chain from vj Worst case time: quadratic

Sparse Dynamic Programming Back to the LCS problem: • Given two sequences § x = x 1, …, xm § y = y 1, …, yn • Find the longest common subsequence § Quadratic solution with DP • How about when “hits” xi = yj are sparse?

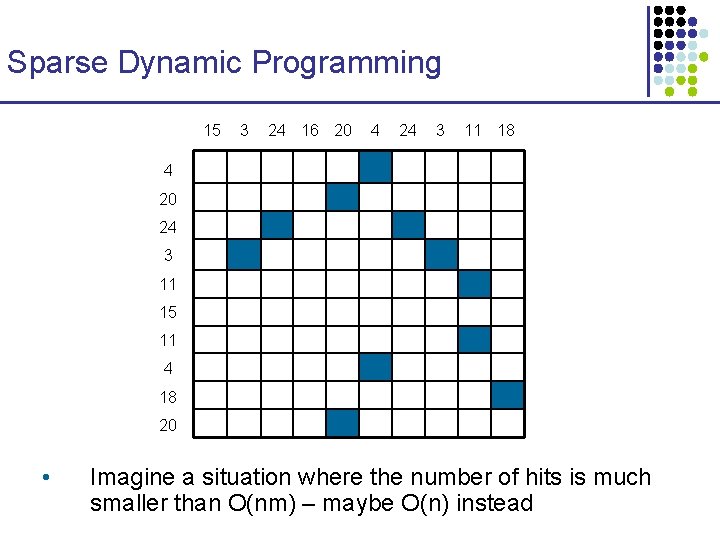
Sparse Dynamic Programming 15 3 24 16 20 4 24 3 11 18 4 20 24 3 11 15 11 4 18 20 • Imagine a situation where the number of hits is much smaller than O(nm) – maybe O(n) instead

Sparse Dynamic Programming – L. I. S. • Longest Increasing Subsequence • Given a sequence over an ordered alphabet § x = x 1, …, xm • Find a subsequence § s = s 1, …, sk § s 1 < s 2 < … < sk

Sparse LCS expressed as LIS x Create a sequence w • • • Every matching point x-to-y, (i, j), is inserted into a sequence as follows: For each position j of x, from smallest to largest, insert in z the points (i, j), in decreasing column i order The 11 example points are inserted in the order given 15 3 24 16 20 Any two points (ya, xa), (yb, xb) can be chained iff § a is before b in w, and § ya < yb 3 11 18 4 20 2 y 24 7 1 8 11 10 15 9 11 5 4 • 24 6 4 3 4 11 18 20 3

Sparse LCS expressed as LIS x Create a sequence w w = (4, 2) (3, 3) (10, 5) (2, 5) (8, 6) (1, 6) (3, 7) (4, 8) (7, 9) (5, 9) (9, 10) 15 3 • (ya, xa) < (yb, xb) if ya < yb Claim: An increasing subsequence of w is a common subsequence of x and y 24 3 11 18 4 20 3 4 6 4 2 y 24 Consider now w’s elements as ordered lexicographically, where 24 16 20 7 1 8 11 10 15 9 11 5 4 11 18 20 3

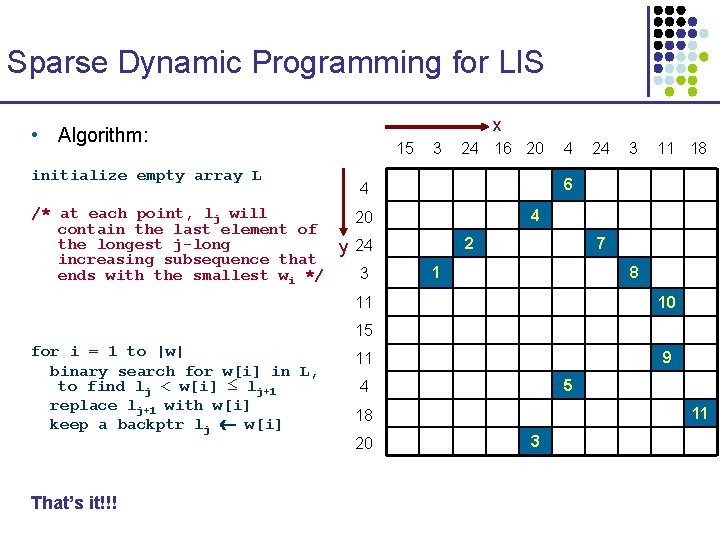
Sparse Dynamic Programming for LIS x • Algorithm: initialize empty array L 15 3 24 16 20 24 3 11 18 6 4 /* at each point, lj will 20 contain the last element of the longest j-long y 24 increasing subsequence that 3 ends with the smallest wi */ 4 4 2 7 1 8 11 10 15 for i = 1 to |w| binary search for w[i] in L, to find lj < w[i] ≤ lj+1 replace lj+1 with w[i] keep a backptr lj w[i] That’s it!!! 9 11 5 4 11 18 20 3

Sparse Dynamic Programming for LIS x Example: w = (4, 2) (3, 3) (10, 5) (2, 5) (8, 6) (1, 6) (3, 7) (4, 8) (7, 9) (5, 9) (9, 10) L= 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. (4, 2) (3, 3) (10, 5) (2, 5) (8, 6) (1, 6) (3, 7) (4, 8) (7, 9) (1, 6) (3, 7) (4, 8) (5, 9) (9, 10) 15 3 24 16 20 24 3 11 18 6 4 4 20 2 y 24 3 4 7 1 8 11 10 15 9 11 5 4 11 18 20 3 Longest common subsequence: s = 4, 24, 3, 11, 18

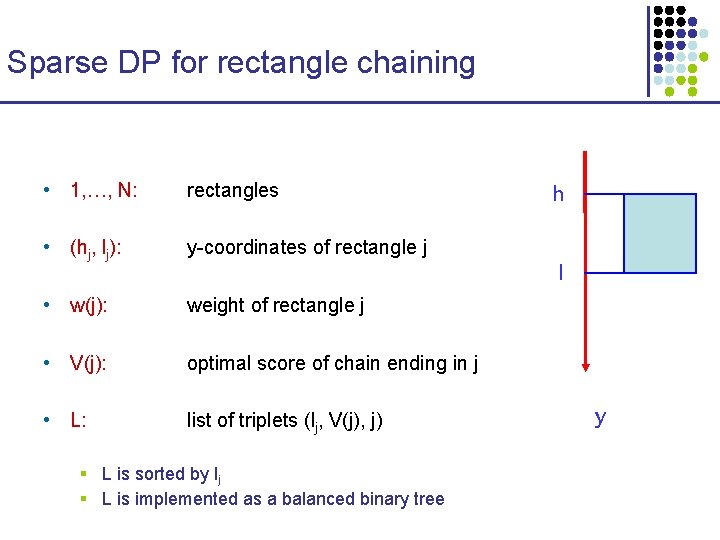
Sparse DP for rectangle chaining • 1, …, N: rectangles • (hj, lj): y-coordinates of rectangle j • w(j): weight of rectangle j • V(j): optimal score of chain ending in j • L: list of triplets (lj, V(j), j) § L is sorted by lj § L is implemented as a balanced binary tree h l y

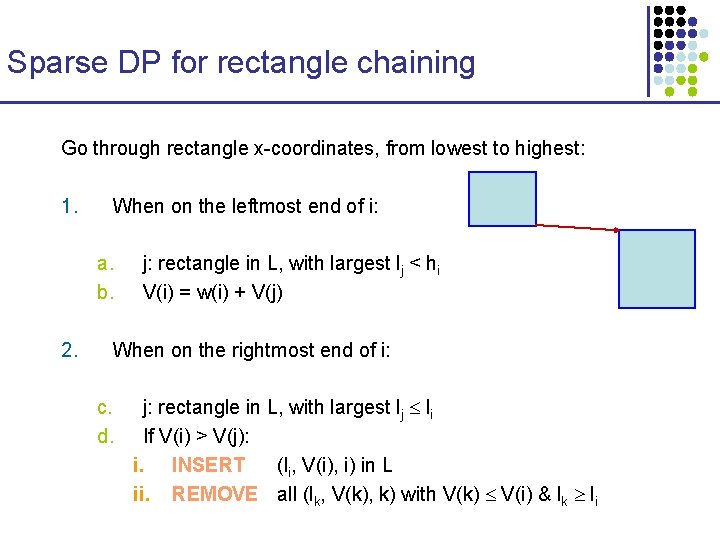
Sparse DP for rectangle chaining Go through rectangle x-coordinates, from lowest to highest: 1. When on the leftmost end of i: a. b. 2. j: rectangle in L, with largest lj < hi V(i) = w(i) + V(j) When on the rightmost end of i: c. d. j: rectangle in L, with largest lj li If V(i) > V(j): i. INSERT (li, V(i), i) in L ii. REMOVE all (lk, V(k), k) with V(k) V(i) & lk li

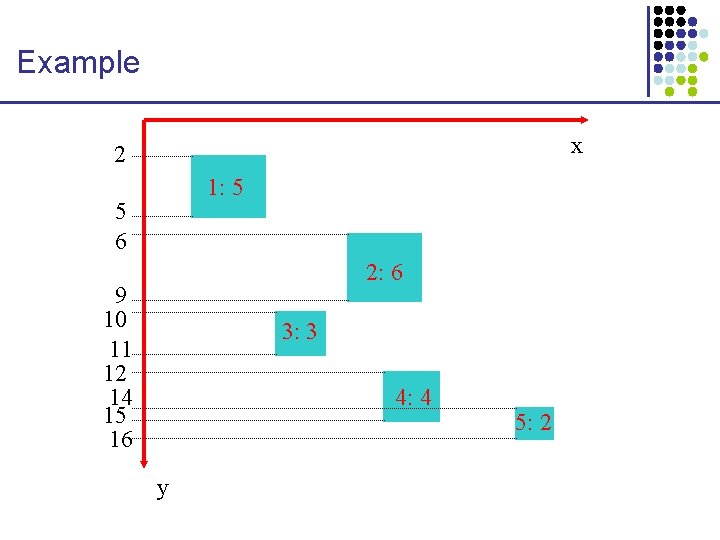
Example x 2 1: 5 5 6 2: 6 9 10 11 12 14 15 16 3: 3 4: 4 y 5: 2

Time Analysis 1. Sorting the x-coords takes O(N log N) 2. Going through x-coords: N steps 3. Each of N steps requires O(log N) time: 1. 2. 3. 4. Searching L takes log N Inserting to L takes log N All deletions are consecutive, so log N per deletion Each element is deleted at most once: N log N for all deletions 1. Recall that INSERT, DELETE, SUCCESSOR, take O(log N) time in a balanced binary search tree