Regularizing Irregularity Bitmapbased and Portable Sparse Matrix Multiplication

Regularizing Irregularity: Bitmap-based and Portable Sparse Matrix Multiplication for Graph Data on GPUs Jianting Zhang 1, Le Gruenwald 2 jzhang@cs. ccny. cuny. edu http: //www-cs. ccny. cuny. edu/~jzhang/ 1 The City College of New York 2 University of Oklahoma

Outline • Introduction, Background & Motivation • The Proposed bm. SPARSE Technique • • bm. SPARSE format for Sparse Matrix Generating Task List in Sp. GEMM Block Multiplication Compaction • Experiments and Results on Web. Base-1 M Dataset • Conclusion and Future Work

Introduction & Background • Graph data are becoming increasingly important in real world applications • Graphs can be naturally represented as sparse matrices; relationship between graph algorithms and linear algebra algorithms is well understood • There are increasing interests in utilizing sparse matrix operations for graph applications • Dozens of sparse matrix storage formats have been proposed • Coordinate list (COO) • Compressed Sparse Row (CSR) • Most of them are evaluated for Sparse Matrix-Vector Multiplication(Sp. MV) nv. GRAPH example of using CSR sparse matrix format for creating and manipulating a graph

Background & Motivation • Existing Sparse General Matrix-Matrix Multiplication (Sp. GEMM) techniques are based on COO/CSR • Efficient Sp. GEMM is more challenging than Sp. MV: • a large two-dimensional matrix is more complex than a vector (or multiple vectors) • involves two input matrices and needs to handle sparsity/irregularity on both sides • Data access costs due to irregular data layout may dominate over FLOPS • Classic sparse matrix data formats are not suitable for new hardware: • Google TPU and Nvidia Volta Tensor Core: highly efficient parallel units for small dense matrix multiplication (256*256/16*16) • COO: finest granularity, large memory footprint, spatial adjacency unutilized • CSR: typically segmenting at row/multi-row level slim rectangles Question: are there alternative sparse matrix formats that can be used to efficiently support Sp. GEMM for graph data, considering newly emerging parallel hardware? Will the classic bitmap indexing technique help Sp. GEMM? https: //www. nvidia. co m/en-us/datacenter/tensorcore/ 640 tensor cores (8 per SM), each process 4*4 matrix; work in warps to process 16*16 matrix

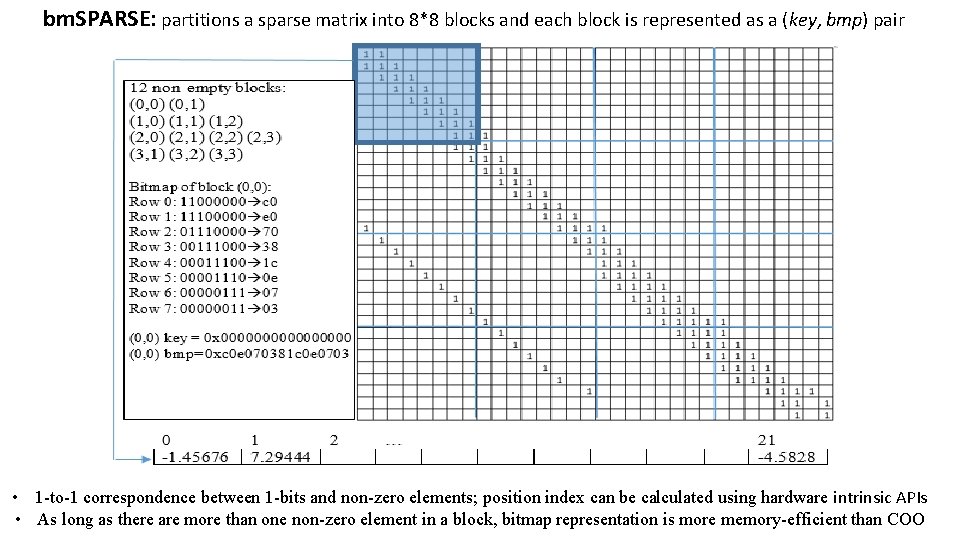
bm. SPARSE: partitions a sparse matrix into 8*8 blocks and each block is represented as a (key, bmp) pair • 1 -to-1 correspondence between 1 -bits and non-zero elements; position index can be calculated using hardware intrinsic APIs • As long as there are more than one non-zero element in a block, bitmap representation is more memory-efficient than COO

bm. SPARSE: Cik=sum(Aij*Bjk) 1. Data Parallel Generation of Task List in Sp. GEMM • A task multiplies two input 8*8 blocks and generates an 8*8 output block • Regularizing irregularity: all tasks can be executed in parallel and their workloads are bounded • Pairing blocks and generating a task list can be considered as a special join problem : (i, k)=>{j} • Using data parallel primitives to balance between efficiency and portability 2. Block Multiplication • Native CUDA implementation on Nvidia GPUs (8*8 threads per block) • Each threads aij and bjk from a (a, b) pair and increases cik by aij* bjk before the final output, all in parallel • Using __popcll and __ballot GPU intrinsic functions for efficiency 3. Compaction on zeros for final output • Each output block has at most 8*8 non-zero values; zero elements can be compacted within a block in Step 2 but requires extra efforts to compact them across blocks • Two-phase approach: the first phase counts the numbers and positions of non-zero elements for all blocks and allocate memory while the non-zero elements are actually output in the 2 nd phase after re-computation

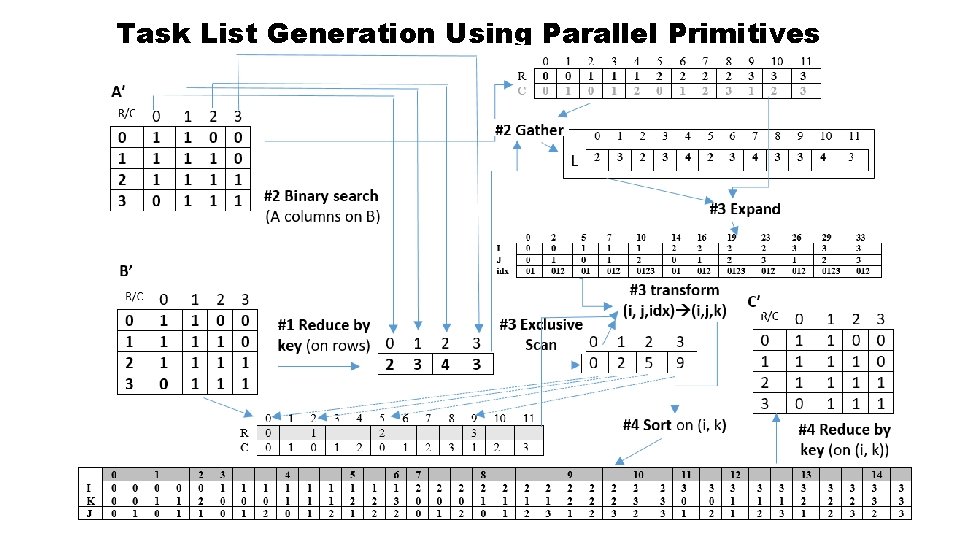
Task List Generation Using Parallel Primitives

Experiments and Results • Web. Base-1 M dataset from University of Florida (UFL) Sparse Matrix Collection. has 1, 000, 005 rows (n_row) and 1, 000, 005 columns (n_col) and 3, 105, 536 non-zero values (nnz) • C=A*A • Baselines for comparison: CUSP, bh. SPARSE • Hardware 1 (paper): • 2013 Nvidia GTX Titan (Kepler) GPU with 2, 688 CUDA cores and 6 GB GDDR 5 memory, CUDA 8. 0 • Intel E 5 -2650 processors running at 2. 6 GHZ and 16 GB DDR 3 , C++ STL on Ubuntu 14. 04 • Hardware 2 (new): • 2015 Nvidia GTX Titan X (Maxwell) GPU with 3, 072 CUDA cores and 12 GB GDDR 5 memory , CUDA 9. 1 • Intel Core i 7 -4770 running at 3. 4 GHZ and 32 GB DDR 3 memory, C++ STL on Ubuntu 16. 04

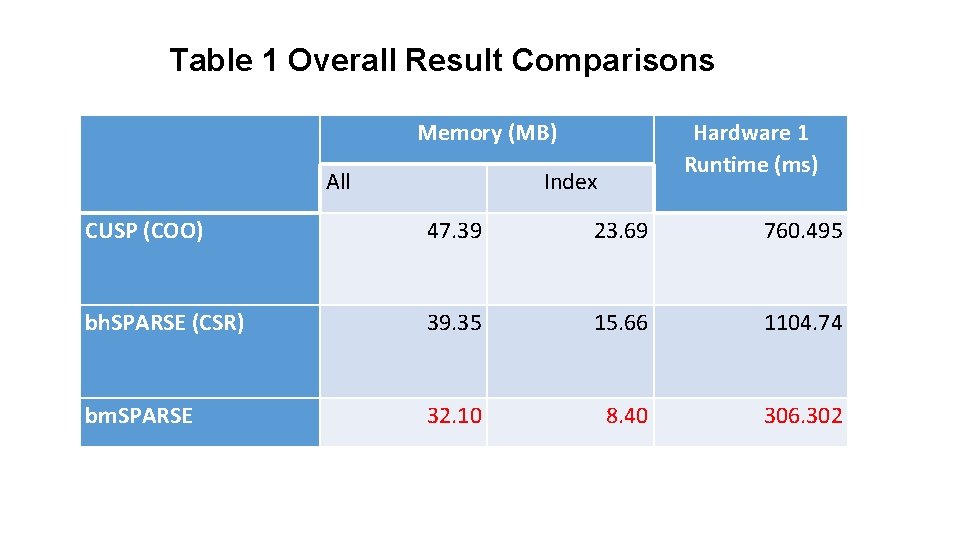
Table 1 Overall Result Comparisons Memory (MB) All Hardware 1 Runtime (ms) Index CUSP (COO) 47. 39 23. 69 760. 495 bh. SPARSE (CSR) 39. 35 15. 66 1104. 74 bm. SPARSE 32. 10 8. 40 306. 302

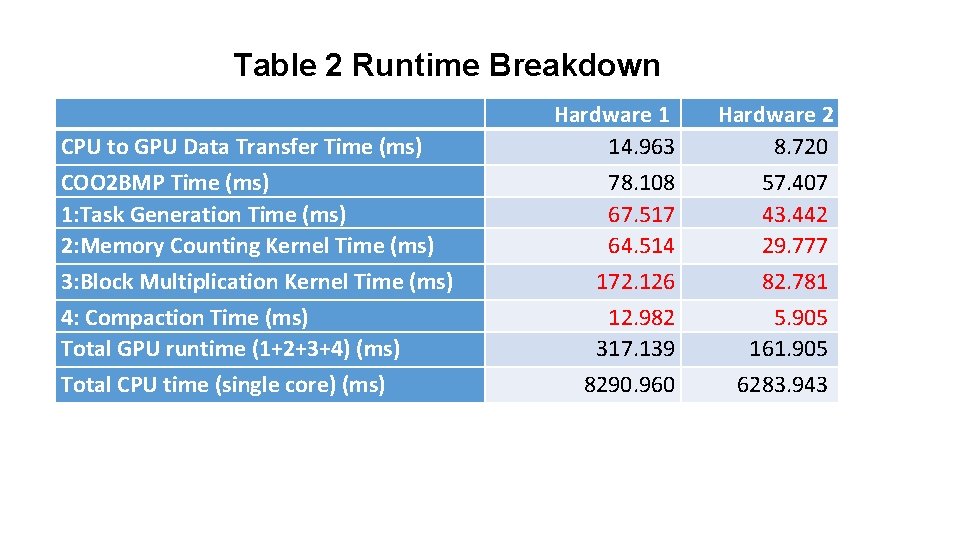
Table 2 Runtime Breakdown CPU to GPU Data Transfer Time (ms) COO 2 BMP Time (ms) 1: Task Generation Time (ms) 2: Memory Counting Kernel Time (ms) 3: Block Multiplication Kernel Time (ms) 4: Compaction Time (ms) Total GPU runtime (1+2+3+4) (ms) Total CPU time (single core) (ms) Hardware 1 14. 963 78. 108 67. 517 64. 514 172. 126 12. 982 317. 139 8290. 960 Hardware 2 8. 720 57. 407 43. 442 29. 777 82. 781 5. 905 161. 905 6283. 943

Conclusion & Discussions • The performance of bm. SPARSE is encouraging on the Web. Base 1 M dataset: 2. 4 X faster than CUSP and 3. 5 X faster than bh. SPARSE with significant memory footprint reduction • Preliminary experiments on additional sparse matrix datasets from UFL Sparse Matrix Collection have shown that bm. SPARSE technique does not always perform better than CUSP or b. HSPARSE. • This may indicate that our technique may be suitable to one or more specific categories of sparse matrices. • The performance on the Web. Base dataset suggests that graph data could be one of these categories although further investigations are needed

Future Work • • • Both graph and sparsity are ubiquitous, and are becoming increasingly important in both data management and machine learning (both are now mostly in-memory processing) Sp. GEMM is likely a key component in both forward and backward steps in gradient-based large-scale deep learning for both computation and memory efficiency (especially for fully-connected and convolutional layers) bm. SPARSE can be used as a building block for more efficient Deep Learning frameworks Next step: accelerating block level matrix multiplication on Volta Tensor cores (CUDA 9. 2) and integrating with Tensorflow (Next step): porting the task list generation implementation to Intel CPUs (multi-core and SIMD vectorization using TBB) and implementing block level matrix multiplication on Google TPUs (V 3) through Google Cloud