Regularization The problem of overfitting Machine Learning Size

Regularization The problem of overfitting Machine Learning

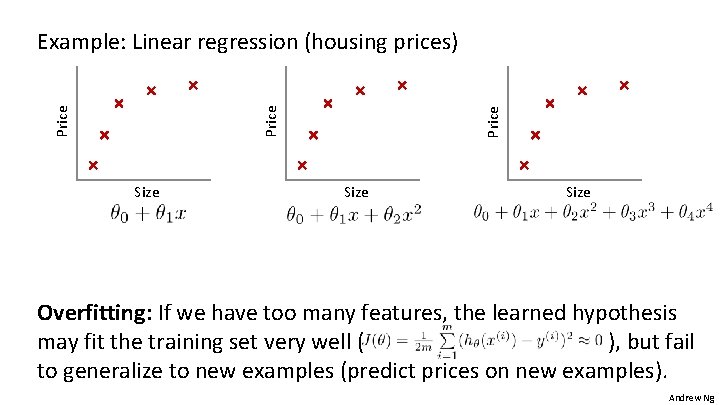
Size Price Example: Linear regression (housing prices) Size Overfitting: If we have too many features, the learned hypothesis may fit the training set very well ( ), but fail to generalize to new examples (predict prices on new examples). Andrew Ng

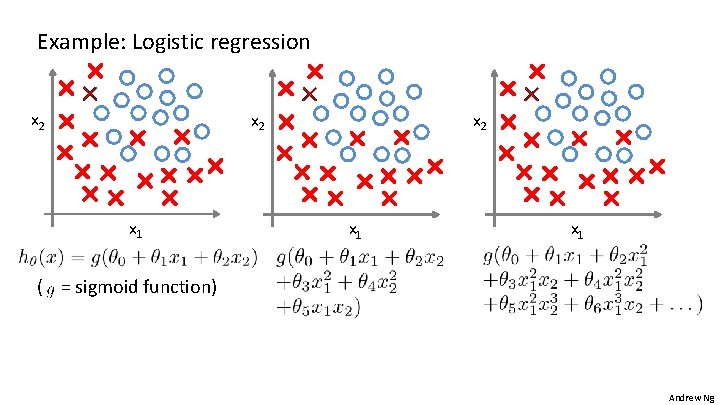
Example: Logistic regression x 2 x 2 x 1 x 1 ( = sigmoid function) Andrew Ng

size of house no. of bedrooms no. of floors age of house average income in neighborhood kitchen size Price Addressing overfitting: Size Andrew Ng

Addressing overfitting: Options: 1. Reduce number of features. ― Manually select which features to keep. ― Model selection algorithm (later in course). 2. Regularization. ― Keep all the features, but reduce magnitude/values of parameters. ― Works well when we have a lot of features, each of which contributes a bit to predicting. Andrew Ng

Regularization Cost function Machine Learning

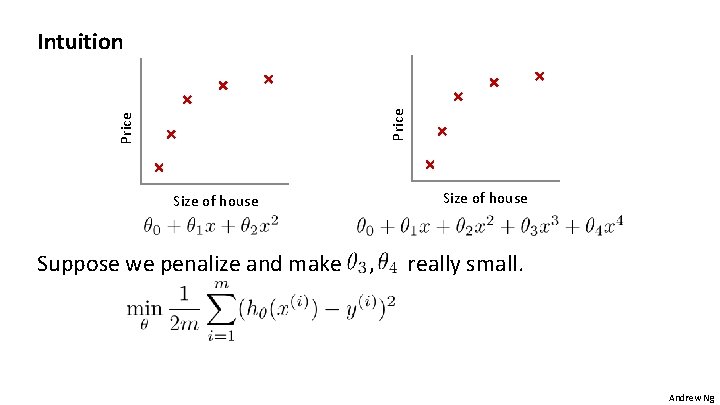
Price Intuition Size of house Suppose we penalize and make , really small. Andrew Ng

Regularization. Small values for parameters ― “Simpler” hypothesis ― Less prone to overfitting Housing: ― Features: ― Parameters: Andrew Ng

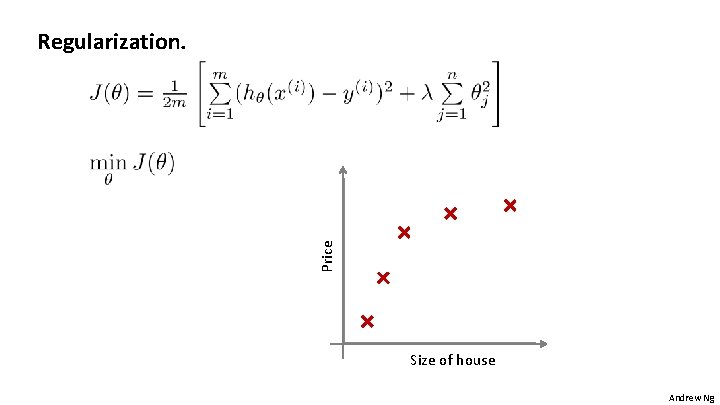
Price Regularization. Size of house Andrew Ng

In regularized linear regression, we choose to minimize Price What if is set to an extremely large value (perhaps for too large for our problem, say )? Size of house Andrew Ng

Regularization Regularized linear regression Machine Learning

Regularized linear regression

Gradient descent Repeat Andrew Ng

Regularization Regularized logistic regression Machine Learning

Regularized logistic regression. x 2 x 1 Cost function: Andrew Ng

Gradient descent Repeat Andrew Ng

Advanced optimization function [j. Val, gradient] = cost. Function(theta) j. Val = [ code to compute ]; gradient(1) = [code to compute ]; gradient(2) = [code to compute ]; gradient(3) = [code to compute ]; gradient(n+1) = [ code to compute ]; Andrew Ng