Regular Languages Closure Properties Take 1 CS 154

Regular Languages’ Closure Properties, Take 1 CS 154, Omer Reingold

Closure Properties for Regular Languages Union: A B = { w | w A or w B } Intersection: A B = { w | w A and w B } Complement: A = { w Σ* | w A } Reverse: AR = { w 1 …wk | wk …w 1 A, wi Σ} Concatenation: A B = { vw | v A and w B } Star: A* = { s 1 … sk | k ≥ 0 and each si A } Theorem: if A and B are regular then so are: A B, A, AR , A B, and A*

Union Theorem for Regular Languages Given two languages L 1 and L 2 recall that the union of L 1 and L 2 is L 1 L 2 = { w | w L 1 or w L 2 } Theorem: The union of two regular languages is also a regular language

Theorem: The union of two regular languages is also a regular language Proof: Let 1 M 1 = (Q 1, Σ, 1, q 0, F 1) be a finite automaton for L 1 and 2 M 2 = (Q 2, Σ, 2, q 0, F 2) be a finite automaton for L 2

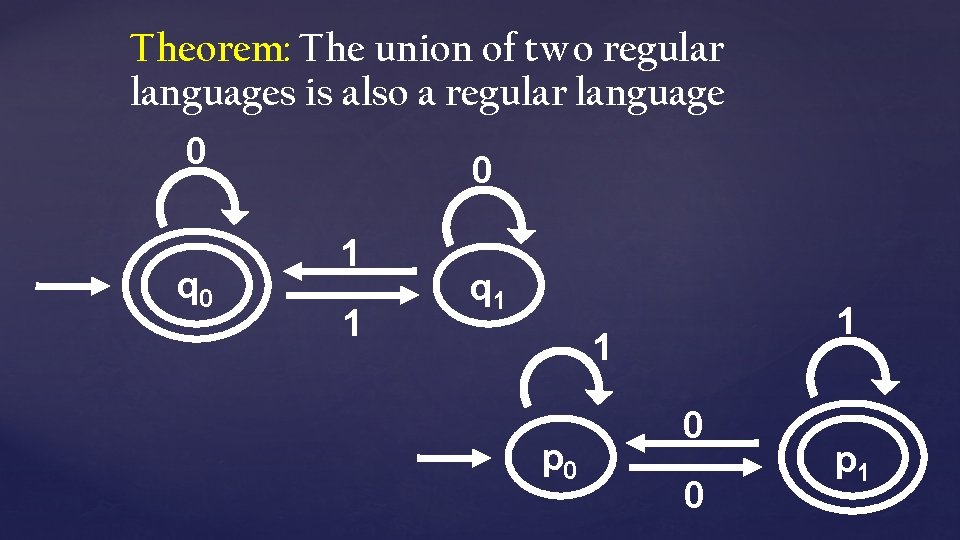
Proof Idea: Run both M 1 and M 2 “in parallel”! 1 M 1 = (Q 1, Σ, 1, q 0, F 1) recognizes L 1 and 2 M 2 = (Q 2, Σ, 2, q 0, F 2) recognizes L 2 Q = pairs of states, one from M 1 and one from M 2 = { (q 1, q 2) | q 1 Q 1 and q 2 Q 2 } = Q 1 Q 2 q 0 = (q 01, q 02) F = { (q 1, q 2) | q 1 F 1 OR q 2 F 2 } ( (q 1, q 2), ) = ( 1(q 1, ), 2(q 2, ))

Theorem: The union of two regular languages is also a regular language 0 q 0 0 1 1 q 1 1 1 p 0 0 0 p 1

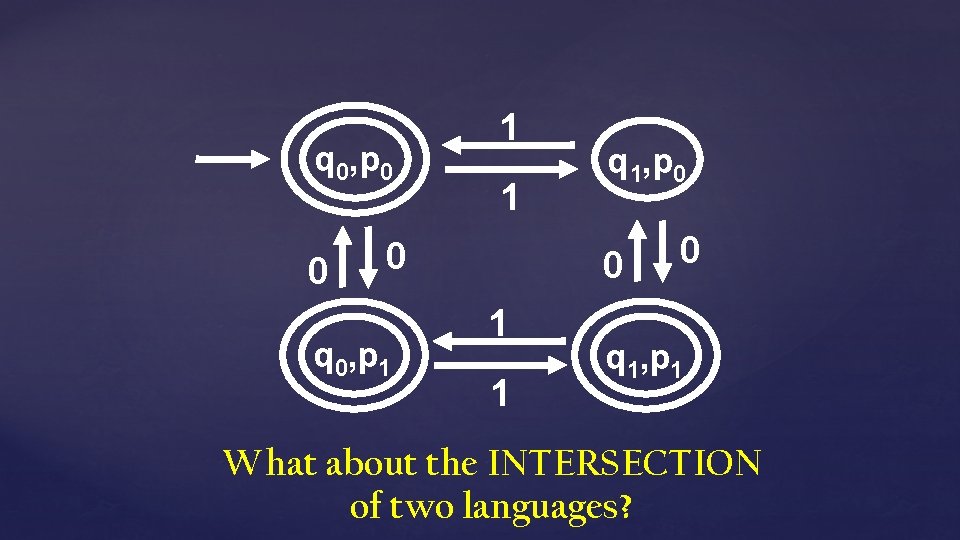
q 0, p 0 0 1 1 0 q 0, p 1 q 1, p 0 0 1 1 0 q 1, p 1 What about the INTERSECTION of two languages?

Proof Idea: Run both M 1 and M 2 “in parallel”! 1 M 1 = (Q 1, Σ, 1, q 0, F 1) recognizes L 1 and 2 M 2 = (Q 2, Σ, 2, q 0, F 2) recognizes L 2 Q = pairs of states, one from M 1 and one from M 2 = { (q 1, q 2) | q 1 Q 1 and q 2 Q 2 } = Q 1 Q 2 q 0 = (q 01, q 02) F = { (q 1, q 2) | q 1 F 1 AND q 2 F 2 } ( (q 1, q 2), ) = ( 1(q 1, ), 2(q 2, ))

Union Theorem for Regular Languages: The union of two regular languages is also a regular language “Regular Languages Are Closed Under Union” Intersection Theorem for Regular Languages: The intersection of two regular languages is also a regular language “Regular Languages Are Closed Under Intersextion”

Complement Theorem for Regular Languages The complement of a regular language is also a regular language: If L is regular than so is L= { w Σ* | w L } Proof ?

Closure Properties for Regular Languages Union: A B = { w | w A or w B } Intersection: A B = { w | w A and w B } Complement: A = { w Σ* | w A } Reverse: AR = { w 1 …wk | wk …w 1 A, wi Σ} Concatenation: A B = { vw | v A and w B } Star: A* = { s 1 … sk | k ≥ 0 and each si A } Theorem: if A and B are regular then so are: A B, A, AR , A B, and A*

The Reverse of a Language Reverse of L: LR = { w 1 …wk | wk …w 1 L, wi Σ} Theorem: If L is regular, then is LR also regular If L is recognized by the usual kind of DFA, Then LR is recognized by a DFA that reads its strings from right to left How can every “Right-to-Left” DFA be replaced by a normal “Left-to-Right” DFA?

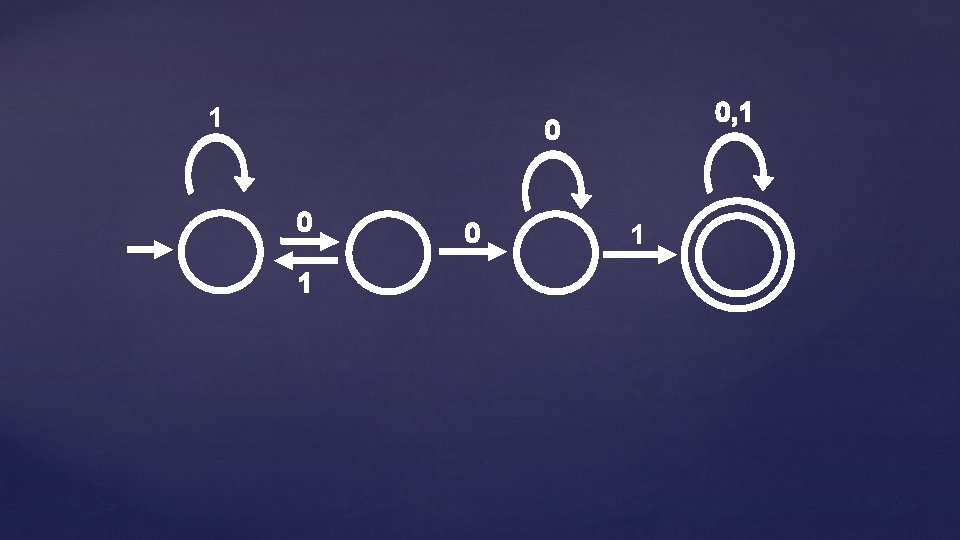
Reversing DFAs Assume L is a regular language. Let M be a DFA that recognizes L We want to build a machine MR that accepts LR If M accepts w, then w describes a directed path in M from the start state to an accept state First Attempt: Try to define MR as M with the arrows reversed, turn start state into a final state, turn final states into starts

Problem: MR is not always a DFA! It could have many start states Some states may have more than one outgoing edge, or none at all!

1 0, 1 0 0 1

Non-deterministic Finite Automata (NFA) 1 0, 1 0 0 0 1 1 What happens with 100? We will say this new machine accepts a string if there is some path that reaches some accept state from some start state