Regular Expressions Highlights A regular expression is used

Regular Expressions • Highlights: – – A regular expression is used to specify a language, and it does so precisely. Regular expressions are very intuitive. Regular expressions are very useful in a variety of contexts. Given a regular expression, an NFA-ε can be constructed from it automatically. – Thus, so can an NFA be constructed, and a DFA, and a corresponding program, all automatically! 1

Two Operations • Concatenation: – – – • Language Concatenation: L 1 L 2 = {xy | x is in L 1 and y is in L 2} – – – • x = 010 y = 1101 xy = 010 1101 L 1 = {01, 00} L 2 = {11, 010} L 1 L 2 = {01 11, 01 010, 00 11, 00 010} Language Union: – – L 1 = {01, 00} L 2 = {01, 11, 010} – L 1 UL 2 = {01, 00, 11, 010} 2

Operations on Languages • Let L, L 1, L 2 be subsets of Σ* • Concatenation: L 1 L 2 = {xy | x is in L 1 and y is in L 2} • Concatenating a language with itself: L 0 = {ε} Li = LLi-1, for all i >= 1 3

Kleene closure Say, L, or L 1 ={a, abc, ba}, on Σ ={a, b, c} Then, L 2 = {aa, aabc, aba, abcabc, abcba, baabc, baba} L 3= {a, abc, ba}. L 2 …. . But, L 0 = {ε} Kleene closure of L, L* = {ε, L 1, L 2, L 3, . . . } 4

Operations on Languages • Let L, L 1, L 2 be subsets of Σ* • Concatenation: L 1 L 2 = {xy | x is in L 1 and y is in L 2} • Union is set union of L 1 and L 2 • Kleene Closure: L* = Li = L 0 U L 1 U L 2 U… • Positive Closure: L+ = Li = L 1 U L 2 U… • Question: Does L+ contain ε? 5

Definition of a Regular Expression • Let Σ be an alphabet. The regular expressions over Σ are: – Ø – ε – a Represents the empty set { } Represents the set {ε} Represents the set {a}, one string of length 1, for any symbol a in Σ Let r and s be regular expressions that represent the sets R and S, respectively. – – • r+s rs r* (r) Represents the set R U S Represents the set R* Represents the set R (precedence 3) (precedence level 2) (highest precedence, level 1) (not an operator, rather provides precedence) If r is a regular expression, then L(r) is used to denote the corresponding language. 6

• Examples: Let Σ = {0, 1} (0 + 1)* 01* All strings of 0’s and 1’s 0 followed by any number 1’s 0(0 + 1)* All strings of 0’s and 1’s, beginning with a 0 (0 + 1)*1 All strings of 0’s and 1’s, ending with a 1 (0 + 1)*0(0 + 1)* All strings of 0’s and 1’s containing at least one 0 (0 + 1)*0(0 + 1)* All strings of 0’s and 1’s containing at least two 0’s (0 + 1)*01*01* All strings of 0’s and 1’s containing at least two 0’s (1 + 01*0)* All strings of 0’s and 1’s containing an even number of 0’s 1*(01*01*)* All strings of 0’s and 1’s containing an even number of 0’s (1*01*0)*1* (0+1)* = (0*1*)* All strings of 0’s and 1’s containing an even number of 0’s Any string, or (sigma)*, sigma={0, 1} in all cases here 7 • Question: Is there a unique minimum regular expression for a given language?

• Identities: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 1. Øu = uØ = Ø Like multiplying by 0 εu = uε = u Like multiplying by 1 Ø* = ε L* = Li = L 0 U L 1 U L 2 U… ε* = ε = { ε} u+v = v+u u+Ø=u u+u=u u* = (u*)* u(v+w) = uv+uw [which operation is hidden before parenthesis? ] (u+v)w = uw+vw (uv)*u = u(vu)* [note: you have to have a single u, at start or end] [note (uv)* =/= u*v*] (u+v)* = (u*+v)* = u*(u+v)* = (u+vu*)* = (u*v*)* = u*(vu*)* = (u*v)*u* 8

Equivalence of Regular Expressions and NFA-εs • Note: Throughout the following, keep in mind that a string is accepted by an NFA-ε if there exists ANY path from the start state to any final state. • Lemma 1: Let r be a regular expression. Then there exists an NFA-ε M such that L(M) = L(r). Furthermore, M has exactly one final state with no transitions out of it. • Proof: (by induction on the number of operators, denoted by OP(r), in r). 9

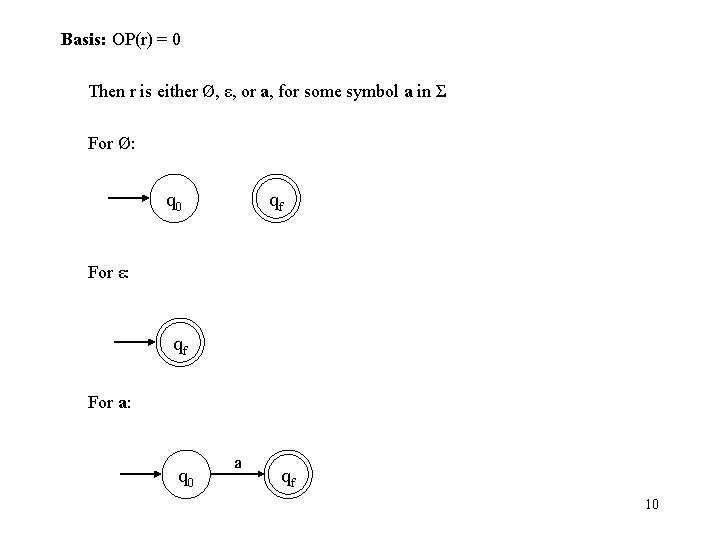
Basis: OP(r) = 0 Then r is either Ø, ε, or a, for some symbol a in Σ For Ø: q 0 qf For ε: qf For a: q 0 a qf 10

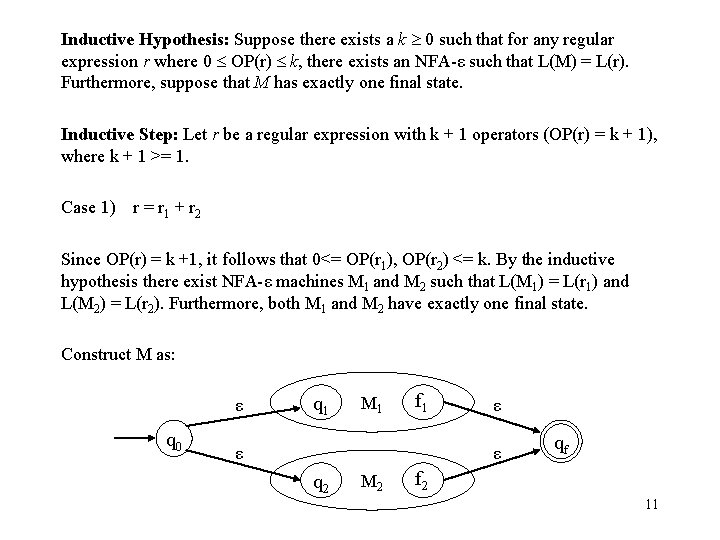
Inductive Hypothesis: Suppose there exists a k 0 such that for any regular expression r where 0 OP(r) k, there exists an NFA-ε such that L(M) = L(r). Furthermore, suppose that M has exactly one final state. Inductive Step: Let r be a regular expression with k + 1 operators (OP(r) = k + 1), where k + 1 >= 1. Case 1) r = r 1 + r 2 Since OP(r) = k +1, it follows that 0<= OP(r 1), OP(r 2) <= k. By the inductive hypothesis there exist NFA-ε machines M 1 and M 2 such that L(M 1) = L(r 1) and L(M 2) = L(r 2). Furthermore, both M 1 and M 2 have exactly one final state. Construct M as: ε q 0 q 1 M 1 f 1 ε ε ε q 2 M 2 qf f 2 11

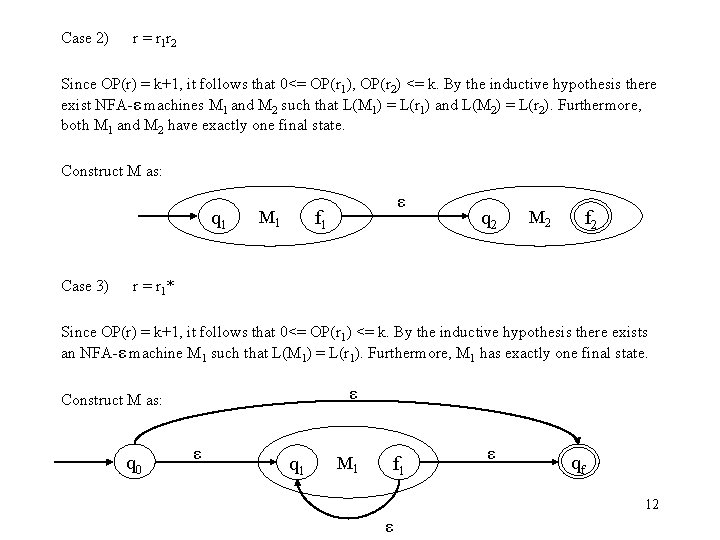
Case 2) r = r 1 r 2 Since OP(r) = k+1, it follows that 0<= OP(r 1), OP(r 2) <= k. By the inductive hypothesis there exist NFA-ε machines M 1 and M 2 such that L(M 1) = L(r 1) and L(M 2) = L(r 2). Furthermore, both M 1 and M 2 have exactly one final state. Construct M as: q 1 Case 3) ε f 1 M 1 q 2 M 2 f 2 r = r 1* Since OP(r) = k+1, it follows that 0<= OP(r 1) <= k. By the inductive hypothesis there exists an NFA-ε machine M 1 such that L(M 1) = L(r 1). Furthermore, M 1 has exactly one final state. ε Construct M as: q 0 ε q 1 M 1 f 1 ε qf 12 ε

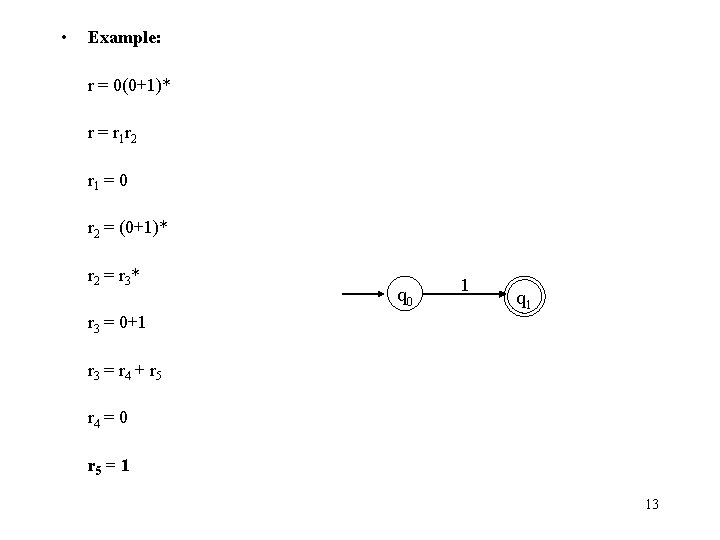
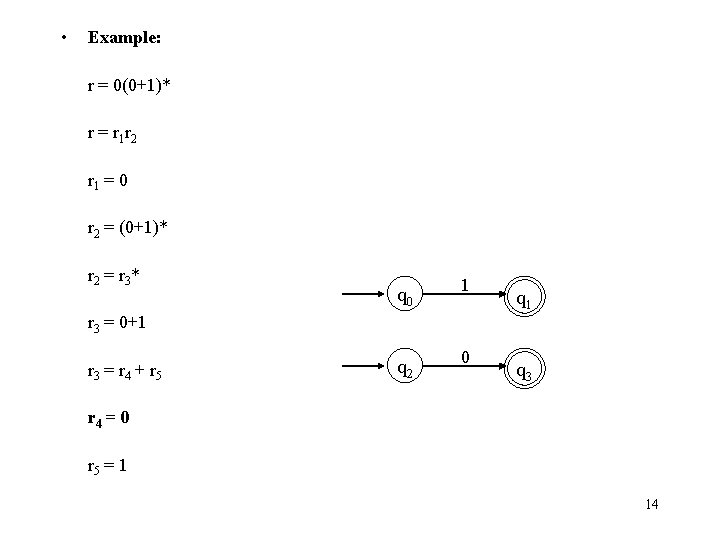
• Example: r = 0(0+1)* r = r 1 r 2 r 1 = 0 r 2 = (0+1)* r 2 = r 3 * q 0 1 q 1 r 3 = 0+1 r 3 = r 4 + r 5 r 4 = 0 r 5 = 1 13

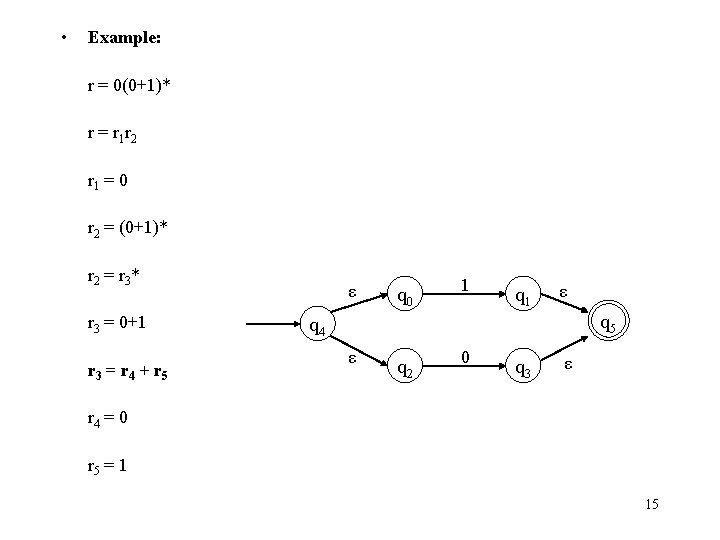
• Example: r = 0(0+1)* r = r 1 r 2 r 1 = 0 r 2 = (0+1)* r 2 = r 3 * q 0 1 q 2 0 q 1 r 3 = 0+1 r 3 = r 4 + r 5 q 3 r 4 = 0 r 5 = 1 14

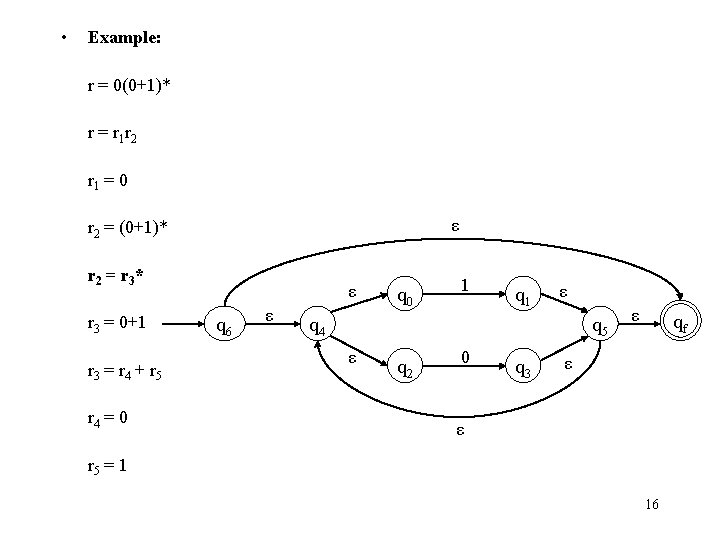
• Example: r = 0(0+1)* r = r 1 r 2 r 1 = 0 r 2 = (0+1)* r 2 = r 3 * r 3 = 0+1 r 3 = r 4 + r 5 ε q 0 1 q 1 ε q 5 q 4 ε q 2 0 q 3 ε r 4 = 0 r 5 = 1 15

• Example: r = 0(0+1)* r = r 1 r 2 r 1 = 0 ε r 2 = (0+1)* r 2 = r 3 * r 3 = 0+1 r 3 = r 4 + r 5 r 4 = 0 ε q 6 ε q 0 1 q 1 ε q 4 q 5 ε q 2 0 q 3 ε qf ε ε r 5 = 1 16

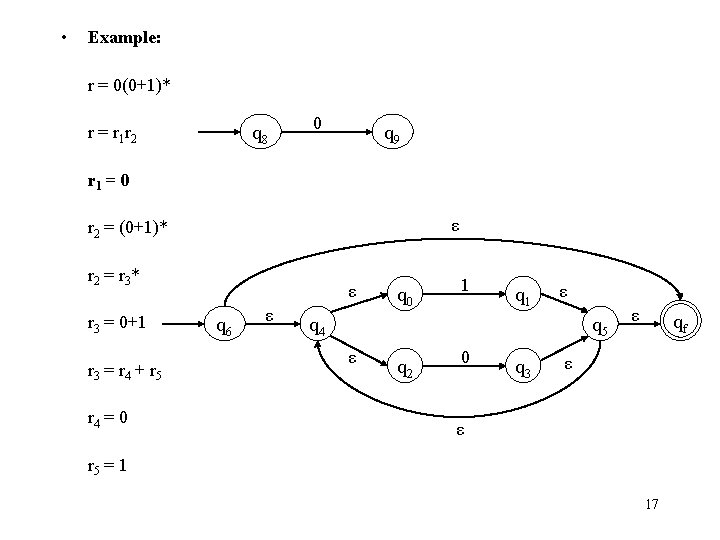
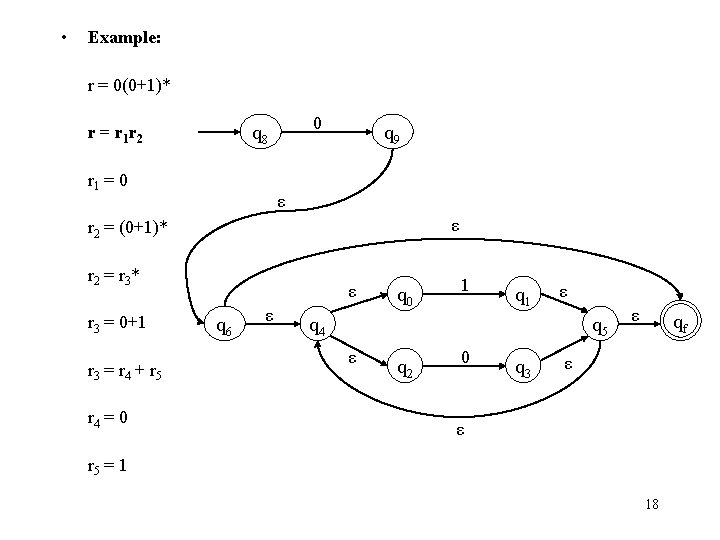
• Example: r = 0(0+1)* q 8 r = r 1 r 2 0 q 9 r 1 = 0 ε r 2 = (0+1)* r 2 = r 3 * r 3 = 0+1 r 3 = r 4 + r 5 r 4 = 0 ε q 6 ε q 0 1 q 1 ε q 4 q 5 ε q 2 0 q 3 ε qf ε ε r 5 = 1 17

• Example: r = 0(0+1)* 0 q 8 r = r 1 r 2 r 1 = 0 q 9 ε ε r 2 = (0+1)* r 2 = r 3 * r 3 = 0+1 r 3 = r 4 + r 5 r 4 = 0 ε q 6 ε q 0 1 q 1 ε q 4 q 5 ε q 2 0 q 3 ε qf ε ε r 5 = 1 18

Equivalence Proved So Far • DFA ≡ NFA-e • • Every regular expression has an NFA-e, so, r. e subset-equal NFA-e • • We did not show to convert an NFA-e to its r. e, so, The equivalence of r. e. to the machines is not show yet. • • We know at this stage, r. e. is subset-equal regular language, but Not other way round • Will show now, how to convert DFA to its accepted r. e. 19

Definitions Required to Convert a DFA to a Regular Expression • Let M = (Q, Σ, δ, q 1, F) be a DFA with state set Q = {q 1, q 2, …, qn}, and define: Ri, j = { x | x is in Σ* and δ(qi, x) = qj} Ri, j is the set of all strings that define a path in M from qi to qj. • Note that states have been numbered starting at q 1, not q 0! 20

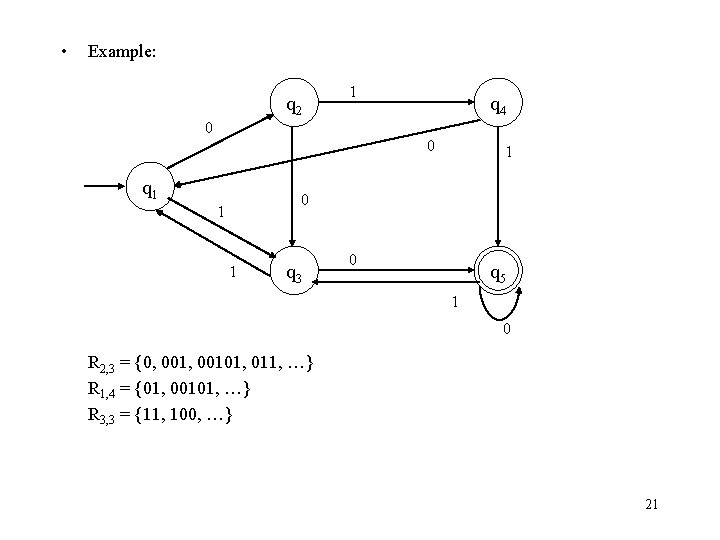
• Example: q 2 1 q 4 0 0 q 1 1 0 1 1 q 3 0 q 5 1 0 R 2, 3 = {0, 00101, 011, …} R 1, 4 = {01, 00101, …} R 3, 3 = {11, 100, …} 21

• In words: Rki, j is the set of all the strings that define a path in M from qi to qj but that passes through no state numbered greater than k. • Definition: Rki, j = { x | x is in Σ* and δ(qi, x) = qj, and for no u where 1 |u| < |x| and x = uv there is no case such that δ(qi, u) = qp where p>k} • Note that it may be true that i>=k or j>=k, only the intermediate states on the path from i to j may not be >k. 22

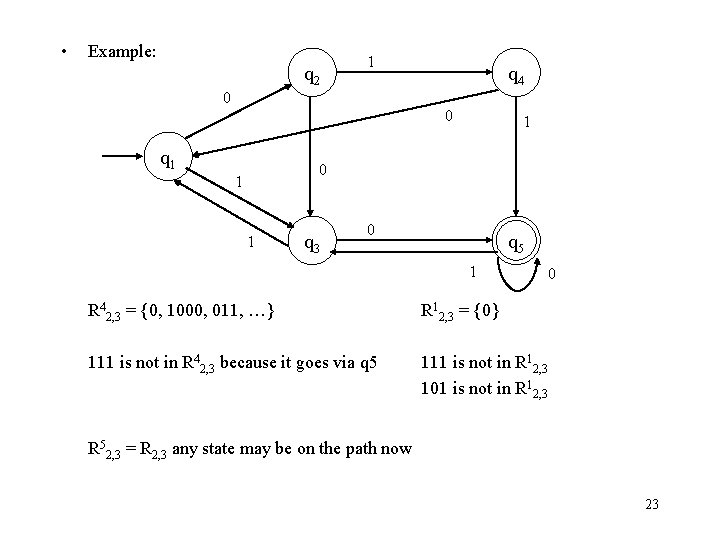
• Example: q 2 1 q 4 0 0 q 1 1 0 1 1 q 3 0 q 5 1 0 R 42, 3 = {0, 1000, 011, …} R 12, 3 = {0} 111 is not in R 42, 3 because it goes via q 5 111 is not in R 12, 3 101 is not in R 12, 3 R 52, 3 = R 2, 3 any state may be on the path now 23

• Obeservations: 1) Rni, j = Ri, j , where n is the number of states 2) Rk-1 i, j is a subset of Rki, j 3) L(M) = Rn 1, q = R 1, q 4) R 0 i, j = Easily computed from the DFA! 5) Rki, j = Rk-1 i, k (Rk-1 k, k)* Rk-1 k, j U Rk-1 i, j Now, you see the purpose of introducing k: So that we can write it as a RE 24

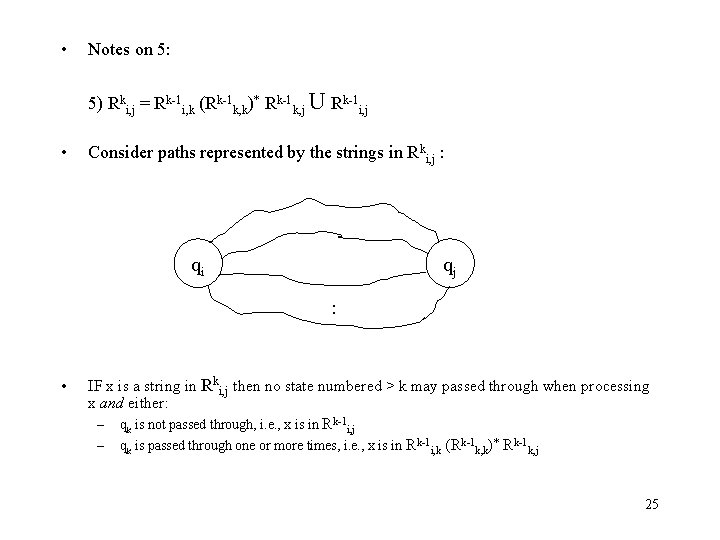
• Notes on 5: 5) Rki, j = Rk-1 i, k (Rk-1 k, k)* Rk-1 k, j U Rk-1 i, j • Consider paths represented by the strings in Rki, j : qi qj : • IF x is a string in Rki, j then no state numbered > k may passed through when processing x and either: – qk is not passed through, i. e. , x is in Rk-1 i, j – qk is passed through one or more times, i. e. , x is in Rk-1 i, k (Rk-1 k, k)* Rk-1 k, j 25

• Lemma 2: Let M = (Q, Σ, δ, q 1, F) be a DFA. Then there exists a regular expression r such that L(M) = L(r). • Proof: First we will show (by induction on k) that for all i, j, and k, where 1 i, j n and 0 k n, that there exists a regular expression r such that L(r) = Rki, j. Basis: k=0 R 0 i, j contains single symbols, one for each transition from qi to qj, and possibly ε if i=j. case 1) No transitions from qi to qj and i != j r 0 i, j = Ø case 2) At least one (m 1) transition from qi to qj and i != j r 0 i, j = a 1 + a 2 + a 3 + … + am where δ(qi, ap) = qj, for all 1 p m 26

case 3) No transitions from qi to qj and i = j r 0 i, j = ε case 4) At least one (m 1) transition from qi to qj and i = j r 0 i, j = a 1 + a 2 + a 3 + … + am + ε where δ(qi, ap) = qj for all 1 p m Inductive Hypothesis: Suppose that Rk-1 i, j can be represented by the regular expression rk-1 i, j for all 1 i, j n, and some k 1. Inductive Step: Consider Rki, j = Rk-1 i, k (Rk-1 k, k)* Rk-1 k, j U Rk-1 i, j. By the inductive hypothesis there exist regular expressions rk-1 i, k , rk-1 k, j , and rk-1 i, j generating Rk-1 i, k , Rk-1 k, j , and Rk-1 i, j , respectively. Thus, if we let rki, j = rk-1 i, k (rk-1 k, k)* rk-1 k, j + rk-1 i, j then rki, j is a regular expression generating Rki, j , i. e. , L(rki, j) = Rki, j. 27

• Finally, if F = {qj 1, qj 2, …, qjr}, then rn 1, j 1 + rn 1, j 2 + … + rn 1, jr is a regular expression generating L(M). • Note: not only does this prove that the regular expressions generate the regular languages, but it also provides an algorithm for computing it! 28

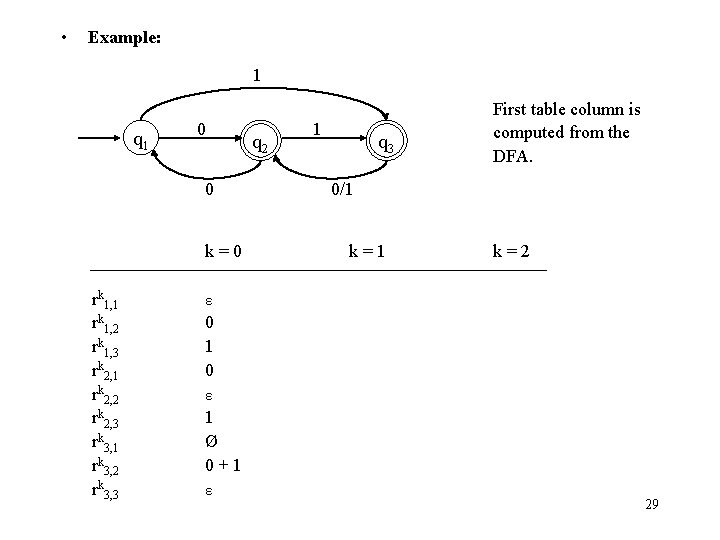
• Example: 1 q 1 0 0 k=0 rk 1, 1 rk 1, 2 rk 1, 3 rk 2, 1 rk 2, 2 rk 2, 3 rk 3, 1 rk 3, 2 rk 3, 3 q 2 1 q 3 First table column is computed from the DFA. 0/1 k=2 ε 0 1 0 ε 1 Ø 0+1 ε 29

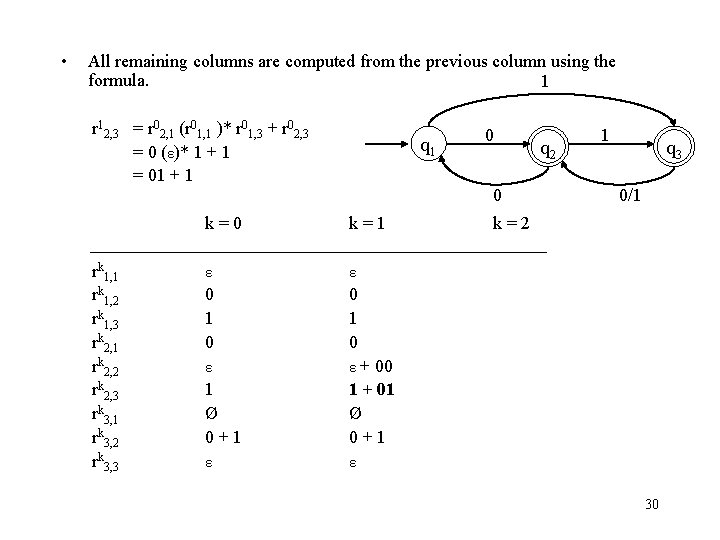
• All remaining columns are computed from the previous column using the formula. 1 r 12, 3 = r 02, 1 (r 01, 1 )* r 01, 3 + r 02, 3 = 0 (ε)* 1 + 1 = 01 + 1 rk 1, 2 rk 1, 3 rk 2, 1 rk 2, 2 rk 2, 3 rk 3, 1 rk 3, 2 rk 3, 3 q 1 0 0 k=1 ε ε 0 1 0 ε ε + 00 1 Ø 0+1 1 + 01 Ø 0+1 ε ε q 2 1 q 3 0/1 k=2 30

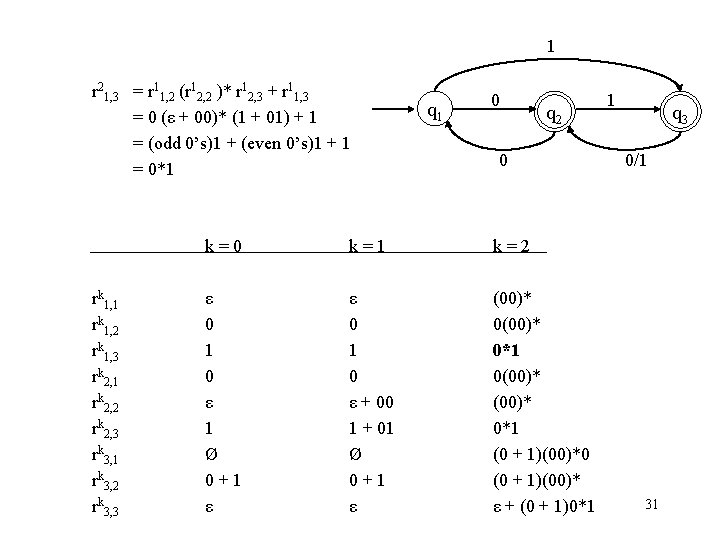
1 r 21, 3 = r 11, 2 (r 12, 2 )* r 12, 3 + r 11, 3 = 0 (ε + 00)* (1 + 01) + 1 = (odd 0’s)1 + (even 0’s)1 + 1 = 0*1 rk 1, 2 rk 1, 3 rk 2, 1 rk 2, 2 rk 2, 3 rk 3, 1 rk 3, 2 rk 3, 3 q 1 0 q 2 0 k=1 k=2 ε 0 1 0 ε 1 Ø 0+1 ε ε 0 1 0 ε + 00 1 + 01 Ø 0+1 ε (00)* 0*1 0(00)* 0*1 (0 + 1)(00)*0 (0 + 1)(00)* ε + (0 + 1)0*1 1 q 3 0/1 31

• To complete the regular expression for the language, we compute: r 31, 2 + r 31, 3 [complete this] rk 1, 1 rk 1, 2 rk 1, 3 rk 2, 1 rk 2, 2 rk 2, 3 rk 3, 1 rk 3, 2 rk 3, 3 k=0 k=1 k=2 k=3 ε 0 1 0 ε 1 Ø 0+1 ε ε 0 1 0 ε + 00 1 + 01 Ø 0+1 ε (00)* 0*1 0(00)* 0*1 (0 + 1)(00)*0 (0 + 1)(00)* ε + (0 + 1)0*1 32

Now we have proved equivalence of all • DFA ≡ NFA-e • DFA can be converted to its r. e. , or DFA subset-equal r. e. • R. e. subset-equal NFA-e • So, r. e ≡ NFA-e, or • • DFA ≡ NFA-e ≡ r. e. (note my abuse of concepts, r. e. is about language) • We proved, r. e. expresses regular language, and only regular language 33

• Theorem: Let L be a language. Then there exists an a regular expression r such that L = L(r) if and only if there exits a DFA M such that L = L(M). • Proof: (if) Suppose there exists a DFA M such that L = L(M). Then by Lemma 2 there exists a regular expression r such that L = L(r). (only if) Suppose there exists a regular expression r such that L = L(r). Then by Lemma 1 there exists a DFA M such that L = L(M). • Corollary: The regular expressions define the regular languages. • Note: The conversion from a regular expression to a DFA and a program accepting L(r) is now complete, and fully automated! 34