Regular Expressions CIS 361 Fundamental Problems n Need

Regular Expressions CIS 361

Fundamental Problems n Need finite descriptions of infinite sets of strings. n n Discover and specify “regularity”. The set of languages over a finite alphabet is uncountable, while the set of descriptions is countable

Regular Expressions n Language L is regular if there exists a finite acceptor for it n Any language that is described by a regular expression can be accepted by some finite automaton

Regular Expressions n Regular expressions n Combination of strings of symbols from some alphabet, parentheses and operators U, . , * n n n U is union (some literature uses +). (or nothing) is concatenation * is star closure or Kleene star n n n superscripted repetition, 0 or more times + is closure n n superscripted repetition, 1 or more times

Specifying Lexical Structure Using Regular Expressions n n Have some alphabet = set of symbols Regular expressions are built from: n n n - empty string Any letter from r 1 r 2 – String r 1 followed by r 2 (concatenation) r 1 U r 2 (r 1 + r 2) – either regular expression r 1 or r 2 (union) r* - iterated sequence and choice | r r | … Parentheses to indicate grouping/precedence

Regular Expressions n Operations n n n Union Complement Intersection Difference Concatenation Repetition n n Kleene star Plus operator

Regular Expressions n Union n L M The union of two regular expressions Q and R is Q U R In terms of automata A and B, respectively n n create a new initial state q connect it to the initial states of A and B by transitions

Regular Expressions n Complement n n * - L To construct the complement of a regular expression L, inspect the automaton that accepts its strings n n n convert the automaton for L to a deterministic automaton flips favorable and nonfavorable states construct a regular expression for strings accepted by the updated automaton

Regular Expressions n n Complement of bit strings with at least one “ 1” = bit strings containing no “ 1”s = 0* Complement of bit strings with exactly one “ 1” = bit strings containing no “ 1”s U bit strings with at least two “ 1”s = 0* U (0* 1 0*)(0 U 1)*

Regular Expressions n Intersection n n L M Apply De. Morgan’s law n Union of the complements of L and M

Regular Expressions n Difference n n L–M Can be expressed as the intersection of languages L and * - M

Regular Expressions n Concatenation n n Strings u and v over alphabet is string uv Languages L 1 and L 2 concatenated n n L 1 L 2 ={uv|u L 1, v L 2} Can be extended to any finite number of languages

Regular Expressions n Concatenation n n LM Algorithm connects every favorable state of L to the initial state of M by an arrow labeled n n Favorable states of L become non-favorable Favorable states of M become favorable states of the new automaton

Regular Expressions n Kleene star n n L* In terms of automaton n n connect every favorable state of L to the initial state of L by a transition labeled create a new initial state s, make it the only favorable state and connect it to the old initial state by transition

Regular Expressions n Plus (+) L+ n In terms of automaton n n connect every favorable state of L to the initial state of L by a transition labeled n That’s it. This gets one or more times to a favorable state

Naming Languages Regular sets can be named using the derivation in terms of the seed elements and the closure operations. Regular expressions formalize this approach. Regular sets Regular Expressions Numbers Numerals Semantics Syntax n

Example n Regular expressions for strings over {a, b} containing at least one “a”. n Focus on the one “a” (a u b)*a(a u b)* n Focus on the leftmost “a” b*a(a u b)* n Focus on the “a”s b*ab*(ab*)* n Further optimization b*(ab*)+

Equivalence of regular expressions Two regular expressions are equivalent if they represent the same regular set.

Concept of Language Generated by Regular Expressions n n n Set of all strings generated by a regular expression is the language of the regular expression In general, a language may be (countably) infinite A string in a language is often called a token

Examples of Languages and Regular Expressions n n = { 0, 1, . } n (0 U 1)* - Binary floating point numbers n (00)* - even-length all-zero strings n 1*(01*01*)* - strings with even number of zeros = {A, …, Z, a, …, z, 0, …, 9, _ } * identifiers n (A U … U z)(A U … U z U 0 U … U 9 U _) * n (1 U … U 9)(0 U … U 9) natural numbers (no negatives) n (0|1|2)* - trinary (base 3) numbers

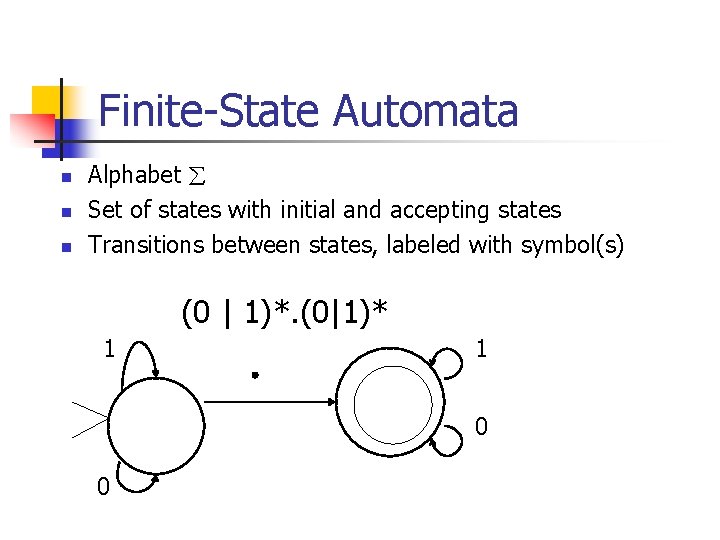
Finite-State Automata n n n Alphabet Set of states with initial and accepting states Transitions between states, labeled with symbol(s) (0 | 1)*. (0|1)* 1 1 0 0