Regular expressions and automata Introduction Finite State Automaton

Regular expressions and automata Introduction Finite State Automaton (FSA) Finite State Transducers (FST) NLP FS Models

Regular expressions Standard notation for characterizing text sequences Specifying text strings: Web search: woodchuck (with an optional final s) (lower/upper case) Computation of frequencies Word-processing (Word, emacs, Perl) NLP FS Models

Regular expressions and automata Regular expressions can be implemented by the finite-state automaton. Finite State Automaton (FSA) a significant tool of computational lingusitics. Variations: - Finite State Transducers (FST) - N-gram - Hidden Markov Models NLP FS Models

Aplications: Increasing use in NLP Morphology Phonology Lexical generation ASR POS tagging simplification of CFG Information Extraction NLP FS Models

Regular expressions (REs) A RE formula in a special language (an algebraic notation) to specify simple classes of strings: a sequence of symbols (i. e, alphanumeric characters). woodchucks, a, song, !, Mary says REs are used to – Specify search strings - to define a pattern to search through a corpus – Define a language NLP FS Models

Regular expressions (REs) - Case sensitive: woodchucks different from Woodchucks - [] means disjuntion [Ww]oodchucks [1234567890] (any digit) [A-Z] an uppercase letter - [^] means cannot be [^A-Z] not an uppercase letter [^Ss] neither 'S' nor 's' NLP FS Models

Regular expressions - ? means preceding character or nothing Woodchucks? means Woodchucks or Woodchuck colou? r color or colour - * (kleene star)- zero or more occurrences of the immediately previous character a* any string or zero or more as (a, aa, hello) [0 -9]* - any integer - + one or more occurrences [0 -9]+ NLP FS Models

Regular expressions - Disjunction operator | cat|dog - There are other more complex operators - Operator precedence hierarchy - Very useful in substitutions (i. e. Dialogue) NLP FS Models

Regular expressions - Examples of substitutions in dialogue User: Men are all alike ELIZA: IN WHAT WAY s/. *all. */ IN WHAT WAY User: They're always bugging us about something ELIZA: CAN YOU TINK OF A SPECIFIC EXAMPLE s/*always. */ CAN YOU TINK OF A SPECIFIC EXAMPLE NLP FS Models

• Why? • Temporal and spatial efficiency • Some FS Machines can be determined and optimized for leading to more compact representations • Possibility to be used in cascade form NLP FS Models

Some readings Kenneth R. Beesley and Lauri Karttunen, Finite State Morphology, CSLI Publications, 2003 Roche and Schabes 1997 Finite-State Language Processing. 1997. MIT Press, Cambridge, Massachusetts. References to Finite-State Methods in Natural Language Processing http: //www. cis. upenn. edu/~cis 639/docs/fsrefs. html NLP FS Models

Some toolbox ATT FSM tools http: //www 2. research. att. com/~fsmtools/fsm/ Beesley, Kartunnen book http: //www. stanford. edu/~laurik/fsmbook/hom e. html Carmel http: //www. isi. edu/licensed-sw/carmel/ Dan Colish's Py. FSA (Python FSA) https: //github. com/dcolish/Py. FSA NLP FS Models

Equivalence Regular Expressions Regular Languages FSA NLP FS Models

Regular Expressions • • Basically they are combinations of simple units (character or strings) with connectives as concatenation, disjunction, option, kleene star, etc. Used in languages as Perl or Python and Unix commands as grep, . . . NLP FS Models

Example, acronym detection patterns acrophile acro 1 = re. compile('^([A-Z][, . -/_])+$') acro 2 = re. compile('^([A-Z])+$') acro 3 = re. compile('^d*[A-Z](d[A-Z])*$') acro 4 = re. compile('^[A-Z][A-Z]+[A-Za-z]+$') acro 5 = re. compile('^[A-Z]+[A-Za-z]+[A-Z]+$') acro 6 = re. compile('^([A-Z][, . -/_]){2, 9}('s|s)? $') acro 7 = re. compile('^[A-Z]{2, 9}('s|s)? $') acro 8 = re. compile('^[A-Z]*d[-_]? [A-Z]+$') acro 9 = re. compile('^[A-Z]+[A-Za-z]+[A-Z]+$') acro 10 = re. compile('^[A-Z]+[/-][A-Z]+$') NLP FS Models

Formal Languages Alphabet (vocabulary) concatenation operation * strings over (free monoid) Language L * Languages and grammars Regular Languages (RL) NLP FS Models

L, L 1 y L 2 are languages operations concatenation union intersection difference complement NLP FS Models

FSA < , Q, i, F, E> Q i Q F Q E Q ( { }) Q E: {d | d: Q ( { }) 2 Q} NLP FS Models alphabet finite set of states initial state final states set arc set transitions set

Example 1: Recognizes multiple of 2 codified in binary State 0: The string recognized till now ends with 0 State 1: The string recognized till now ends with 1 NLP FS Models

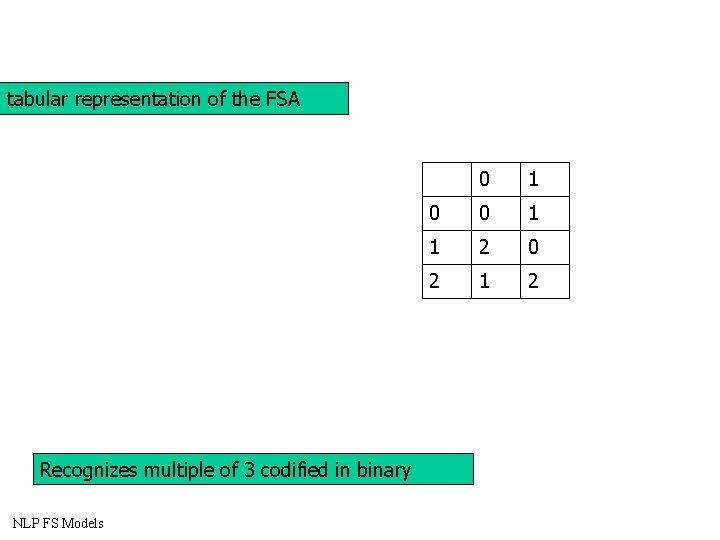
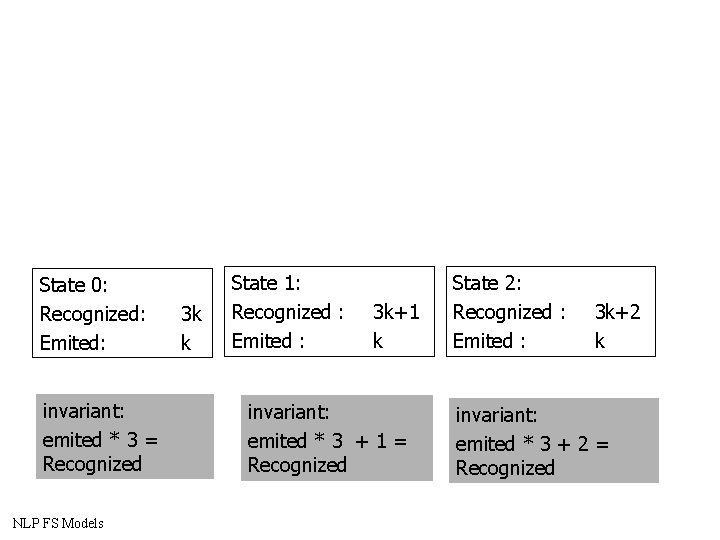
Example 2: Recognizes multiple of 3 codified in binary State 0: The string recognized till now is multiple of 3 State 1: The string recognized till now is multiple of 3 + 1 State 2: The string recognized till now is multiple of 3 + 2 The transition from a state to the following multiplies by 2 the current string and adds to it the current tag NLP FS Models

tabular representation of the FSA Recognizes multiple of 3 codified in binary NLP FS Models 0 1 0 0 1 1 2 0 2 1 2

Properties of RL and FSA Let A a FSA L(A) is the language generated (recognized) by A The class of RL (o FSA) is closed under union intersection concatenation complement Kleene star(A*) FSA can be determined FSA can be minimized NLP FS Models

The following properties of FSA are decidible w L(A) ? L(A) = * ? L(A 1) L(A 2) ? L(A 1) = L(A 2) ? Only the first two are for CFG NLP FS Models

Example of the use of closure properties Representation of the Lexicon Let S the FSA: Representation of the sentence with POS tags NLP FS Models

Restrictions (negative rules) FSA C 1 FSA C 2 We are interested on S - ( * • C 1 • *) - ( * • C 2 • *) = S - ( * • ( C 1 C 2) • *) NLP FS Models

From the union of negative rules we can build a Negative grammar G = * • ( C 1 C 2 … Cn) • *) NLP FS Models

The difference between the two FSA S -G will result on: Most of the ambiguities have been solved NLP FS Models

FST < 1, 2, Q, i, F, E> 1 2 input alphabet output alphabet Q i Q F Q E Q ( 1* 2 *) Q finite states set initial state final states set arcs set frequently 1 = 2 = NLP FS Models

Example 3 Td 3: division by 3 of a binary string 1 = 2 = ={0, 1} NLP FS Models

Example 3 input 0 11 110 1001 1100 1111 10010 output 0 01 010 0011 0100 0101 00110 NLP FS Models

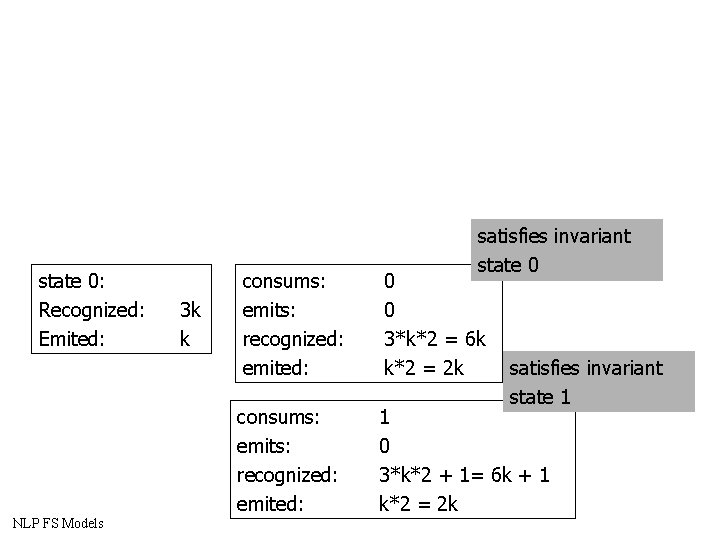
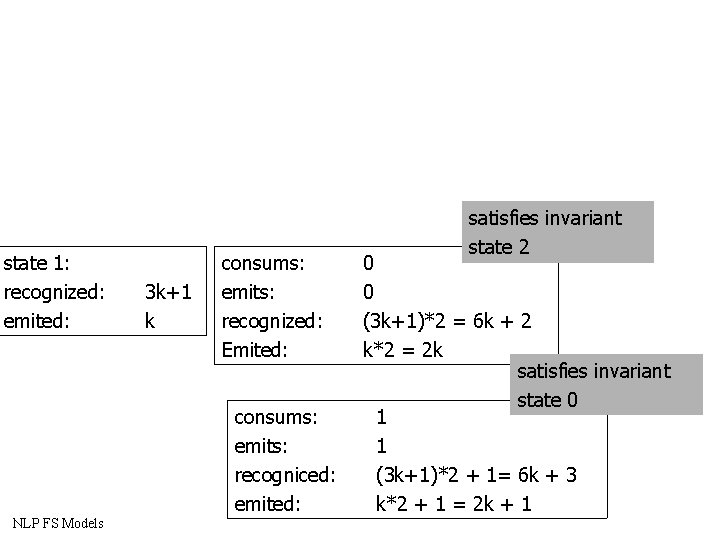
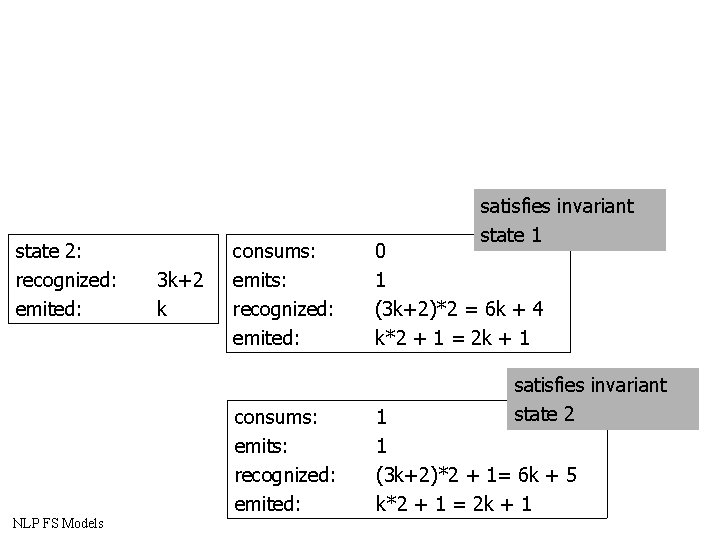
State 0: Recognized: Emited: invariant: emited * 3 = Recognized NLP FS Models 3 k k State 1: Recognized : Emited : 3 k+1 k invariant: emited * 3 + 1 = Recognized State 2: Recognized : Emited : 3 k+2 k invariant: emited * 3 + 2 = Recognized

state 0: Recognized: Emited: NLP FS Models 3 k k satisfies invariant state 0 consums: emits: recognized: emited: 0 0 3*k*2 = 6 k k*2 = 2 k consums: emits: recognized: emited: 1 0 3*k*2 + 1= 6 k + 1 k*2 = 2 k satisfies invariant state 1

state 1: recognized: emited: 3 k+1 k consums: emits: recognized: Emited: consums: emits: recogniced: emited: NLP FS Models satisfies invariant state 2 0 0 (3 k+1)*2 = 6 k + 2 k*2 = 2 k satisfies invariant state 0 1 1 (3 k+1)*2 + 1= 6 k + 3 k*2 + 1 = 2 k + 1

state 2: recognized: emited: 3 k+2 k consums: emits: recognized: emited: NLP FS Models satisfies invariant state 1 0 1 (3 k+2)*2 = 6 k + 4 k*2 + 1 = 2 k + 1 satisfies invariant state 2 1 1 (3 k+2)*2 + 1= 6 k + 5 k*2 + 1 = 2 k + 1

FSA associated to a FST < 1, 2, Q, i, F, E> FSA < , Q, i, F, E’> = 1 2 (q 1, (a, b), q 2) E’ (q 1, a, b, q 2) E NLP FS Models

FST 9 Projections of a FST T = < 1, 2, Q, i, F, E> First projection P 1(T) < 1, Q, i, F, EP 1> EP 1 = {(q, a, q’) | (q, a, b, q’) E} Second projection P 2(T) < 2, Q, i, F, EP 2> EP 2 = {(q, b, q’) | (q, a, b, q’) E} NLP FS Models

FST are closed under union invertion example: Td 3 -1 is equivalent to multiply by 3 composition example : Td 9 = Td 3 • Td 3 FST are not closed under intersection NLP FS Models

Application of a FST Traverse the FST in all forms compatible with the input (using backtracking if needed) until reaching a final state and generate the corresponding output Consider input as a FSA and compute the intersection of the FSA and the FST NLP FS Models

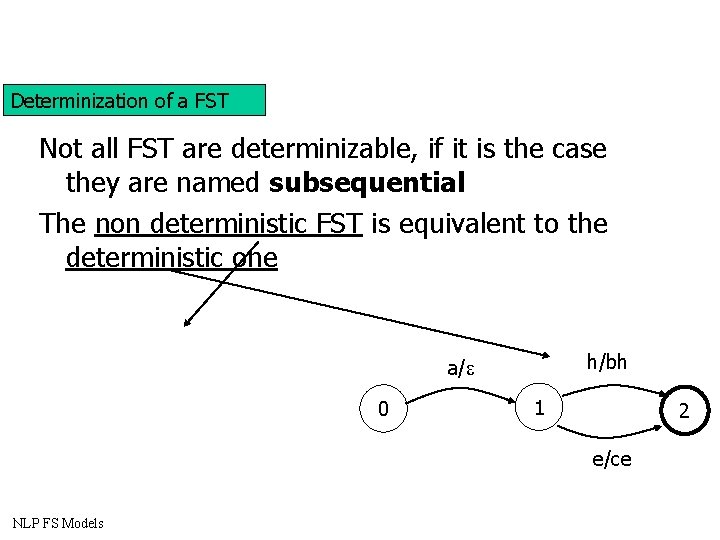
Determinization of a FST Not all FST are determinizable, if it is the case they are named subsequential The non deterministic FST is equivalent to the deterministic one h/bh a/ 0 1 2 e/ce NLP FS Models