Regular Expressions 1 REs Introduction u Regular expressions

Regular Expressions 1

RE’s: Introduction u. Regular expressions are an algebraic way to describe languages. u. They describe exactly the regular languages. u. If E is a regular expression, then L(E) is the language it defines. u. We’ll describe RE’s and their languages recursively. 2

RE’s: Definition u. Basis 1: If a is any symbol, then a is a RE, and L(a) = {a}. w Note: {a} is the language containing one string, and that string is of length 1. u. Basis 2: ε is a RE, and L(ε) = {ε}. u. Basis 3: ∅ is a RE, and L(∅) = ∅. 3

RE’s: Definition – (2) u. Induction 1: If E 1 and E 2 are regular expressions, then E 1+E 2 (the + can be read as OR) is a regular expression, and L(E 1+E 2) = L(E 1) L(E 2). u. Induction 2: If E 1 and E 2 are regular expressions, then E 1 E 2 (this notation can be read as concatenation) is a regular expression, and L(E 1 E 2) = L(E 1)L(E 2). (every combination of a string in E 1 concatenated with a string from E 2) 4

RE’s: Definition – (3) u. Induction 3: If E is a RE, then E* is a RE, and L(E*) = (L(E))*. Closure, or “Kleene closure” = set of strings w 1 w 2…wn, for some, indeterminate, n > 0, where each wi is in L(E). Note: when n=0, the string is ε. 5

Precedence of Operators u. Parentheses may be used wherever needed to influence the grouping of operators. u. Order of precedence is * (highest), then concatenation, then + (lowest). 6

Examples: RE’s u. L(01) = {01}. u. L(01+0) = {01, 0}. u. L(0(1+0)) = {01, 00}. w Note order of precedence of operators. u. L(0*) = {ε, 0, 000, … }. u. L((0+10)*(ε+1)) = all strings of 0’s and 1’s without two consecutive 1’s. 7

Equivalence of RE’s and Automata u. We need to show that for every RE, there is an automaton that accepts the same language. w Pick the most powerful automaton type: the ε-NFA. u. And we need to show that for every automaton, there is a RE defining its language. w Pick the most restrictive type: the DFA. 8

Converting a RE to an ε-NFA u. Proof is an induction on the number of operators (+, concatenation, *) in the RE. u. We always construct an automaton of a special form (next slide). 9

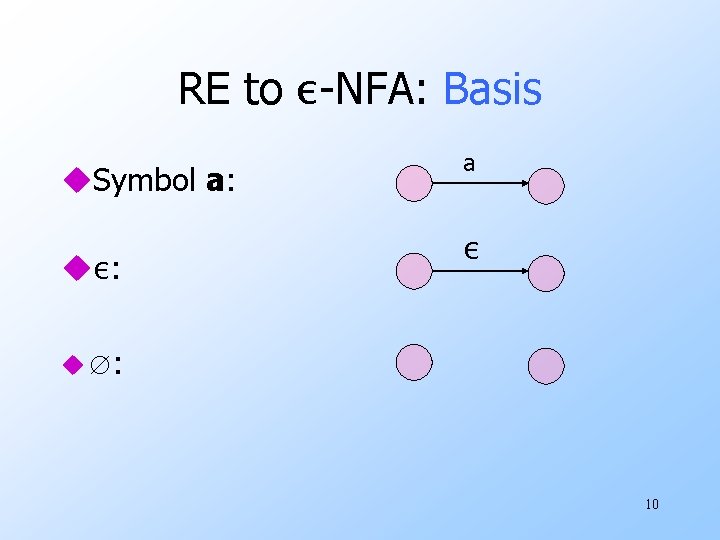
RE to ε-NFA: Basis u. Symbol a: uε: a ε u ∅: 10

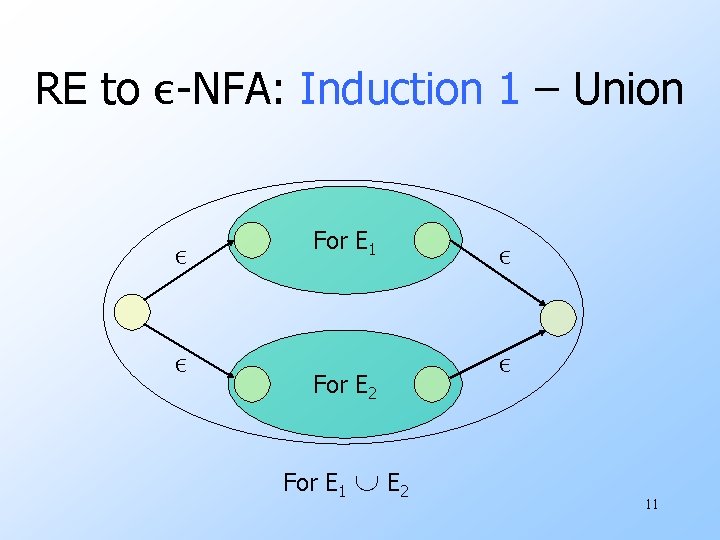
RE to ε-NFA: Induction 1 – Union ε ε For E 1 For E 2 For E 1 E 2 ε ε 11

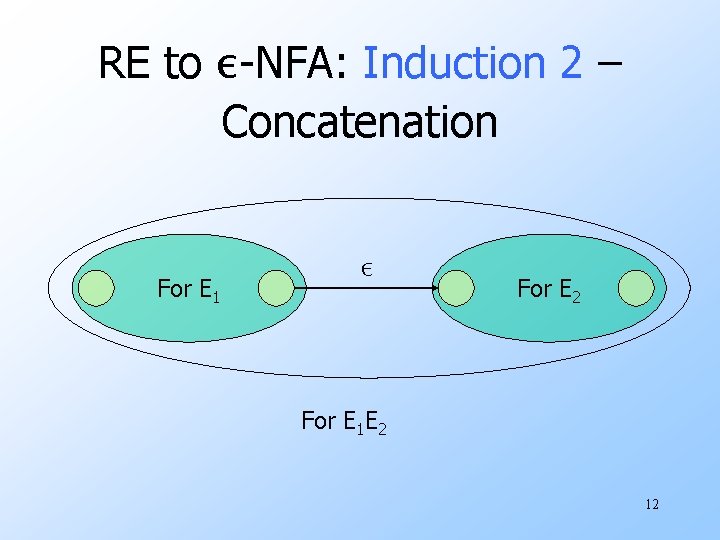
RE to ε-NFA: Induction 2 – Concatenation For E 1 ε For E 2 For E 1 E 2 12

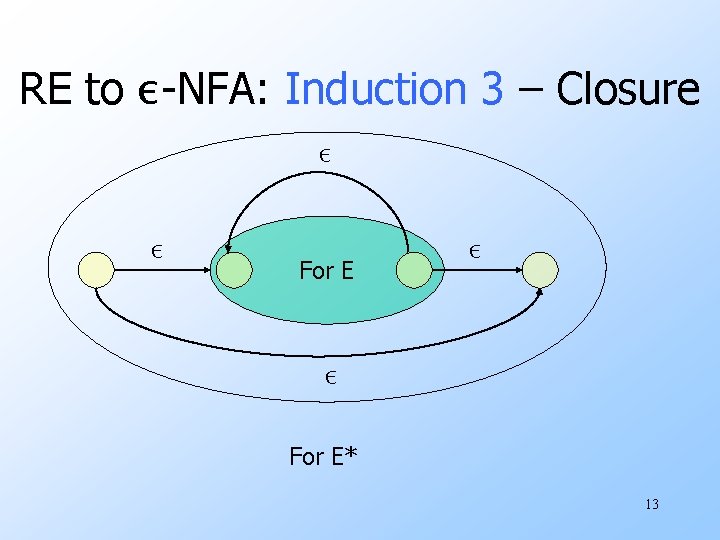
RE to ε-NFA: Induction 3 – Closure ε ε For E* 13

DFA-to-RE u. A strange sort of induction. u. States of the DFA are assumed to be 1, 2, …, n. u. We construct RE’s for the labels of restricted sets of paths. w Basis: single arcs or no arc at all. w Induction: paths that are allowed to traverse next state in order. 14

For Every FSM There is a Corresponding Regular Expression We’ll show this by construction. The key idea is that we’ll allow arbitrary regular expressions to label the transitions of an FSM.

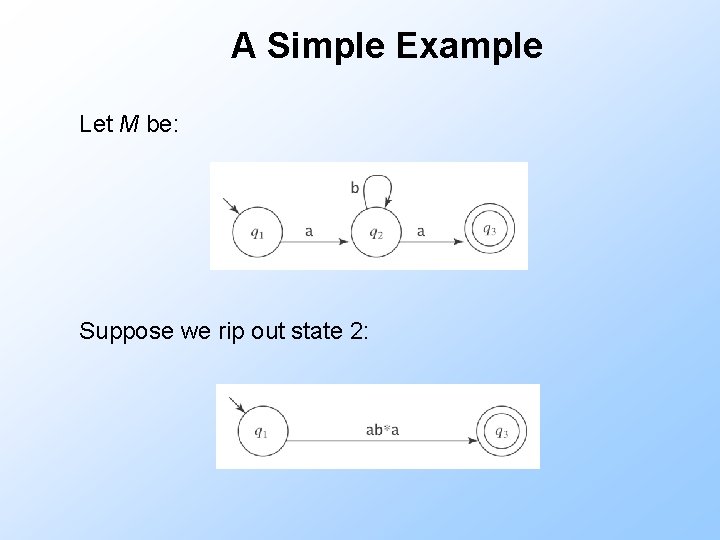
A Simple Example Let M be: Suppose we rip out state 2:

The Algorithm fsmtoregexheuristic(M: FSM) = 1. Remove unreachable states from M. 2. If M has no accepting states then return . 3. If the start state of M is part of a loop, create a new start state s and connect s to M’s start state via an -transition. 4. If there is more than one accepting state of M or there any transitions out of any of them, create a new accepting state and connect each of M’s accepting states to it via an -transition. The old accepting states no longer accept. 5. If M has only one state then return . 6. Until only the start state and the accepting state remain do: 6. 1 Select rip (not s or an accepting state). 6. 2 Remove rip from M. 6. 3 *Modify the transitions among the remaining states so M accepts the same strings. 7. Return the regular expression that labels the one remaining transition from the start state to the accepting state.

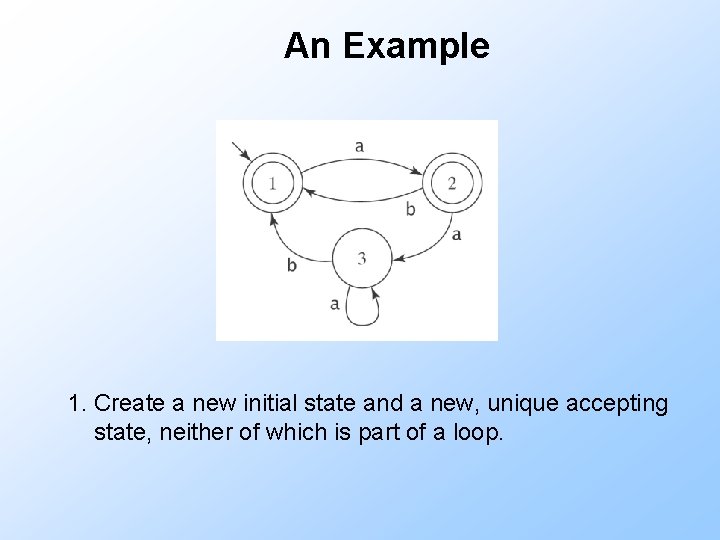
An Example 1. Create a new initial state and a new, unique accepting state, neither of which is part of a loop.

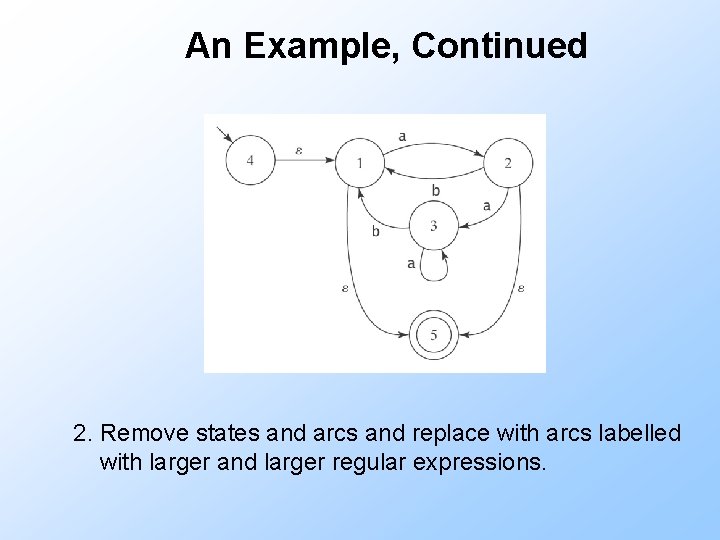
An Example, Continued 2. Remove states and arcs and replace with arcs labelled with larger and larger regular expressions.

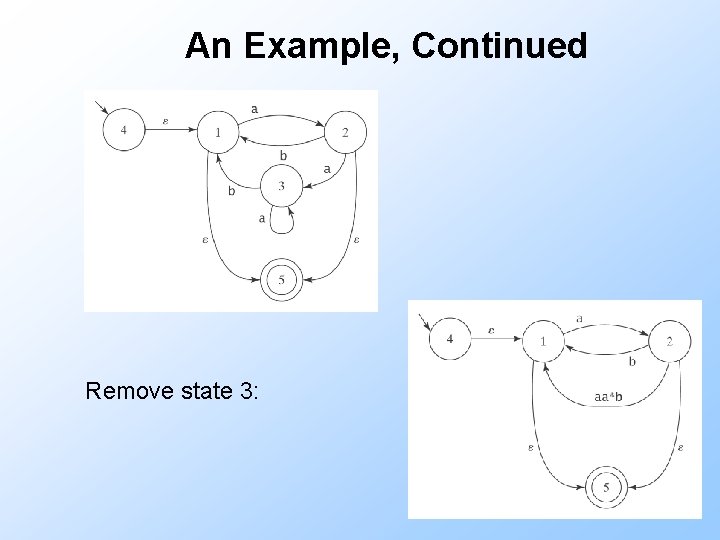
An Example, Continued Remove state 3:

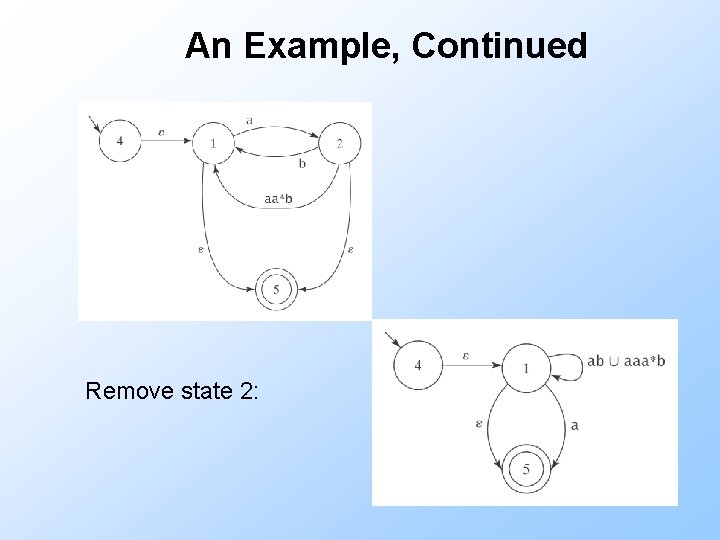
An Example, Continued Remove state 2:

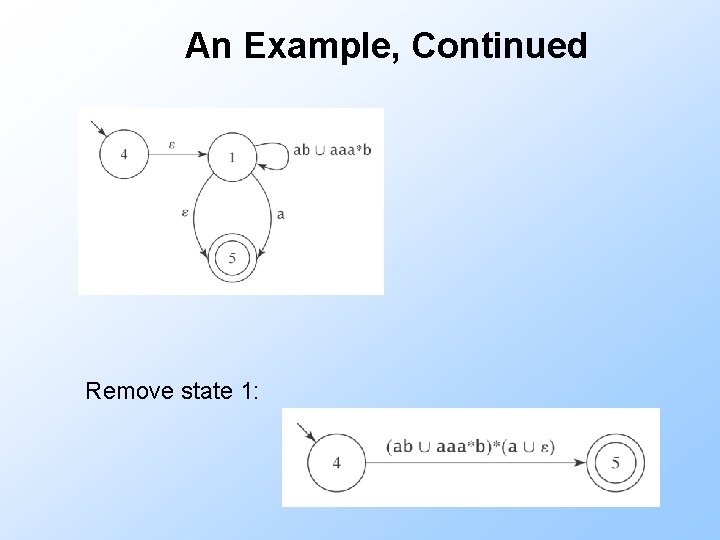
An Example, Continued Remove state 1:

Summary u. Each of the three types of automata (DFA, NFA, ε-NFA) we discussed, and regular expressions as well, define exactly the same set of languages: the regular languages. 23

Algebraic Laws for RE’s u. Union and concatenation behave sort of like addition and multiplication. w + is commutative and associative; concatenation is associative. w Concatenation distributes over +. w Exception: Concatenation is not commutative. 24

Identities and Annihilators u∅ is the identity for +. w. R + ∅ = R. u ε is the identity for concatenation. w εR = Rε = R. u ∅ is the annihilator for concatenation. w ∅R = R∅ = ∅. 25