REGULAR EXPRESSION AND LANGUAGES RL Recursive Definition RL

REGULAR EXPRESSION AND LANGUAGES

RL: Recursive Definition RL is defined recursively using three basic set operations as : 1. Ф is a regular language. 2. For each a ε ∑ , {a} is a RL 3. If L 1 , L 2 , …. Ln are RL , then L 1 U L 2 U L 3 U…. Ln is RL. 4. If L 1 , L 2 , …. Ln are RL , then L 1. L 2. L 3. …. Ln is RL. 5. If L is RL then L* is also RL 6. Anything which can be defined using rules 1 to 5 is considered as RL

Inductive Definition of RE Given a particular alphabet Σ and using three basic operations Union , Concatenation , and Kleen closure we can build RE representing Regular language. R is a regular expression if R is 1. , the empty string 2. a, for some a Σ 3. R 1+R 2, where R 1 and R 2 are RE. 4. R 1 R 2, where R 1 and R 2 are RE. 5. R 1*, where R 1 is a RE.

Precedence 1. “+” is Union operation 2. “ ” is Concatenation operation 3. “*” is Kleene Closure operation Closure has the highest precedence, followed by concatenation, followed by union.

RE : Examples 1. Strings of a’s with zero or more length. ie S={ε , a, aaa, aaaa, ………} This is written in terms of RE as : a* 2. Strings of length of one. S={a, b} RE = a+b 3. Strings made up of any combination of a’s and b’s of any length (zero length also) ie S={ ε, a, b, ab, ba, abab, baba, ……. } RE as : (a+b)*

Regular Set A set containing all the strings generated by a RE is known as Regular set. Example: Regular set for RE a* is given by { Є, a, aaa, …}

Regular Expressions Which of these are strings from the regular expression given: (00)*1(0+1)* 0, 1, 010, 000011, 0011010, 0000101010 0 No - must be at least one 1 1 Yes 010 No – must be two 0’s 0010 Yes 000011 Yes 0011010 Yes 0000101010 Yes

Algebraic laws For RE Need 1. To check whether two RE are equivalent 2. Simplify RE 3. To prove two RE define same language.

identities Let P, Q, R are RE then identity rules as : 1. Є. R = R. Є= R 2. �. R = R �= � 3. �+R =R

Idempotent law 1. Є* = Є 2. (Ф)*= Є 3. R+R = R 4. (R*)* = R* 5. R*R * = R* 6. R. R* = R*. R = R+

Commutative and Associative laws 1. P+Q = Q+ P 2. (P+Q) + R = p +(Q+R) 3. (PQ)R = P(QR)

Distributive laws 1. (P+Q)R=PR+QR RIGHT DISTRIBUTIVE 2. P(Q+R) = PQ + PR LEFT DISTRIBUTIVE

MISLENEOUS Let P, Q, R are RE then identity rules as : 1. Є +RR*= R* 2. (P+Q)*=(P*Q*)*=(P*+Q*)* 3. (PQ)*P=P(QP)*

Ardens Theorem : let P, Q be two RE over i/p set ∑. If P does not contain Є then there exists RE R such that R = Q+RP which has a unique solution as R =QP*

Equivalence of two RE Two RE, P and Q are equivalent (ie P=Q) if and only if P represents the same set of strings as Q does. R 1 = R 2 iff L(R 1) = L(R 2)

CONVRSION FA to RE 1. Arden’s theorem 2. State elimination method RE to FA 1. Indirect method 2. Direct method

Conversion DFA to RE Arden’s theorem is used to find RE from a TG(ie DFA), which must satisfy following properties: It should not have empty transitions It should have only one initial state say q 0

DFA to RE (Arden’s theorem) Following steps are used for conversion 1. Let q 1 be the initial state 2. There are q 2, q 3, …qn number of states. The final state may be qj where j<=n 3. Let represents the transition from qj to qi ji and it is the RE representing the set of labels of edges from 4. qj to qi When there is no edge ji= �

Hence for every state qi we write a RE as qi= q 1 1 i + q 2 2 i + … + qn (+ Є only for start state ) ni Using above we get the following equations in q 1, q 2, q 3, …qn. q 1= q 1 11 + q 2= q 1 12 + q 2 qn= q 1 1 n + q 2 21 22 2 n + … + qi + … + qn (+ Є only for start state ) n 1 n 2 nn

By repeatedly applying substitution and Arden’s theorem , we get final RE

DFA to RE: State Elimination In this approach states of the DFA are removed one by one until we left with only start and final state. For each removed state RE is generated. This newly generated RE acts as a i/p for the state which is next to removed state.

DFA to RE: State Elimination If there are multiple edges from one node to another, these are unified into single edge that contains union of i/ps.

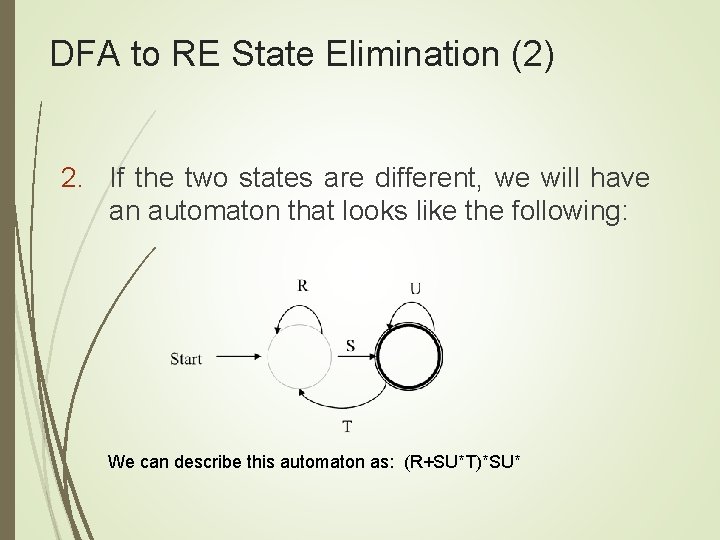
DFA to RE State Elimination (2) 2. If the two states are different, we will have an automaton that looks like the following: We can describe this automaton as: (R+SU*T)*SU*

DFA to RE State Elimination (3) 3. If the start state is also an accepting state, then we must also perform a state elimination from the original automaton that gets rid of every state but the start state. This leaves the following: We can describe this automaton as simply R*.

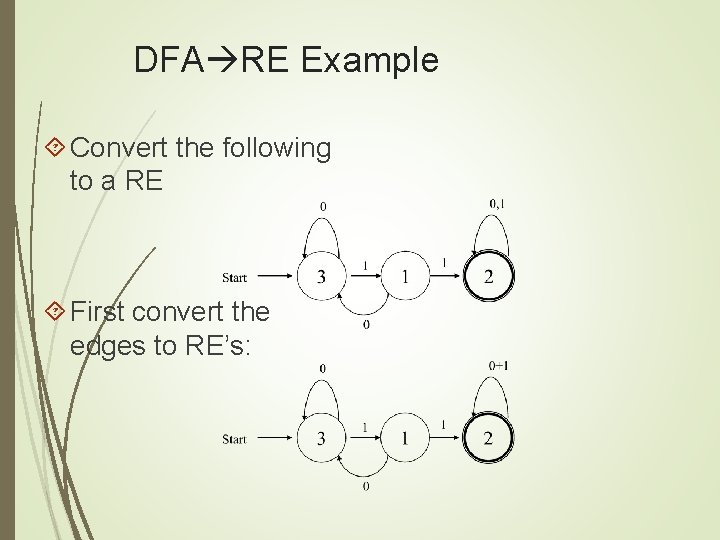
DFA RE Example Convert the following to a RE First convert the edges to RE’s:

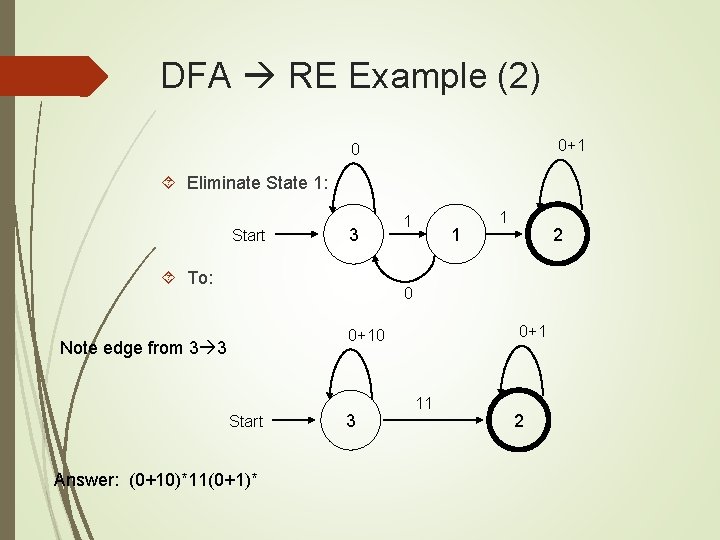
DFA RE Example (2) 0+1 0 Eliminate State 1: Start 3 To: 1 1 1 2 0 0+10 Note edge from 3 3 Start Answer: (0+10)*11(0+1)* 3 11 2

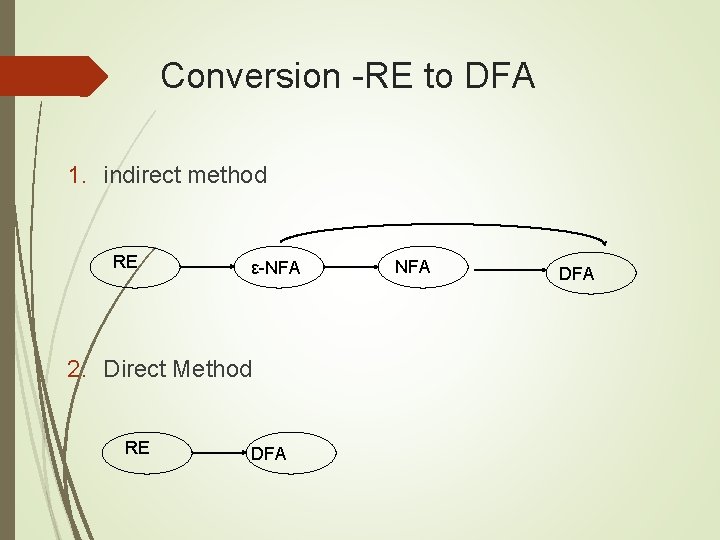
Conversion -RE to DFA 1. indirect method RE ε-NFA 2. Direct Method RE DFA NFA DFA

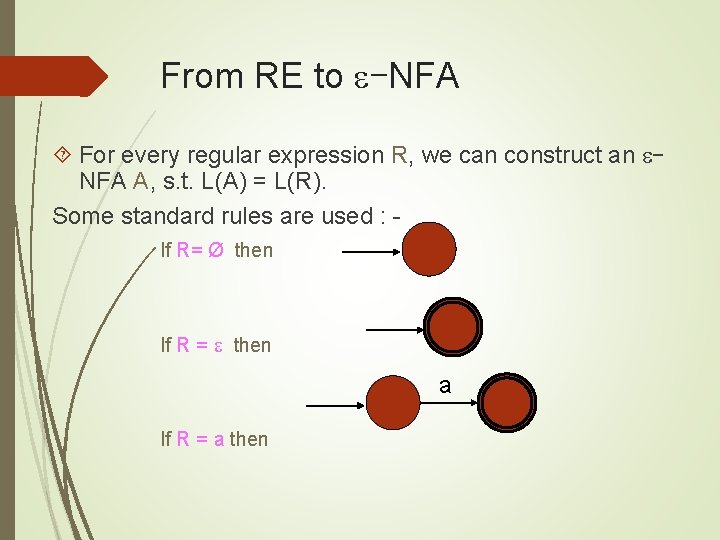
From RE to -NFA For every regular expression R, we can construct an NFA A, s. t. L(A) = L(R). Some standard rules are used : If R= Ø then If R = then a If R = a then

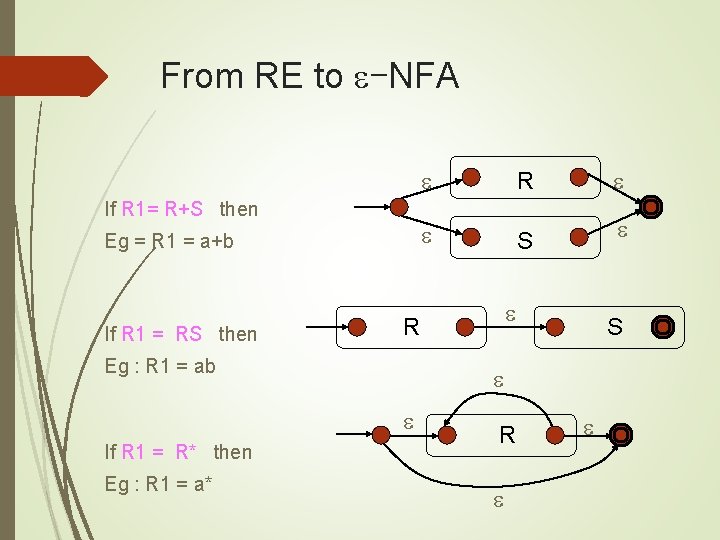
From RE to -NFA If R 1= R+S then Eg = R 1 = a+b If R 1 = RS then S S Eg : R 1 = a* R R Eg : R 1 = ab If R 1 = R* then R

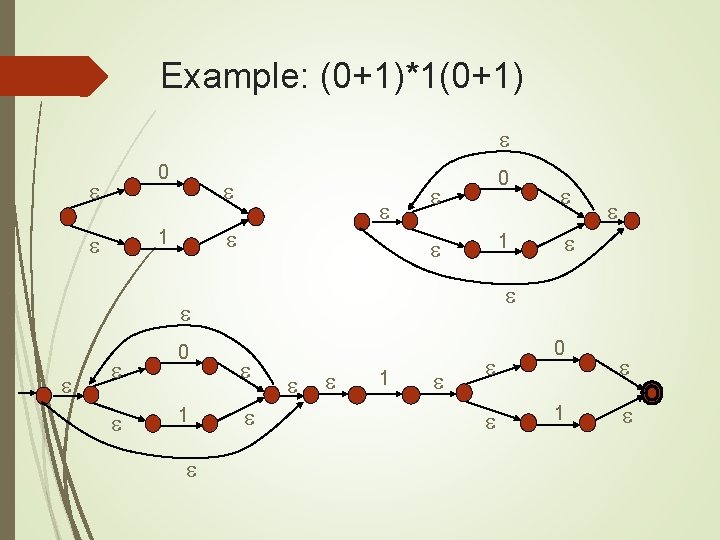
Example: (0+1)*1(0+1) 0 1 0 1 0 1 0 1

Example (a+b)*aba

Limits on the Power of FA 1. An FA is limited on finite memory, i. e. finite set of states. It does not have the capacity to remember arbitrary large amt of information. 2. Finite automata can’t count.

Limits on the Power of FA Consider the language i. e. , a bunch of a’s followed by an equal number of b’s No finite automaton accepts this language. Can we prove this?

Non-Regular Languages Is this language regular? L = {ww. R | w ε (a, b)} = all palindrome words L = {w | w has equal numbers of ‘ 0’ and ‘ 1’}

Pumping Lemma If L is a regular language, then there is an integer n>=1 such that any string w in L with |w| >= n, can be written as w = xyz, where: 1. |y| > 0 2. |xy| <= n 3. For all i >= 0, xyiz is also in L

Use of Pumping Lemma Use pumping lemma to prove that L is not regular. Steps : 1. Assume L is regular; 2. then there exists a pumping length n; 1. We may not know what n is, but we can work the rest of the “game" with n as a parameter. 3. select a string w L such that |w|>=n; 4. Applying the PL, we know w can be broken into xyz, satisfying the PL properties 5. We derive a contradiction by picking i>=0 such that xyiz is not in L (whatever x, y, z are)

Applications of FA Compilers Text Editors