Regresszi Mestersges neuronhlk mrc 12 Regresszi Regresszi Felgyelt

Regresszió, Mesterséges neuronhálók márc. 12.

Regresszió

Regresszió – Felügyelt (induktív) tanulás: tanító halmaz alapján olyan modell tanulása ami korábban nem látott példákon is helyesen működik. – Regresszió: folytonos érték előrejelzése. (statisztika „regresszió analízise” hasonló technikákat használ, de más a cél)

Regresszió Tanító adatbázis: {xi, ri} riϵR Célfüggvény: „Legkisebb négyzetes hiba”

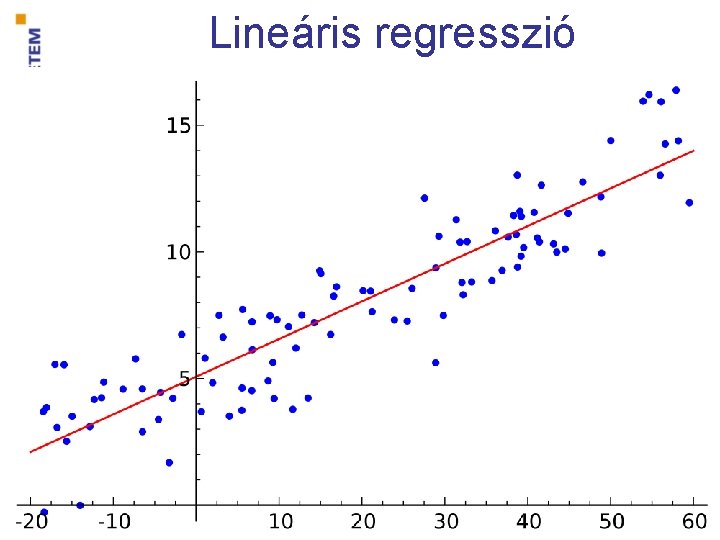
Lineáris regresszió

Lineáris regresszió g(x) = w 1 x + w 0 gradiense 0 ha

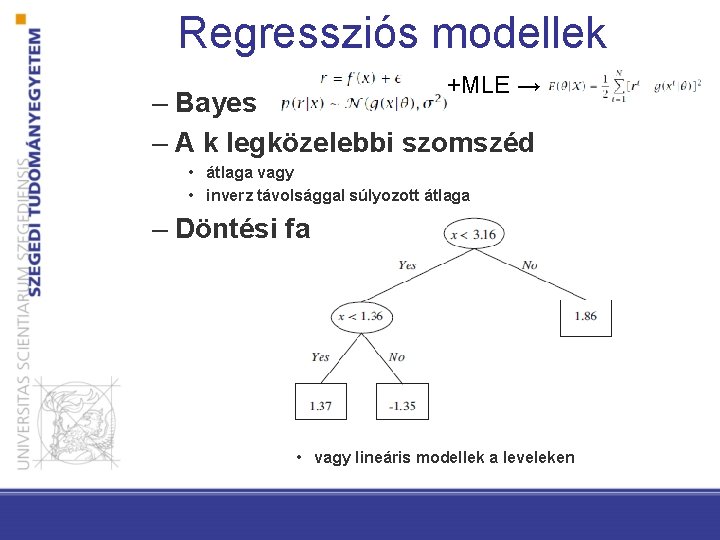
Regressziós modellek +MLE → – Bayes – A k legközelebbi szomszéd • átlaga vagy • inverz távolsággal súlyozott átlaga – Döntési fa • vagy lineáris modellek a leveleken

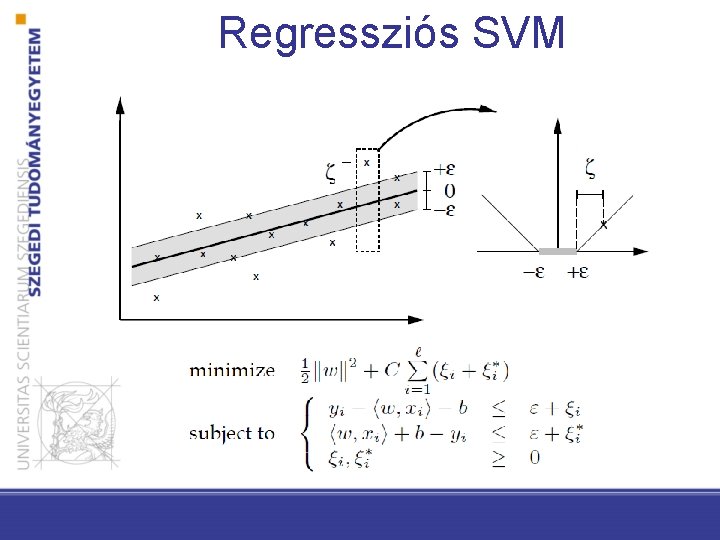
Regressziós SVM

Neuronhálók

Bevezetés • Mesterséges neuronhálók (artificial neural networks) • Az információfeldolgozás a biológiai idegrendszer (pl. az emberi agy) működését próbálja utánozni • Struktúra: nagyszámú, erősen összefüggő, együttműködő processzáló elem (idegsejtek(neuronok)) • Az emberekhez hasonlóan, tanulnak a tapasztalatokból (példák segítségével)

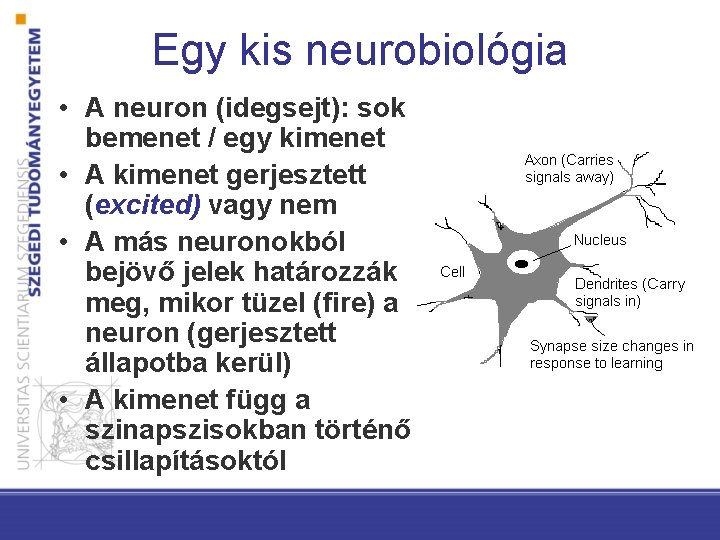
Egy kis neurobiológia • A neuron (idegsejt): sok bemenet / egy kimenet • A kimenet gerjesztett (excited) vagy nem • A más neuronokból bejövő jelek határozzák meg, mikor tüzel (fire) a neuron (gerjesztett állapotba kerül) • A kimenet függ a szinapszisokban történő csillapításoktól

Matematikai megfogalmazás Feltevésünk: a neuron a bemenetek súlyozott átlagát számítja ki, és az eredményt összehasonlítja egy küszöbértékkel. Ha nagyobb, akkor a kimenet 1 (tüzel, gerjesztett állapotba kerül) különben -1.

Néhány adat • Neuronok száma az agyban: ~ 1011 • Egy neuron átlagosan 104 másikkal van kapcsolatban • Leggyorsabb kapcsolási idő: 10 -3 másodperc • Arcfelismerési idő: 10 -1 másodperc

Motiváció (gépi tanulási szemmel) • Cél: osztályozás elvégzése nem-lineáris összefüggések tanulásával – Sok olyan probléma van, ahol a lineáris diszkriminancia nem megfelelő eredményt ad – A fő nehézség a megfelelő nemlineáris függvény megtalálása – A “nyers erő” megközelítésnél valamilyen függvénycsaládot választunk(például polinomokat)

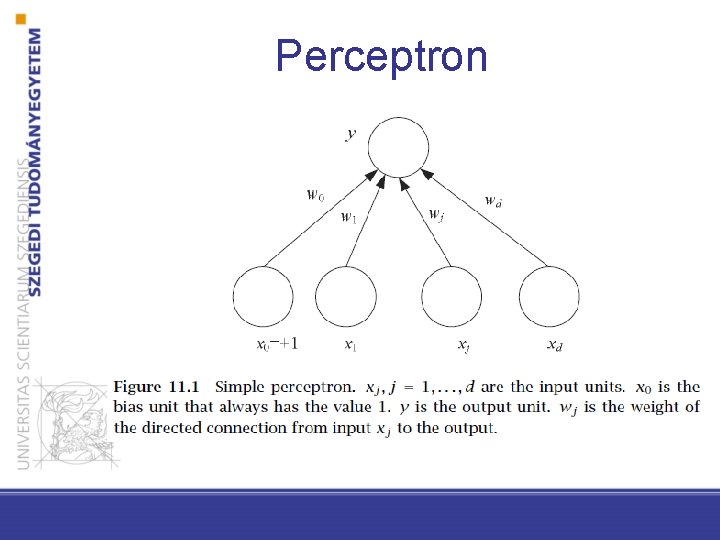
Perceptron

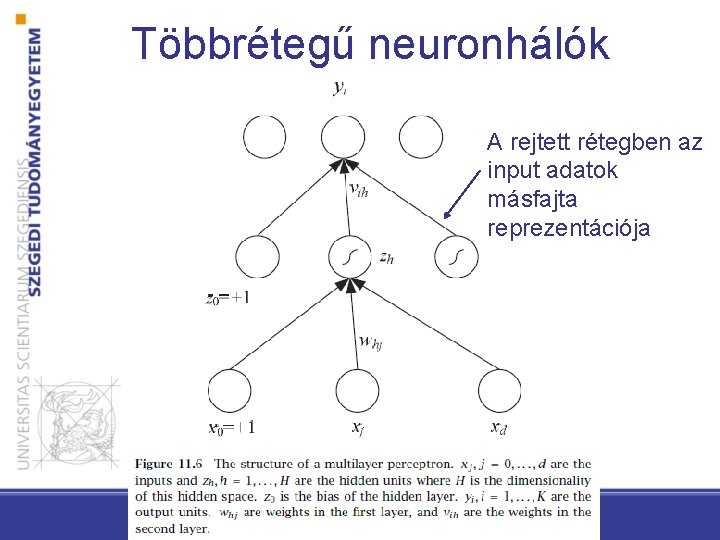
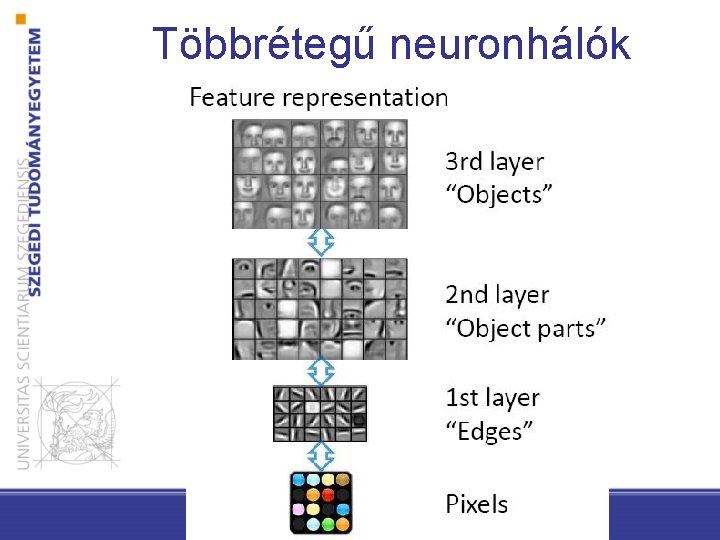
Többrétegű neuronhálók A rejtett rétegben az input adatok másfajta reprezentációja

Többrétegű neuronhálók

Előrecsatolt (feedforward) háló • Kapcsolat csak a rákövetkező réteg irányában van • a rétegek között módosítható súlyokkal ellátott kapcsolatok vannak • tüzelés pl: előjel függvény • Egy háromrétegű neuronháló egy input rétegből, egy rejtett rétegből és egy kimenet rétegből áll

Eltolás • Van egy konstans egységünk is, amelyik minden rejtett egységhez (neuronhoz) hozzá van kötve. Ennek bemeneti értéke mindig 1. • Egy neuron (hálózatának) aktivációja: ahol i az input egységeket indexeli, j a rejtett egységeket; wji jelöli az i inputból jövő kapcsolat súlyát a j rejtett neuronnál.

Aktivációs-függvény Minden rejtett egység kibocsátja az aktiválásának valamely nemlineáris függvényét (aktivációs-függvény), azaz yj = f(netj) (A több rétegű lineáris függvény még lineáris) Előjel függvény: oi 1 0 Tj netj

Differenciálható aktivációs függvény • Differenciálható, nem-lineáris kimeneti függvény kell a hatékony tanuláshoz (gradiens alapú módszerek) • A leggyakoribb megoldás a szigmoid “logikai” függvény használata: 1 0 Tj netj Használják még a tanh vagy a Gauss függvényt is

Kimeneti egységeknél (hasonlóan) az aktiváció: ahol a k az output réteg egységeit, az n. H pedig a rejtett egységek számát jelöli • Bináris osztályozás: előjel függvény • Többosztályos osztályozás: minden osztályra egy kimenet, legnagyobb aktivációs értékűt választjuk (diszkriminancia fgv. ) • Regresszió: aktivációs érték a predikció

– Az y 1 rejtett egység számolja a következő felületet: 0 y 1 = +1 x 1 + x 2 + 0. 5 - Az y 2 pedig a következőt: x 1 + x 2 -1. 5 < 0 y 1 = -1 x 1 OR x 2 0 y 2 = +1 < 0 y 2 = -1 x 1 AND x 2 – A végső kimeneti egység jelei: z 1 = 0. 7 y 1 -0. 4 y 2 - 1, sgn(z 1) pontosan akkor lesz 1, ha y 1 =1, y 2 = -1, ami éppen a kívánt függvényünk (x 1 OR x 2 ) AND NOT(x 1 AND x 2)

Általános (3 rétegű) előrecsatolt háló (c kimeneti egység) • – A rejtett egységek segítségével bonyolultabb nemlineáris függvényeket is kifejezhetünk, bővítve az osztályozási lehetőségeket – Megengedhetjük, hogy a kimeneten és a rejtett rétegeken levő aktivációs függvények különbözőek legyenek, sőt minden egységhez is különböző tartozhat

Kolmogorov tétele: minden korlátos folytonos függvény előállítható három rétegű hálózattal. • A 2 d+1 darab rejtett egység mindegyike inputként d nem-lineáris függvény összegét kapja, minden xi tulajdonságból egyet • Minden rejtett egység bemenetének nemlineáris függvényét adja outputként • Az output egység a rejtett egységek hozzájárulásainak összegét adja Sajnos, de: Kolmogorov tétele nagyon keveset mond arról, hogyan találjuk meg a bemeneti adatokból a megfelelő nemlineáris függvényeket

Többrétegű neuronháló tanítása Visszaterjesztés (backpropagation)

Tanulás neuronhálóknál • A hálózat topológiáját előre adottnak tekintjük • Minden neuronnál ugyanaz, előre rögzített aktivációs fgv. • Tapasztalat: példák (tanító adatok) • Tanulás = súlyok kalibrálása • on-line tanulás (több epoch)

Tanulás neuronhálóknál – Predikció (előrecsatolás) Ilyenkor adunk egy mintát az inputon, és ezt átszámoljuk a hálózaton – a végén a kimeneten értéke(ke)t kapunk – Tanulás (visszaterjesztés) Ilyenkor az adott mintát arra használjuk, hogy módosítsuk a súlyokat úgy, hogy a számított és elvárt kimenetek különbsége csökkenjen

Tanulás neuronhálóknál • 3 rétegű hálózatokat vizsgálunk (könnyen megérthető, Kolmogorov tétele) • A visszaterjesztés lényege: minden rejtett egységhez ki tudjuk számolni annak hibáját (érzékenységét), és ezzel egy tanulási eljárást ad a rétegek közti súlyokra

• Legyen tk a kívánt k-ik kimenet, továbbá zk a k-ik számított kimenet (k = 1, …, c) tovább w jelölje a hálózat súlyait • Hiba: – A visszaterjesztés szabály a gradiens módszeren alapul • A súlyok kezdőértékei véletlen számok, és a hiba csökkentésének irányában változnak:

Hiba visszaterjesztés A rejtett és kimenet rétegek közötti súlyok hibái: ahol a k. kimeneti neuron érzékenységének definíciója: és megadja, hogyan változik a teljes hiba az egység hálózatának aktivációjával

Mivel netk = wkty, kapjuk: másrészt: Következmény: a súlyok változtatásának szabálya (a rejtett-kimenet rétegre): wkj = kyj = (tk – zk) f’ (netk)yj

A bemenet és rejtett rétegek közötti súlyok hibái:

Az előzőhöz hasonlóan definiáljuk a rejtett réteg érzékenységét: Következmény: az input-rejtett rétegek közötti súlyokra vonatkozó tanulási szabály:

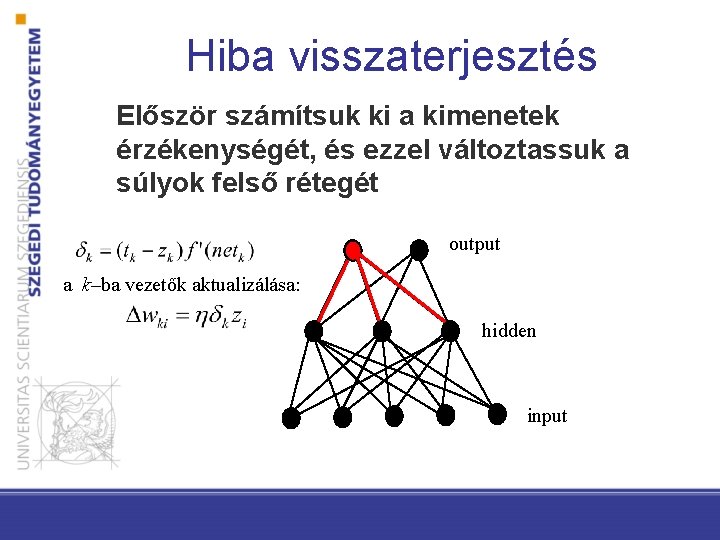
Hiba visszaterjesztés Először számítsuk ki a kimenetek érzékenységét, és ezzel változtassuk a súlyok felső rétegét output a k–ba vezetők aktualizálása: hidden input

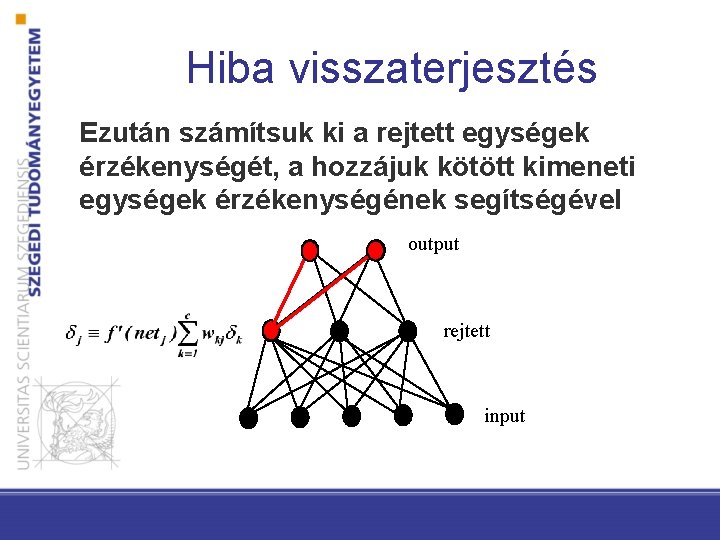
Hiba visszaterjesztés Ezután számítsuk ki a rejtett egységek érzékenységét, a hozzájuk kötött kimeneti egységek érzékenységének segítségével output rejtett input

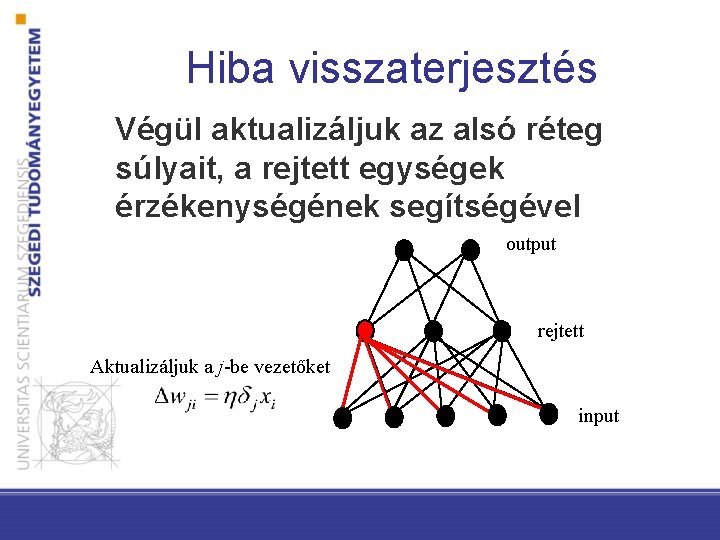
Hiba visszaterjesztés Végül aktualizáljuk az alsó réteg súlyait, a rejtett egységek érzékenységének segítségével output rejtett Aktualizáljuk a j-be vezetőket input

Véletlenszerűen választott súlyokkal kezdve, a sztochasztikus visszaterjesztés algoritmus: Begin inicializálni: n. H; w, kritérium , , m 0 do m m + 1 xm véletlenül választott minta wji + jxi; wkj + kyj until || J(w)|| < return w End

Megállási feltétel • Az algoritmus leáll, ha a J(w) kritériumfüggvény változása kisebb az előre adott küszöbértéknél • Más, ennél jobb megállási kritériumot is használnak, pl. eddig egy mintára néztük a hibát, de jobb lenne a teljes tanító halmazra meghatározni:

Megállás validációs halmaz alapján – Kezdetben a teljes tanítóhalmazhoz tartozó hiba nagy, a tanítás során csökken – Az egy mintára eső hiba a tanítási halmaz méretétől és a hálózat kifejező erejétől függ – Egy független tesztelő halmazon az átlagos hiba általában nagyobb, mint a tanító-halmazon kapott – növekedhet és csökkenhet is – Egy validációs halmazt szokás annak eldöntésére használni, hogy mikor állítsuk meg a tanítást – általában nem akarjuk túltanítani (overfit) a hálózatot, és ezzel csökkenteni az általánosító képességét – a tanítást a validációs halmazon elért minimális hibánál állítjuk meg

Megjegyzések • Nem biztos, hogy zérus hibához konvergál – lokális optimumhoz is tarthat, vagy oszcillálhat • A gyakorlatban nagyon sok nagy problémánál kicsi hibához tartozó megoldást ad • Sokezerszer lefuttatandó ciklus lehet, nagyon hosszú tanítási idővel • A lokális minimál-megoldások elkerüléséhez többszöri futtatás, véletlen kezdősúlyokkal – A legkisebb hibához tartozó megoldást vegyük – Vagy valamilyen többségi szavazással válasszuk ki a megoldást

Teljesítőképesség • Boole függvények: Bármely Boole függvény reprezentálható három rétegű hálóval, elegendően sok rejtett egységgel. • Folytonos függvények: bármely korlátos folytonos függvény tetszőlegesen kicsi hibával közelíthető három rétegű hálózattal – Sigmoid függvények használhatók bonyolultabb függvények előállításához • Tetszőleges függvények: négy rétegű hálózattal tetszőleges függvény tetszőleges pontossággal közelíthető

Megjegyzések • Hány rejtett neuron kell? – ha kevés rossz reprezentáció – ha sok túltanulás – validációs halmaz. . . • Mi az optimális toplológia? – priori tudás • Tanulási arány!?

A diasor hátralévő részét nem adtam le órán így vizsgán sem kérdezem!

Kitekintés

Neuronhálók • Perceptron: az első algoritmus az ötvenes évekből (egyrétegű háló) • Visszaterjesztés algoritmus: többrétegű hálózatok, a hetvenesnyolcvanas években fejlesztették ki őket • Mély gépi tanulás (deep learning): utóbbi 5 -6 évben új virágkor

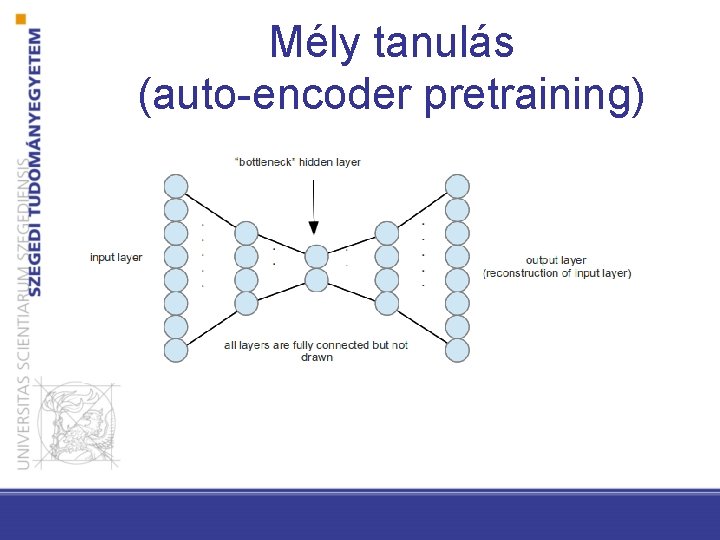
Mély tanulás (auto-encoder pretraining)

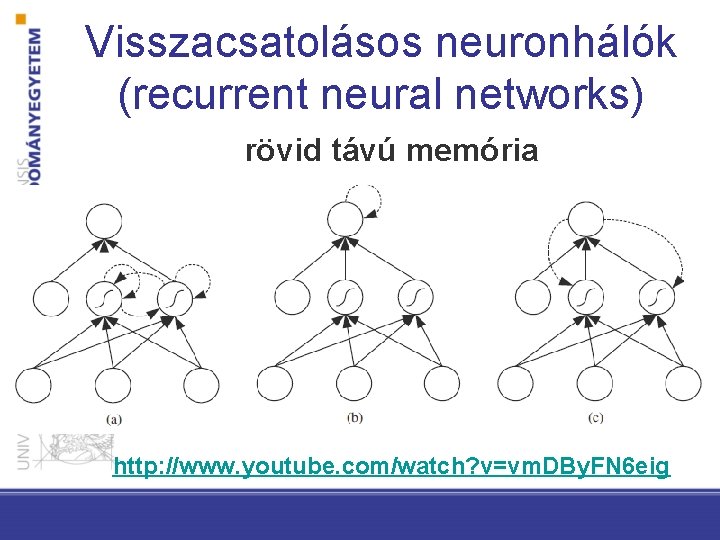
Visszacsatolásos neuronhálók (recurrent neural networks) rövid távú memória http: //www. youtube. com/watch? v=vm. DBy. FN 6 eig