Regression with 2 IVs Generalization of Regression from

Regression with 2 IVs Generalization of Regression from 1 to 2 Independent Variables

Questions • What happens to b • Write a raw score weights if we add new regression equation variables to the with 2 IVs in it. regression equation that • What is the are highly correlated with ones already in the difference in equation? interpretation of b • Why do we report beta weights in simple weights (standardized b regression vs. weights)? multiple regression?

More Questions • What are three • Write a regression factors that equation with beta influence the weights in it. standard error of the • How is it possible to b weight? have a significant r • Describe R-square and nonin two different significant b ways, that is, using weights? two distinct formulas. Explain the formulas.

Equations 1 IV. Define terms. Multiple IVs. One score, 1 intercept; 1 error; many slopes. Predicted value. Recall slope and intercept for 1 IV: Sum of cross-products.

Equations (2) Note: b weights use SSx 1, SSx 2, and all 3 cross products. Unlike slopes, the intercept is a simple extension of the 1 IV case.

Numerical Example Chevy mechanics; mechanical aptitude & conscientiousness. Find sums. Job Perf Y Mech Apt X 1 Consc X 2 X 1*Y X 2*Y X 1*X 2 1 40 25 1000 2 45 20 90 40 900 1 38 30 1140 3 58 38 174 114 2204 Y X 1 X 2 X 1*Y X 2*Y X 1*X 2 65 1038 655 3513 2219 34510 20 20 20 N 3. 25 51. 9 32. 75 175. 65 110. 95 1725. 5 M 1. 25 7. 58 5. 24 84. 33 54. 73 474. 60 SD 29. 75 1091. 8 521. 75 Sum USS Note. Only some of the data are shown. Size problem in Powerpoint.

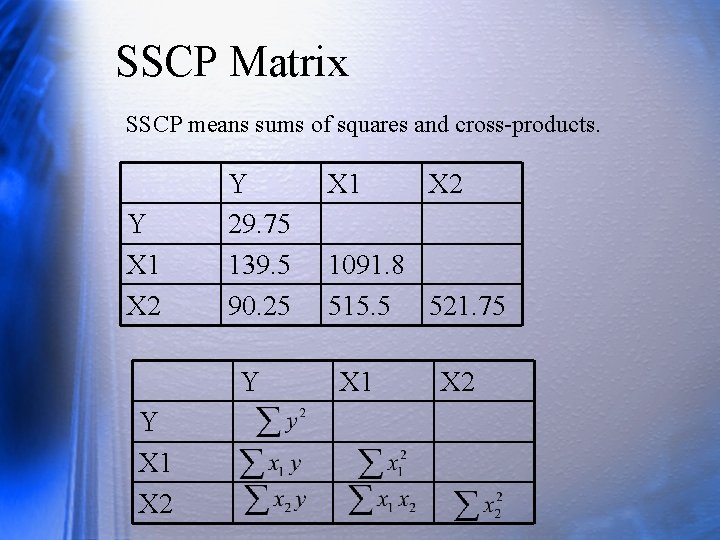
SSCP Matrix SSCP means sums of squares and cross-products. Y X 1 X 2 Y 29. 75 139. 5 90. 25 Y Y X 1 X 2 1091. 8 515. 5 521. 75 X 1 X 2

Find Estimates Y X 1 (MA) Y (Perf) 29. 75 X 1 139. 5 1091. 8 X 2 90. 25 515. 5 X 2 (Consc) SSCP 521. 75 Predicted job performance as a function of test scores.

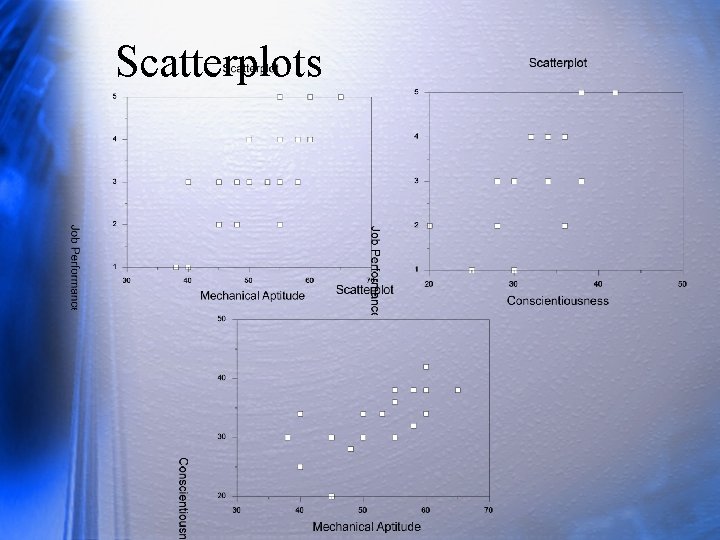
Scatterplots

Scatterplot 2

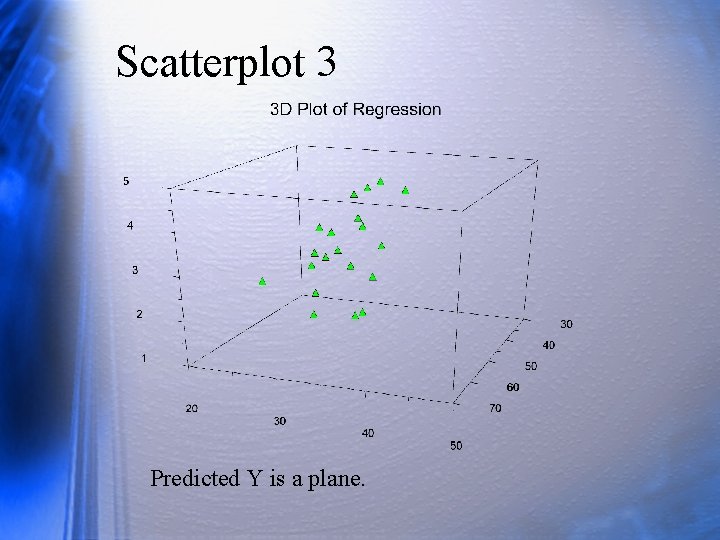
Scatterplot 3 Predicted Y is a plane.

2 R Y is linear function of Xs plus error. Use capital R for multiple regression. R 2 is the proportion of variance in Y due to regression. Note: N=19; lost 1. Y 2 1 3 2 3 3 4 4 3 5 3 3 2 4 5 5 5 4 3 M = 3. 25 X 1 45 38 50 48 55 53 55 58 40 55 48 45 55 60 60 60 65 50 58 51. 9 X 2 20 30 30 28 30 34 36 32 34 38 28 30 36 34 38 42 38 34 38 32. 75 Y' 1. 54 1. 81 2. 84 2. 50 3. 28 3. 45 3. 80 3. 71 2. 33 3. 98 2. 50 2. 41 3. 80 4. 06 4. 41 4. 76 4. 84 3. 19 4. 24 3. 25 Resid 0. 46 -0. 81 0. 16 -0. 50 -0. 28 -0. 45 0. 20 0. 29 0. 67 1. 02 0. 50 0. 59 -1. 80 -0. 06 0. 59 0. 24 0. 16 0. 80 -1. 24 0 V = 1. 57 57. 46 27. 46 1. 05 0. 52 USS=29. 83 19. 95 9. 42

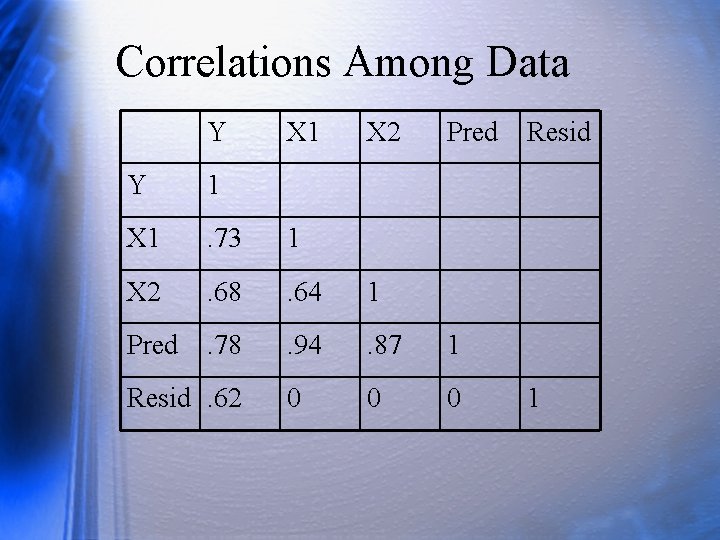
Correlations Among Data Y X 1 X 2 Pred Y 1 X 1 . 73 1 X 2 . 68 . 64 1 Pred . 78 . 94 . 87 1 0 0 0 Resid. 62 Resid 1

Excel Example Grab from the web under Lecture, Excel Example.

Review • Write a raw score regression equation with 2 IVs in it. Describe terms. • Describe a concrete example where you would use multiple regression to analyze the data. • What does R 2 mean in multiple regression? • For your concrete example, what would an R 2 of. 15 mean? • With 1 IV, the IV and the predicted values correlate 1. 0. Not so with 2 or more IVs. Why?

2 Significance Test for R When the null is true, result is distributed as F with k and (N-k-1) df. In our example, R 2 =. 61, k = 2 and N = 20. F(α=. 05, 2, 17)=3. 59.

The Problem of Variable Importance With 1 IV, the correlation provides a simple index of the ‘importance’ of that variable. Both r and r 2 are good indices of importance with 1 IV. With multiple IVs, total R-square will be the sum of the individual IV r 2 values, if and only if the IVs are mutually uncorrelated, that is, they correlate to some degree with Y, but not with each other. When multiple IVs are correlated, there are many different statistical indices of the ‘importance’ of the IVs, and they do not agree with one another. There is no simple answer to questions about the importance of correlated IVs. Rathere are many reasonable answers depending on what you mean by importance.

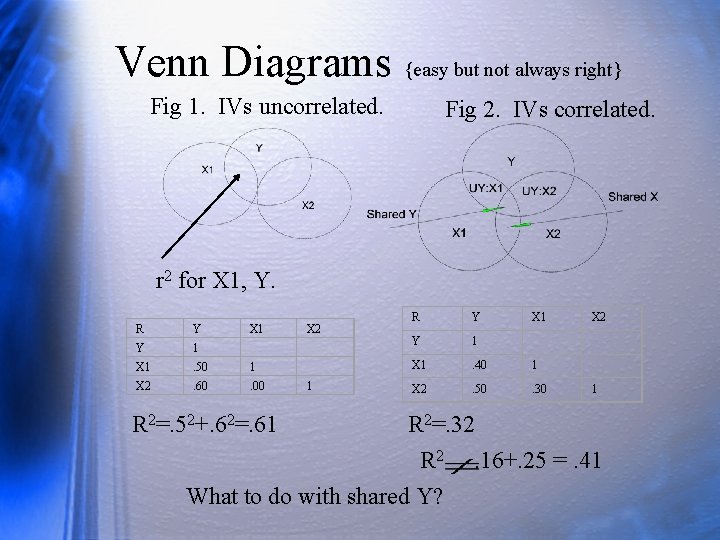
Venn Diagrams {easy but not always right} Fig 1. IVs uncorrelated. Fig 2. IVs correlated. r 2 for X 1, Y. R Y X 1 X 2 Y 1 X 1 . 40 1 1 X 2 . 50 . 30 1 R Y X 1 X 2 Y 1 X 1 . 50 1 X 2 . 60 . 00 R 2=. 52+. 62=. 61 R 2=. 32 R 2 . 16+. 25 =. 41 What to do with shared Y?

More Venn Diagrams Desired state Typical state In a regression problem, we want to predict Y from X as well as possible (maximize R 2). To do so, want X variables correlated with Y but not X. Hard to find, e. g. , cognitive ability tests.

Raw & Standardized Regression Weights • Each X has a raw • A b for height in score slope, b. inches would be 12 times larger than b • Slope tells expected for height in feet. change in Y if X changes 1 unit*. • If we standardize X and Y, all units of X • Large b weights are the same. should indicate important variables, • Relative size of b but b depends on now meaningful. variance of X. *strictly speaking, holding other X variables constant.

Computing Standardized Regression Weights Standardized regression weight aka beta weight. Poor choice of names & symbols. With 1 IV, . If you have a correlation matrix, you can calculate beta weights (standardized regression weights). Y x 1 x 2 Y 1 x 1 0. 73 1 x 2 0. 68 0. 64 1 What is r 12? What impact?

2 Calculating R Sum of squared simple (zero order) r. Product of standardized regression weight and r. This is really interesting because the sum of products will add up to R 2 and because r, , and the product of the two are all reasonable indices of the importance of the IV.

2 Calculating R (2) Y x 1 x 2 Y 1 x 1 0. 73 1 x 2 0. 68 0. 64 1

Review • What is the problem with correlated independent variables if we want to maximize variance accounted for in the criterion? • Why do we report beta weights (standardized b weights)? • Describe R-square in two different ways, that is, using two distinct formulas. Explain the formulas.

Tests of Regression Coefficients (b Weights) Each slope tells the expected change in Y when X changes 1 unit, but X is controlled for all other X variables. Consider Venn diagrams. Standard errors of b weights with 2 IVs: Where S 2 y. 12 is the variance of estimate (variance of residuals), the first term in the denominator is the sum of squares for X 1 or X 2, and r 212 is the squared correlation between predictors.

Tests of b Weights (2) SSres=9. 42 For significance of the b weight, compute a t: Degrees of freedom for each t are N-k-1.

2 Tests of R vs Tests of b • Slopes (b) tell about the relation between Y and the unique part of X. R 2 tells about proportion of variance in Y accounted for by set of predictors all together. • Correlations among X variables increase the standard errors of b weights but not R 2. • Possible to get significant R 2, but no or few significant b weights (see Venn diagrams). • Possible but unlikely to have significant b but not significant R 2. Look to R 2 first. If it is n. s. , avoid interpreting b weights.

Review • How is it possible to have a significant R-square and non-significant b weights? • Write a regression equation with beta weights in it. Describe terms.

2 Testing Incremental R You can start regression with a set of one or more variables and then add predictors 1 or more at a time. When you add predictors, R 2 will never go down. It usually goes up, and you can test whether the increment in R 2 is significant or else if likely due to chance. =R-square for the larger model =R-square for the smaller model = number of predictors in the larger model =number of predictors in the smaller model

Examples of Testing Increments Suppose we start with 1 variable and R-square is. 52. We add a second variable and R-square increases to. 67. We have 20 people. Then p<. 05 Suppose we start with 3 IVs and R-square is. 25. We add 2 more IVs in a block and R-square climbs to. 35. We have 100 people. Then: p <. 05

Another Look at Importance • In regression problems, the most commonly used indices of importance are the correlation, r, and the increment to R-square when the variable of interest is considered last. The second is sometimes called a last-in R-square change. The last-in increment corresponds to the Type III sums of squares and is closely related to the b weight. • The correlation tells about the importance of the variable ignoring all other predictors. • The last-in increment tells about the importance of the variable as a unique contributor to the prediction of Y, above and beyond all other predictors in the model. • You can assign shared variance in Y to specific X by adding variable to equations in order, but then the importance is sort of arbitrary and under your influence. • “Importance” is not well defined statistically when IVs are correlated. Doesn’t include mediated models (path analysis).

Review • Find data on website – Labs, then 2 IV example • Find r, beta, r*beta • Describe importance