Regression Statistics 2014 Engineers and Regression Engineers often

Regression Statistics 2014

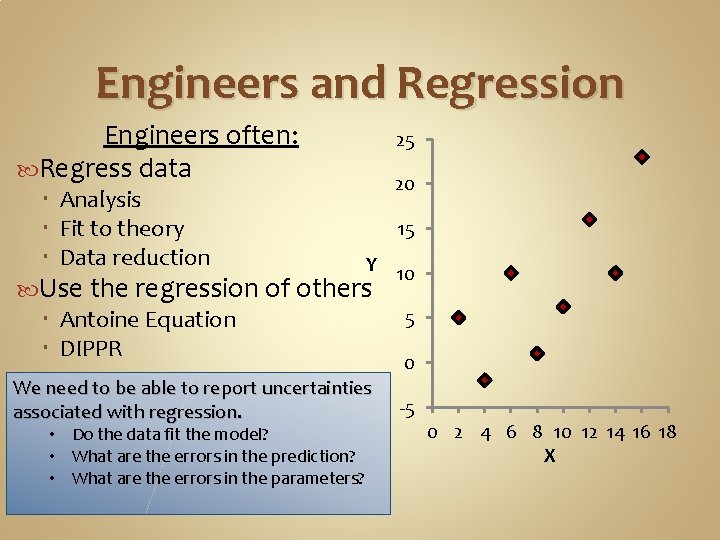
Engineers and Regression Engineers often: Regress data Analysis Fit to theory Data reduction 25 20 15 Y 10 Use the regression of others Antoine Equation DIPPR We need to be able to report uncertainties associated with regression. • Do the data fit the model? • What are the errors in the prediction? • What are the errors in the parameters? 5 0 -5 0 2 4 6 8 10 12 14 16 18 X

Linear Regression There are two classes of regressions Linear Non-linear “Linear” refers to the parameters, not the functional dependence of the independent variable You can use the Mathcad function “linfit” on linear equations

Linear Regression Quiz There are two classes of regressions Linear Non-linear “Linear” refers to the parameters, not the functional dependence of the independent variable You can use the Mathcad function “linfit” on linear equations 1. 2. 3. 4. 5.

Straight Line Model residual (error) 25 20 15 slope Intercept 10 “X” data “Y” Measured “Y” Predicted 5 0 -5 0 2 4 6 8 10 12 14 16 18

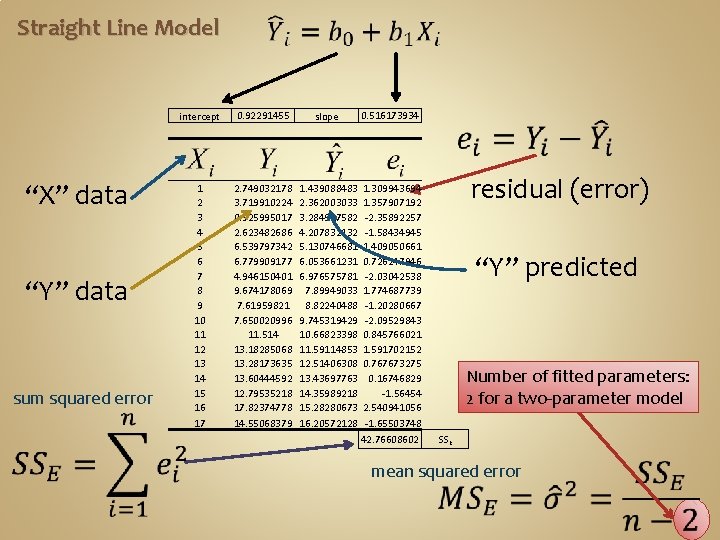
Straight Line Model “X” data “Y” data sum squared error intercept 0. 92291455 slope 0. 516173934 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 2. 749032178 3. 719910224 0. 925995017 2. 623482686 6. 539797342 6. 779909177 4. 946150401 9. 674178069 7. 61959821 7. 650020996 11. 514 13. 18285068 13. 28173635 13. 60444592 12. 79535218 17. 82374778 14. 55068379 1. 439088483 2. 362003033 3. 284917582 4. 207832132 5. 130746681 6. 053661231 6. 976575781 7. 89949033 8. 82240488 9. 745319429 10. 66823398 11. 59114853 12. 51406308 13. 43697763 14. 35989218 15. 28280673 16. 20572128 1. 309943694 1. 357907192 -2. 35892257 -1. 58434945 1. 409050661 0. 726247946 -2. 03042538 1. 774687739 -1. 20280667 -2. 09529843 0. 845766021 1. 591702152 0. 767673275 0. 16746829 -1. 56454 2. 540941056 -1. 65503748 42. 76608602 residual (error) “Y” predicted Number of fitted parameters: 2 for a two-parameter model SSE mean squared error

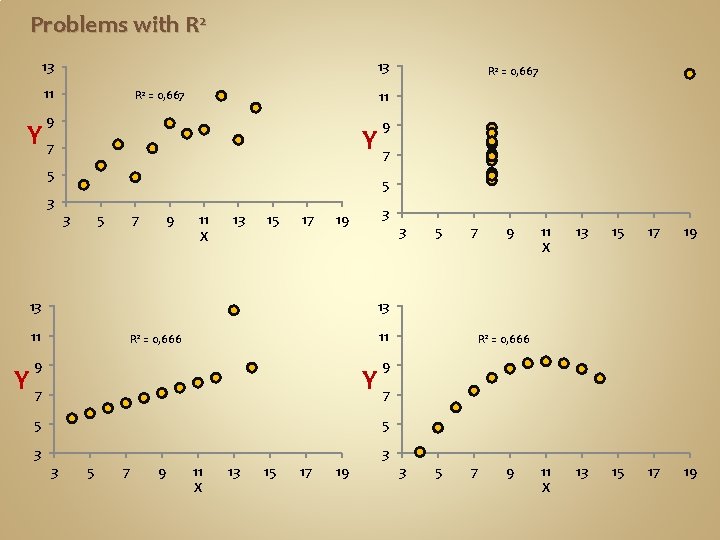
2 The R Statistic A useful statistic but not definitive Tells you how well the data fit the model. It does not tell you if the model is correct. How much of the distribution of the data about the mean is described by the model.

Problems with R 2 13 13 11 R 2 = 0, 667 9 9 Y 7 5 5 3 3 5 7 9 11 X 13 15 17 19 13 11 11 R 2 = 0, 666 9 Y 7 5 5 3 3 R 2 = 0, 666 9 3 5 7 9 11 X 13 15 17 19 3 5 7 9

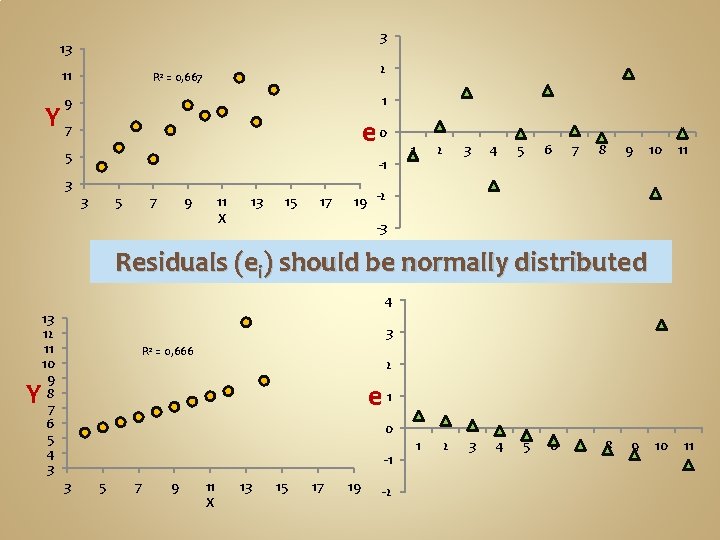
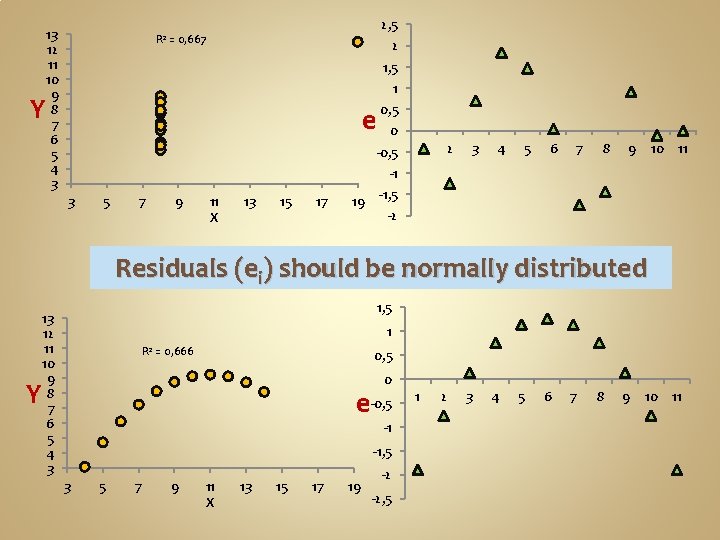
3 13 11 2 R 2 = 0, 667 1 9 Y 7 e 0 5 -1 3 3 5 7 9 11 X 13 15 17 1 2 3 4 5 6 7 8 9 10 11 19 -2 -3 Residuals (ei) should be normally distributed 4 13 12 11 10 9 8 7 6 5 4 3 3 R 2 = 0, 666 2 Y e 1 0 -1 3 5 7 9 11 X 13 15 17 19 -2 1 2 3 4 5 6 7 8 9 10 11

13 12 11 10 9 8 7 6 5 4 3 2, 5 R 2 = 0, 667 2 1, 5 1 Y e 0, 5 0 1 -0, 5 2 3 4 5 6 7 8 9 10 11 -1 3 5 7 9 11 X 13 15 17 19 -1, 5 -2 Residuals (ei) should be normally distributed 1, 5 13 12 11 10 9 8 7 6 5 4 3 1 R 2 = 0, 666 0, 5 0 Y e-0, 5 -1 -1, 5 3 5 7 9 11 X 13 15 17 19 -2 -2, 5 1 2 3 4 5 6 7 8 9 10 11

Other Questions About Fit How well does the line fit the data at each point (not just the mean)? In what range should the data lie (are there outliers)? What are the confidence intervals on the slope and intercept?

Confidence Intervals from Example Green is confidence interval How well does the model fit the data? Red is the prediction band Where should the data fall? Can I throw out any points?

Statistics on the Slope/Intercept When you fit data to a straight line, the slope and intercept are only estimates of the true slope and intercept. (1 -a)100% Confidence Intervals (slope) (intercept) Standard Errors

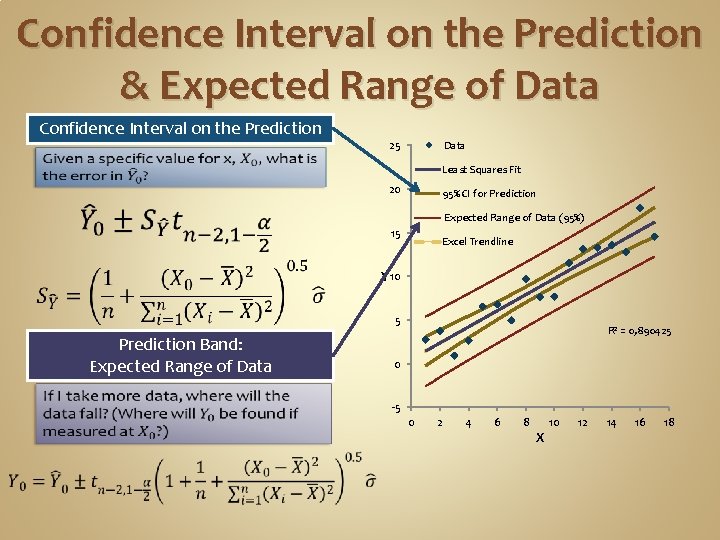
Confidence Interval on the Prediction & Expected Range of Data Confidence Interval on the Prediction 25 Data Least Squares Fit 20 95% CI for Prediction Expected Range of Data (95%) 15 Excel Trendline Y 10 5 Prediction Band: Expected Range of Data R 2 = 0, 890425 0 -5 0 2 4 6 8 X 10 12 14 16 18

Confidence Interval vs. Prediction Band CONFIDENCE INTERVAL “Mean Prediction Band” Shows possible errors in where the line will go Interval narrows with increasing number of data points See equation on previous slide PREDICTION BAND “Single (another) Point Prediction Band” Shows where the data should lie Interval does not narrow much with increasing number of data points See equation on previous slide

Good News: IGOR! Igor has the equations already programmed and will • Plot the confidence intervals • Plot the prediction bands • Print the confidence intervals on the slope and intercept Assignment

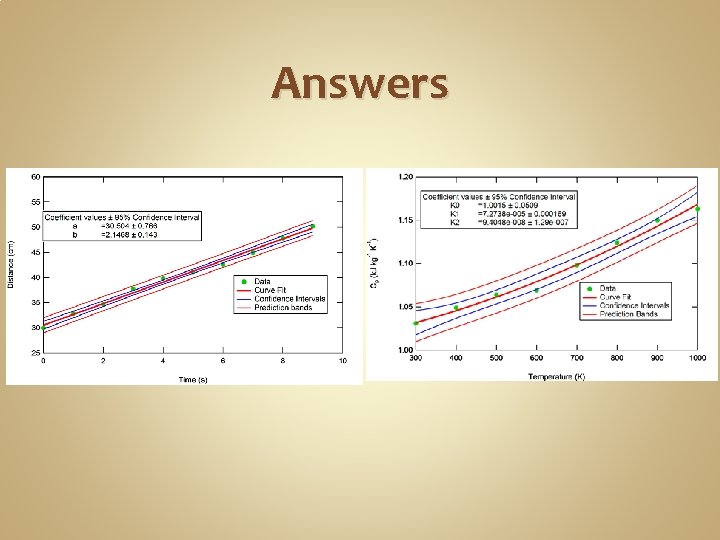
Answers

Example Using Excel

Generalized Linear Regression Linear regression can be written in matrix form. X 21 24 32 47 50 59 68 74 62 50 41 30 Y 186 214 288 425 455 539 622 675 562 453 370 274 Straight Line Model Quadratic Model

Statistics with Matrices Parameter Confidence Intervals Standard Error of bi is the square root of the i-th diagonal term of the matrix Predicted Variable Confidence Intervals