Regression classification and clustering interpreting and exploring data

Regression, classification and clustering - interpreting and exploring data Peter Fox Data Analytics – ITWS-4600/ITWS-6600/MATP-4450 Group 2, Module 5, February 5, 2018 1

Regression • Retrieve this dataset: dataset_multiple. Regression. csv • Using the unemployment rate (UNEM) and number of spring high school graduates (HGRAD), predict the fall enrollment (ROLL) for this year by knowing that UNEM=9% and HGRAD=100, 000. • Repeat and add per capita income (INC) to the model. Predict ROLL if INC=$30, 000 • Summarize and compare the two models. • Comment on significance 2

Object of class lm: An object of class "lm" is a list containing at least the following components: coefficients a named vector of coefficients residuals the residuals, that is response minus fitted values. fitted. values the fitted mean values. rank the numeric rank of the fitted linear model. weights (only for weighted fits) the specified weights. df. residual the residual degrees of freedom. call the matched call. terms the terms object used. contrasts (only where relevant) the contrasts used. xlevels (only where relevant) a record of the levels of the factors used in fitting. offset the offset used (missing if none were used). y if requested, the response used. x if requested, the model matrix used. model if requested (the default), the model frame used. 3

Regression Exercises (lab 2) • Using the EPI dataset find the single most important factor in increasing the EPI in a given region • Examine distributions across all the columns and build up an EPI “model” • We will be interpreting and discussing these models next module (week)! 4

Classification • abalone. csv dataset = predicting the age of abalone from physical measurements. • The age of abalone is determined by cutting the shell through the cone, staining it, and counting the number of rings through a microscope: a boring and time-consuming task. • Other measurements, which are easier to obtain, are used to predict the age. • Perform knn classification to get predictors for Age (Rings). 5

Clustering • The Iris dataset (in R use data(“iris”) to load it) • The 5 th column is the species and you want to find how many clusters without using that information • Create a new data frame and remove the fifth column • Apply kmeans (you choose k) with 1000 iterations • Use table(iris[, 5], <your clustering>) to assess results 6

Return object cluster A vector of integers (from 1: k) indicating the cluster to which each point is allocated. centers A matrix of cluster centres. totss The total sum of squares. withinss Vector of within-cluster sum of squares, one component per cluster. tot. withinss Total within-cluster sum of squares, i. e. , sum(withinss). betweenss The between-cluster sum of squares, i. e. totss-tot. withinss. size The number of points in each cluster. 7

K-Means Algorithm: Example Output

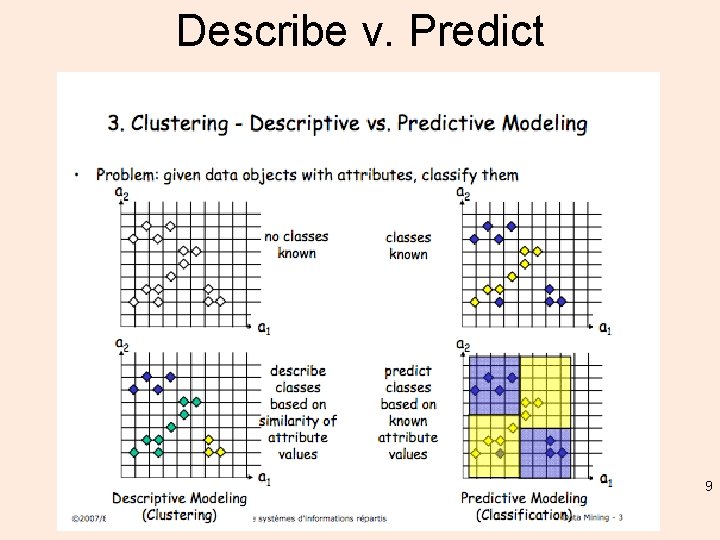
Describe v. Predict 9

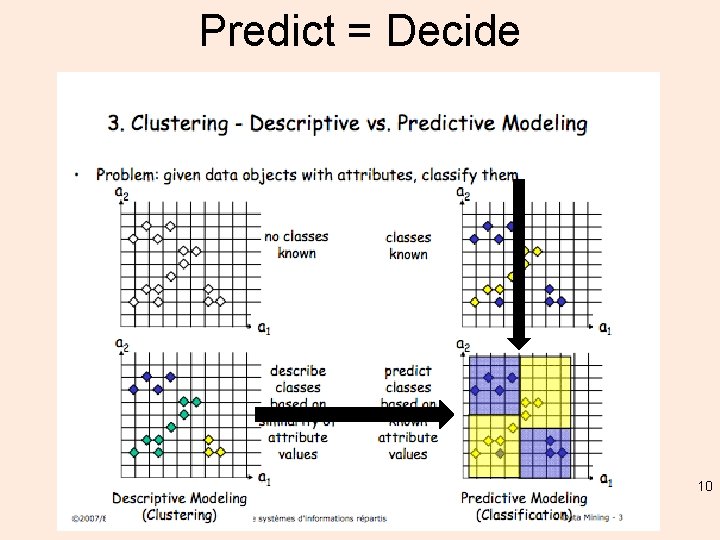
Predict = Decide 10

Contingency table 11

Classification or clustering on nyt dataset(s) "Age", "Gender", "Impressions", "Clicks", "Signed_In" 36, 0, 3, 0, 1 73, 1, 3, 0, 1 30, 0, 3, 0, 1 49, 1, 3, 0, 1 47, 1, 11, 0, 1 47, 0, 11, 1, 1 (nyt datasets) Model e. g. : If Age<45 and Impressions >5 then Gender=female (0) Age ranges? 41 -45, 46 -50, etc? 12

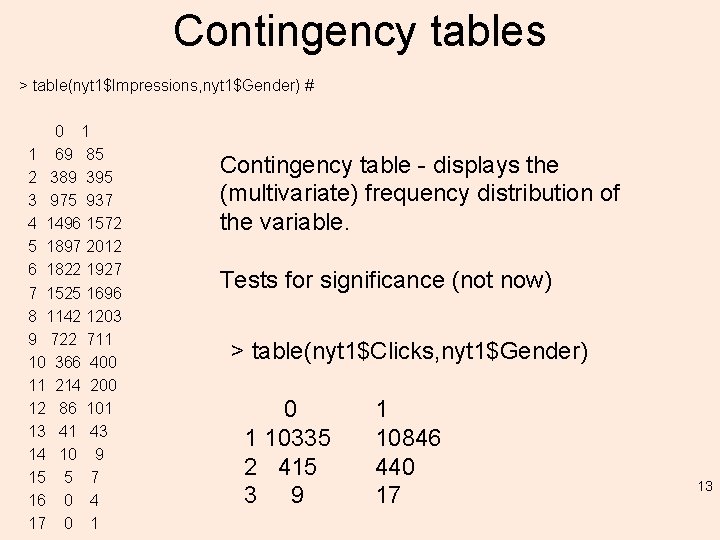
Contingency tables > table(nyt 1$Impressions, nyt 1$Gender) # 0 1 1 69 85 2 389 395 3 975 937 4 1496 1572 5 1897 2012 6 1822 1927 7 1525 1696 8 1142 1203 9 722 711 10 366 400 11 214 200 12 86 101 13 41 43 14 10 9 15 5 7 16 0 4 17 0 1 Contingency table - displays the (multivariate) frequency distribution of the variable. Tests for significance (not now) > table(nyt 1$Clicks, nyt 1$Gender) 0 1 10335 2 415 3 9 1 10846 440 17 13

Classification Exercises (group 1/lab 2_knn 1. R) > nyt 1<-read. csv(“nyt 1. csv") > nyt 1<-nyt 1[which(nyt 1$Impressions>0 & nyt 1$Clicks>0 & nyt 1$Age>0), ] > nnyt 1<-dim(nyt 1)[1] # shrink it down! > sampling. rate=0. 9 > num. test. set. labels=nnyt 1*(1. -sampling. rate) > training <-sample(1: nnyt 1, sampling. rate*nnyt 1, replace=FALSE) > train<-subset(nyt 1[training, ], select=c(Age, Impressions)) > testing<-setdiff(1: nnyt 1, training) > test<-subset(nyt 1[testing, ], select=c(Age, Impressions)) > cg<-nyt 1$Gender[training] > true. labels<-nyt 1$Gender[testing] > classif<-knn(train, test, cg, k=5) # > classif > attributes(. Last. value) # interpretation to come! 14

K Nearest Neighbors (classification) > nyt 1<-read. csv(“nyt 1. csv") … from week 3 lab slides or scripts > classif<-knn(train, test, cg, k=5) # > head(true. labels) [1] 1 0 0 1 1 0 > head(classif) [1] 1 1 0 0 Levels: 0 1 > ncorrect<-true. labels==classif > table(ncorrect)["TRUE"] # or > length(which(ncorrect)) > What do you conclude? 15

Weighted KNN… require(kknn) data(iris) m <- dim(iris)[1] val <- sample(1: m, size = round(m/3), replace = FALSE, prob = rep(1/m, m)) iris. learn <- iris[-val, ] iris. valid <- iris[val, ] iris. kknn <- kknn(Species~. , iris. learn, iris. valid, distance = 1, kernel = "triangular") summary(iris. kknn) fit <- fitted(iris. kknn) table(iris. valid$Species, fit) pcol <- as. character(as. numeric(iris. valid$Species)) pairs(iris. valid[1: 4], pch = pcol, col = c("green 3", "red”)[(iris. valid$Species != fit)+1]) 16

summary Call: kknn(formula = Species ~. , train = iris. learn, test = iris. valid, "triangular") Response: "nominal" fit prob. setosa prob. versicolor prob. virginica 1 versicolor 0 1. 0000 0. 0000 2 versicolor 0 1. 0000 0. 0000 3 versicolor 0 0. 91553003 0. 08446997 4 setosa 1 0. 00000000 5 virginica 0 0. 0000 1. 0000 6 virginica 0 0. 0000 1. 0000 7 setosa 1 0. 00000000 8 versicolor 0 0. 66860033 0. 33139967 9 virginica 0 0. 22534461 0. 77465539 10 versicolor 0 0. 79921042 0. 20078958 11 virginica 0 0. 00000000 12. . . distance = 1, kernel = 17

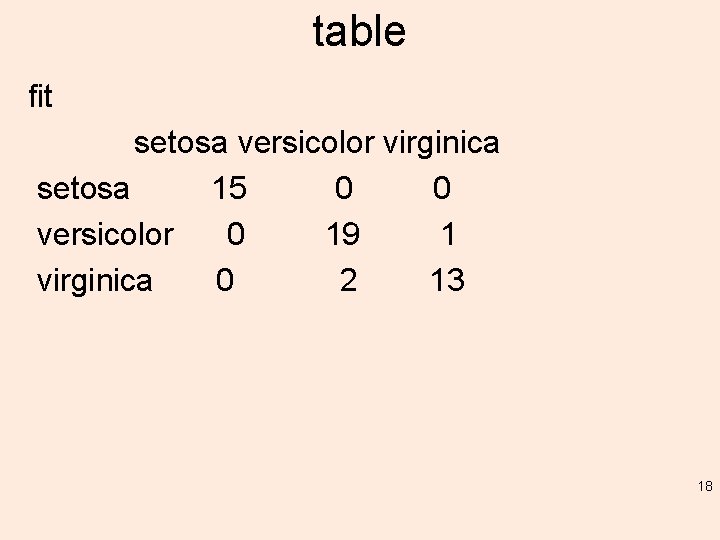
table fit setosa versicolor virginica setosa 15 0 0 versicolor 0 19 1 virginica 0 2 13 18

pcol <- as. character(as. numeric(iris. valid$Species)) pairs(iris. valid[1: 4], pch = pcol, col = c("green 3", "red”)[(iris. valid$Species != fit)+1]) 19

Ctrees? • We want a means to make decisions – so how about a “if this then this otherwise that” approach == tree methods, or branching. • Conditional Inference – what is that? • Instead of: if (This 1. and. This 2. and. This 3. and. …) 20

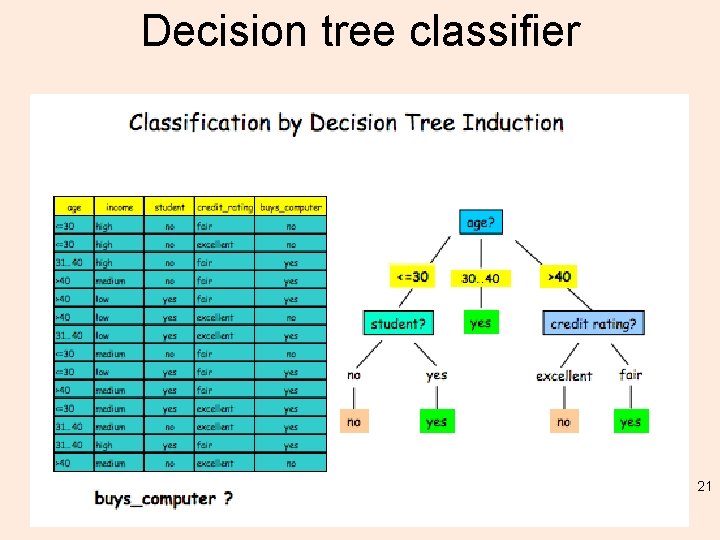
Decision tree classifier 21

Conditional Inference Tree > require(party) # don’t get me started! > str(iris) 'data. frame': 150 obs. of 5 variables: $ Sepal. Length: num 5. 1 4. 9 4. 7 4. 6 5 5. 4 4. 6 5 4. 4 4. 9. . . $ Sepal. Width : num 3. 5 3 3. 2 3. 1 3. 6 3. 9 3. 4 2. 9 3. 1. . . $ Petal. Length: num 1. 4 1. 3 1. 5 1. 4 1. 7 1. 4 1. 5. . . $ Petal. Width : num 0. 2 0. 4 0. 3 0. 2 0. 1. . . $ Species : Factor w/ 3 levels "setosa", "versicolor", . . : 1 1 1 1 1. . . > iris_ctree <- ctree(Species ~ Sepal. Length + Sepal. Width + Petal. Length + Petal. Width, data=iris) 22

Ctree > print(iris_ctree) Conditional inference tree with 4 terminal nodes Response: Species Inputs: Sepal. Length, Sepal. Width, Petal. Length, Petal. Width Number of observations: 150 1) Petal. Length <= 1. 9; criterion = 1, statistic = 140. 264 2)* weights = 50 1) Petal. Length > 1. 9 3) Petal. Width <= 1. 7; criterion = 1, statistic = 67. 894 4) Petal. Length <= 4. 8; criterion = 0. 999, statistic = 13. 865 5)* weights = 46 4) Petal. Length > 4. 8 6)* weights = 8 3) Petal. Width > 1. 7 7)* weights = 46 23

plot(iris_ctree) 24 > plot(iris_ctree, type="simple”) # try this

Beyond plot: pairs(iris[1: 4], main = "Anderson's Iris Data -- 3 species”, pch = 21, bg = c("red", "green 3", "blue")[unclass(iris$Species)]) 25

But the means for branching. . • Do not have to be threshold based ( ~ distance) • Can be cluster based = I am more similar to you if I possess these attributes (in this range) • Thus: trees + cluster = hierarchical clustering • In R: hclust (and others) in stats package 26

Try hclust for iris 27

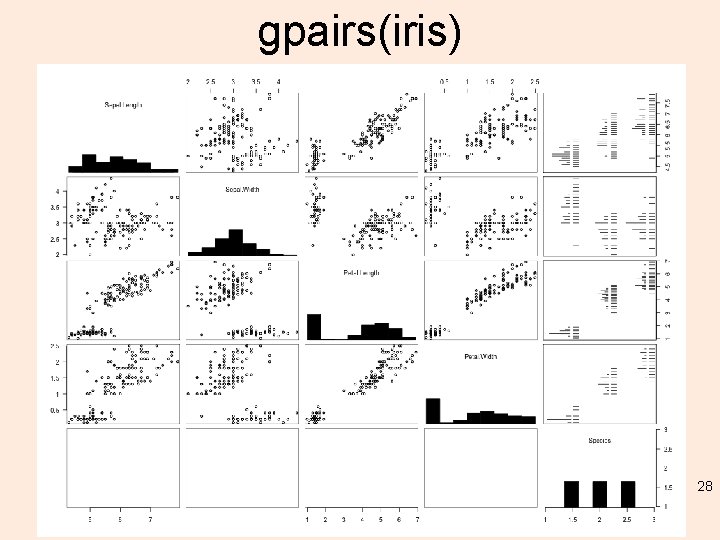
gpairs(iris) 28

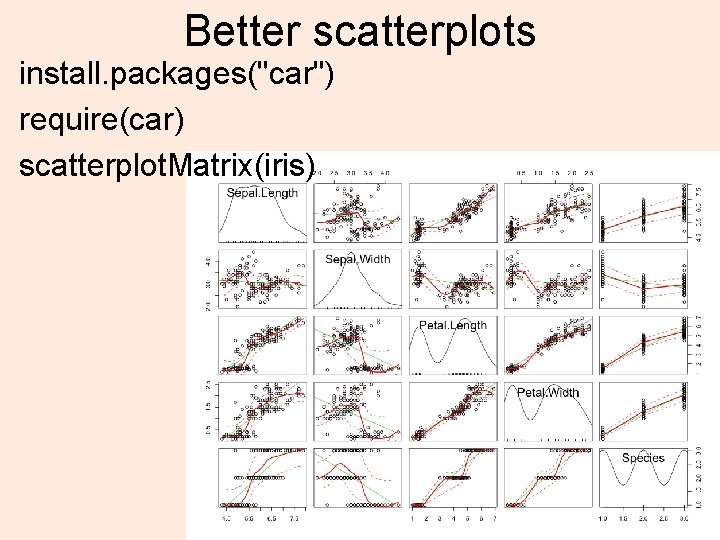
Better scatterplots install. packages("car") require(car) scatterplot. Matrix(iris) 29

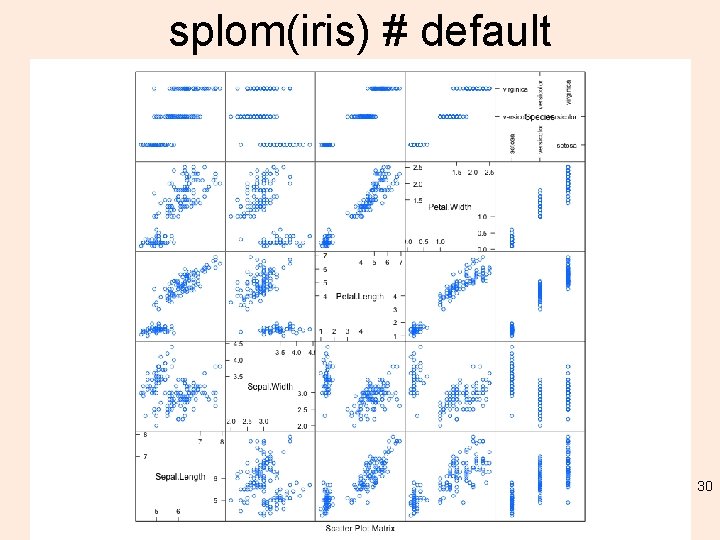
splom(iris) # default 30

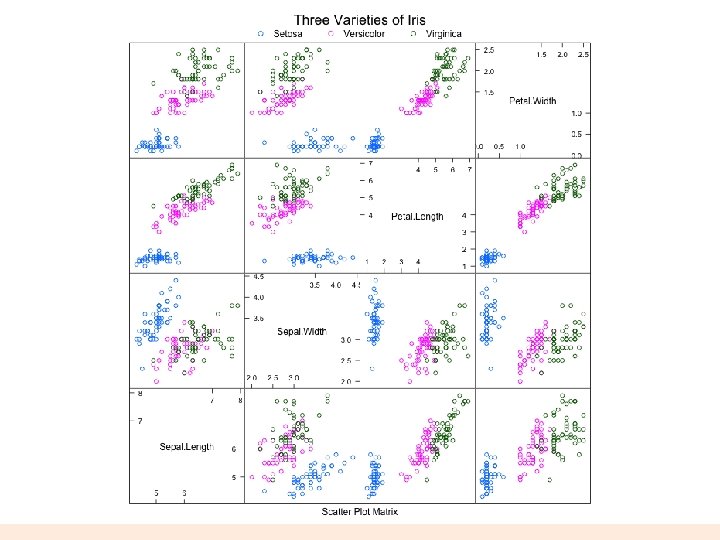
splom extra! require(lattice) super. sym <- trellis. par. get("superpose. symbol") splom(~iris[1: 4], groups = Species, data = iris, panel = panel. superpose, key = list(title = "Three Varieties of Iris", columns = 3, points = list(pch = super. sym$pch[1: 3], col = super. sym$col[1: 3]), text = list(c("Setosa", "Versicolor", "Virginica")))) splom(~iris[1: 3]|Species, data = iris, layout=c(2, 2), pscales = 0, varnames = c("Sepaln. Length", "Sepaln. Width", "Petaln. Length"), page = function(. . . ) { ltext(x = seq(. 6, . 8, length. out = 4), y = seq(. 9, . 6, length. out = 4), labels = c("Three", "Varieties", "of", "Iris"), cex = 2) }) parallelplot(~iris[1: 4] | Species, iris) parallelplot(~iris[1: 4], iris, groups = Species, horizontal. axis = FALSE, scales = list(x = list(rot = 90))) 31

32

33

Shift the dataset… 34

Hierarchical clustering > d <- dist(as. matrix(mtcars)) > hc <- hclust(d) > plot(hc) 35

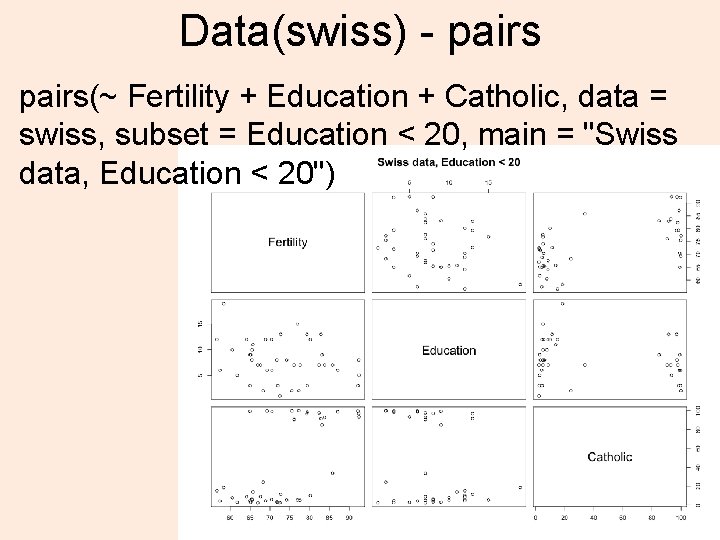
Data(swiss) - pairs(~ Fertility + Education + Catholic, data = swiss, subset = Education < 20, main = "Swiss data, Education < 20") 36

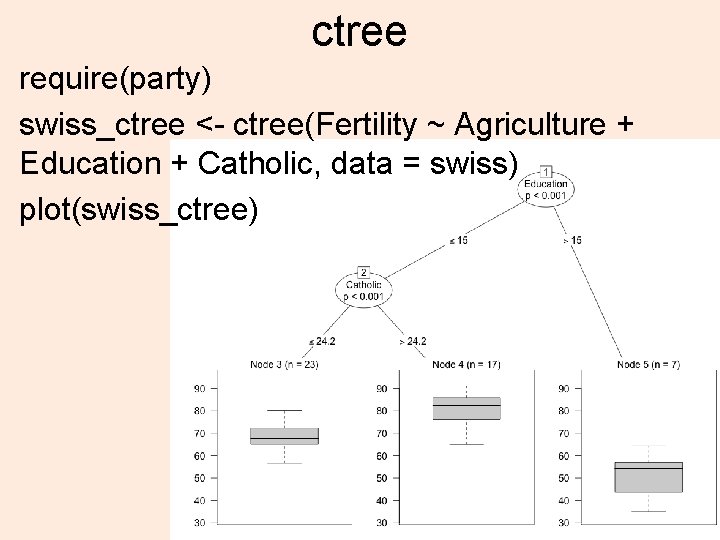
ctree require(party) swiss_ctree <- ctree(Fertility ~ Agriculture + Education + Catholic, data = swiss) plot(swiss_ctree) 37

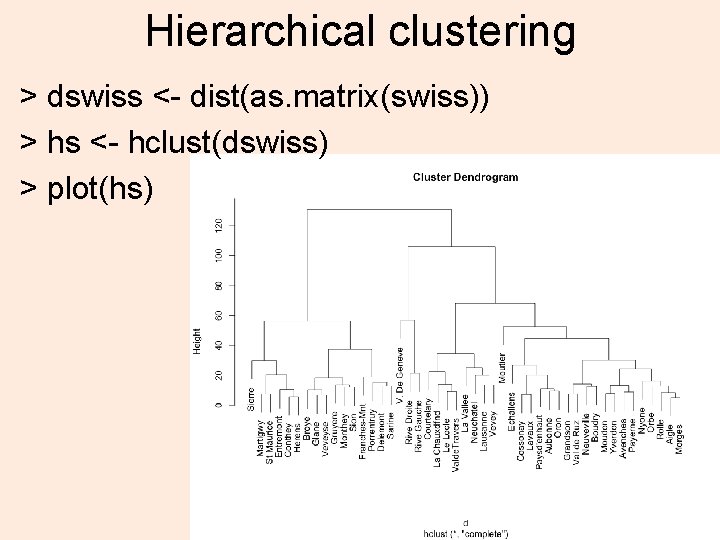
Hierarchical clustering > dswiss <- dist(as. matrix(swiss)) > hs <- hclust(dswiss) > plot(hs) 38

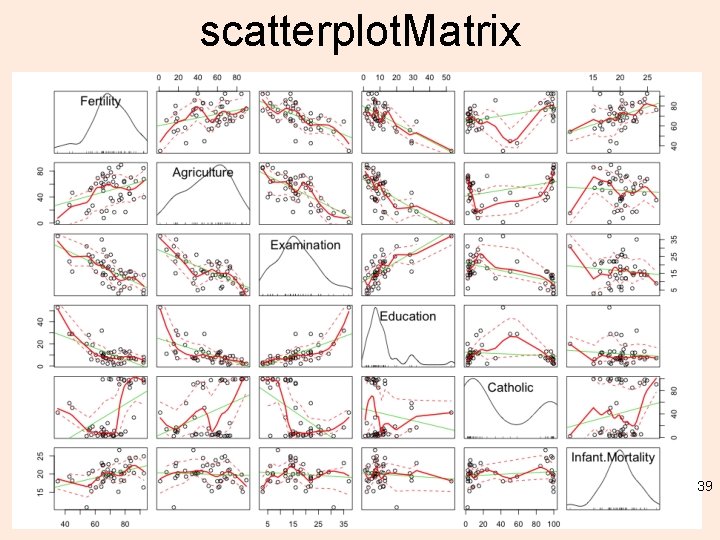
scatterplot. Matrix 39

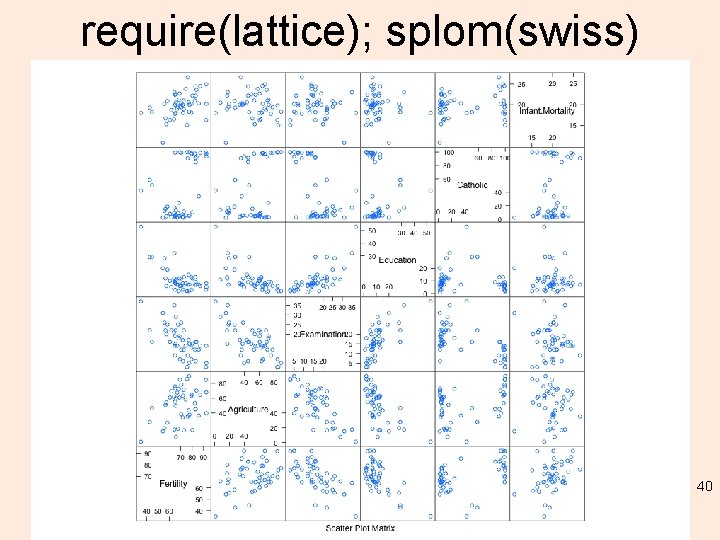
require(lattice); splom(swiss) 40

Start collecting • Your favorite plotting routines • Get familiar with annotating plots 41

Assignment 3 • Preliminary and Statistical Analysis. Due February 23. 15% (written) – Distribution analysis and comparison, visual ‘analysis’, statistical model fitting and testing of some of the nyt 2… 31 datasets. – See LMS … for Assignment and details. 42